Похожие презентации:
Формула полной вероятности
1.
Формула полной вероятности являетсяследствием теорем о сложении и умножении
вероятностей.
Пусть требуется определить вероятность
события А, которое может произойти только
вместе с одним из событий Н1,Н2…Нn
образующих полную группу несовместных
событий.
Эти события называются гипотезами.
2.
Так как гипотезы образуют полную группу, тособытие А может появиться только в комбинации
с одной из этих гипотез. Поэтому,
А H1 A H 2 A ... H n A
Так как гипотезы Н1,Н2…Нn несовместны, то и
комбинации Н1А, Н2А … НnА тоже несовместны.
Тогда по теореме о сложении вероятностей
n
P( А) P( H1 A) P( H 2 A) ... P( H n A) P( H i A)
i 1
По теореме об умножении вероятностей
P( H i A) P( H i ) P( A | H i )
Отсюда вытекает формула полной вероятности:
3.
nP( A) P( H i ) P( A | H i )
i 1
4.
Студент, выйдя из дома за 30 минут доначала занятий, может приехать
в институт автобусом, троллейбусом или
трамваем. Все эти варианты равновозможны.
Вероятность приехать на занятия вовремя
для этих видов транспорта соответственно
равна 0.99, 0.98 и 0.9. Какова вероятность,
что студент приедет на учебу вовремя?
5.
Пусть событие А заключается в том, что студентне опоздает на занятия. Оно может произойти
только вместе с одной из гипотез:
Н1- студент поехал автобусом;
Н2- студент поехал троллейбусом;
Н3- студент поехал трамваем.
Чтобы использовать формулу полной вероятности,
необходимо знать вероятности каждой из гипотез
и условные вероятности события А для каждой
из гипотез.
6.
Так как гипотезы образуют полную группу событий, тосуммарная вероятность всех гипотез равна 1.
По условию задачи
следовательно
все
гипотезы
равновероятны,
Р(Н1)=Р(Н2)=Р(Н3)=1/3.
1 – в числителе обозначает, что взят один из видов
транспорта;
3 – в знаменателе означает, что всего три вида
транспорта
Условные вероятности события А для каждой из гипотез
даны по условию задачи:
Р(А|Н1)=0.99; Р(А|Н2)=0.98; Р(А|Н3)=0.9
Следовательно, по формуле полной вероятности,
7.
11
1
P( A) 0.99 0.98 0.9 0.96
3
3
3
8.
На сборку поступают однотипные изделия из четырехцехов.
Вероятности
изготовления
бракованного
изделия первым, вторым, третьим и четвертым цехами
соответственно равны 0,03; 0,01; 0,02; 0,01. Какова
вероятность того, что взятое на удачу изделие окажется
бракованным?






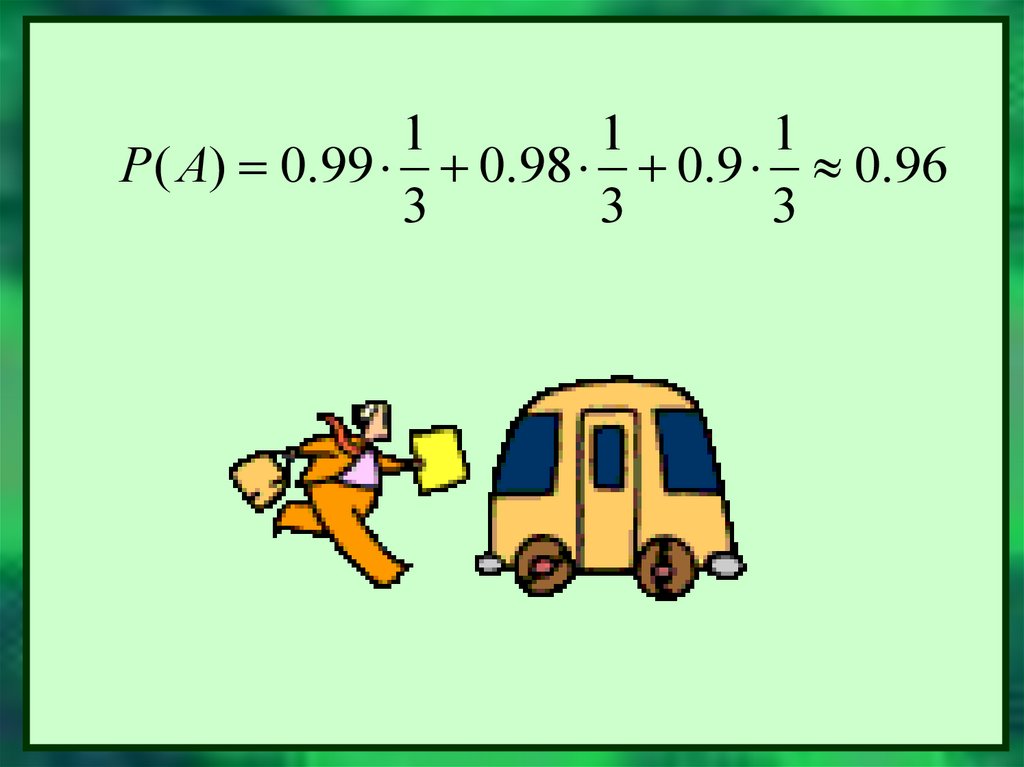

 Математика
Математика








