Похожие презентации:
Формула полной вероятности
1.
Формула полной вероятности являетсяследствием теорем о сложении и умножении
вероятностей.
Пусть требуется определить вероятность
события А, которое может произойти только
вместе с одним из событий Н1,Н2…Нn
образующих полную группу несовместных
событий.
Эти события называются гипотезами.
2.
Студент, выйдя из дома за 30 минут доначала занятий, может приехать
в институт автобусом, троллейбусом или
трамваем. Все эти варианты равновозможны.
Вероятность приехать на занятия вовремя
для этих видов транспорта соответственно
равна 0.99, 0.98 и 0.9. Какова вероятность,
что студент приедет на учебу вовремя?
3.
Пусть событие А заключается в том, что студентне опоздает на занятия. Оно может произойти
только вместе с одной из гипотез:
Н1- студент поехал автобусом;
Н2- студент поехал троллейбусом;
Н3- студент поехал трамваем.
4.
Так как гипотезы образуют полную группу, тособытие А может появиться только в комбинации
с одной из этих гипотез. Поэтому,
А H1 A H 2 A ... H n A
n
P( А) P( H1 A) P( H 2 A) ... P( H n A) P( H i A)
i 1
По теореме об умножении вероятностей
P( H i A) P( H i ) P( A | H i )
Отсюда вытекает формула полной вероятности:
5.
Так как гипотезы образуют полную группу, тособытие А может появиться только в комбинации
с одной из этих гипотез. Поэтому,
А H1 A H 2 A ... H n A
Так как гипотезы Н1,Н2…Нn несовместны, то и
комбинации Н1А, Н2А … НnА тоже несовместны.
Тогда по теореме о сложении вероятностей
n
P( А) P( H1 A) P( H 2 A) ... P( H n A) P( H i A)
P( À) P( H1 A) P( H 2 A) ... P( Hi n1 A)
По теореме об умножении вероятностей
P( H i A) P( H i ) P( A | H i )
Отсюда вытекает формула полной вероятности:
6.
Так как гипотезы образуют полную группу, тособытие А может появиться только в комбинации
с одной из этих гипотез. Поэтому,
А H1 A H 2 A ... H n A
Так как гипотезы Н1,Н2…Нn несовместны, то и
комбинации Н1А, Н2А … НnА тоже несовместны.
Тогда по теореме о сложении вероятностей
n
P( А) P( H1 A) P( H 2 A) ... P( H n A) P( H i A)
P( À) P( H1 A) P( H 2 A) ... P( H n A)
P( A / H1 ) P( H1 ) P( A / H 2 ) P( H 2 )
P( A / iH
) P( H n )
1n
По теореме об умножении вероятностей
P( H i A) P( H i ) P( A | H i )
Отсюда вытекает формула полной вероятности:
7.
nP( A) P( A | H i ) P( H i )
i 1
8.
Студент, выйдя из дома за 30 минут доначала занятий, может приехать
в институт автобусом, троллейбусом или
трамваем. Все эти варианты равновозможны.
Вероятность приехать на занятия вовремя
для этих видов транспорта соответственно
равна 0.99, 0.98 и 0.9. Какова вероятность,
что студент приедет на учебу вовремя?
9.
Пусть событие А заключается в том, что студентне опоздает на занятия. Оно может произойти
только вместе с одной из гипотез:
Н1- студент поехал автобусом;
Н2- студент поехал троллейбусом;
Н3- студент поехал трамваем.
Чтобы использовать формулу полной вероятности,
необходимо знать вероятности каждой из гипотез
и условные вероятности события А для каждой
из гипотез.
10.
Так как гипотезы образуют полную группусобытий, то суммарная вероятность всех гипотез
равна 1.
По условию задачи все гипотезы равновероятны,
следовательно
Р(Н1)=Р(Н2)=Р(Н3)=1/3.
Условные вероятности события А для каждой из
гипотез даны по условию задачи:
Р(А|Н1)=0.99; Р(А|Н2)=0.98; Р(А|Н3)=0.9
Следовательно, по формуле полной вероятности,
11.
11
1
P( A) 0.99 0.98 0.9 0.96
3
3
3
12.
В магазин изделия пост авляют ся т ремя фирмами.Извест но, чт о первая фирма пост авляет т овар
с браком в 0,1%, вт орая – 0,15%, т рет ья – 0,25%.
С первой фирмы пост упило 500,
со вт орой – 200, а с т рет ьей – 300 изделий.
Найт и вероят ност ь, чт о приобрет ённое изделие
окажет ся
а) ст андарт ным;
б) нест андарт ным;
13.
При переливании крови надо учитывать группукрови донора т больного. Человеку, имеющему
четвертую группу, можно перелить кровь
любой группы; человеку со второй
или третьей группой можно перелить кровь
либо той же группы, либо первой;
человеку с первой группой можно
перелить только кровь его группы.
Среди населения 33.7%, имеют первую, 37,5% - вторую,
20,9% - третью и 7,9% - четвертую группу крови.
Найти вероятность того, что случайно взятому
больному можно перелить кровь случайно взятого
донора.
14.
33.7% I37,5% - II
20,9% - III
7,9% - IV
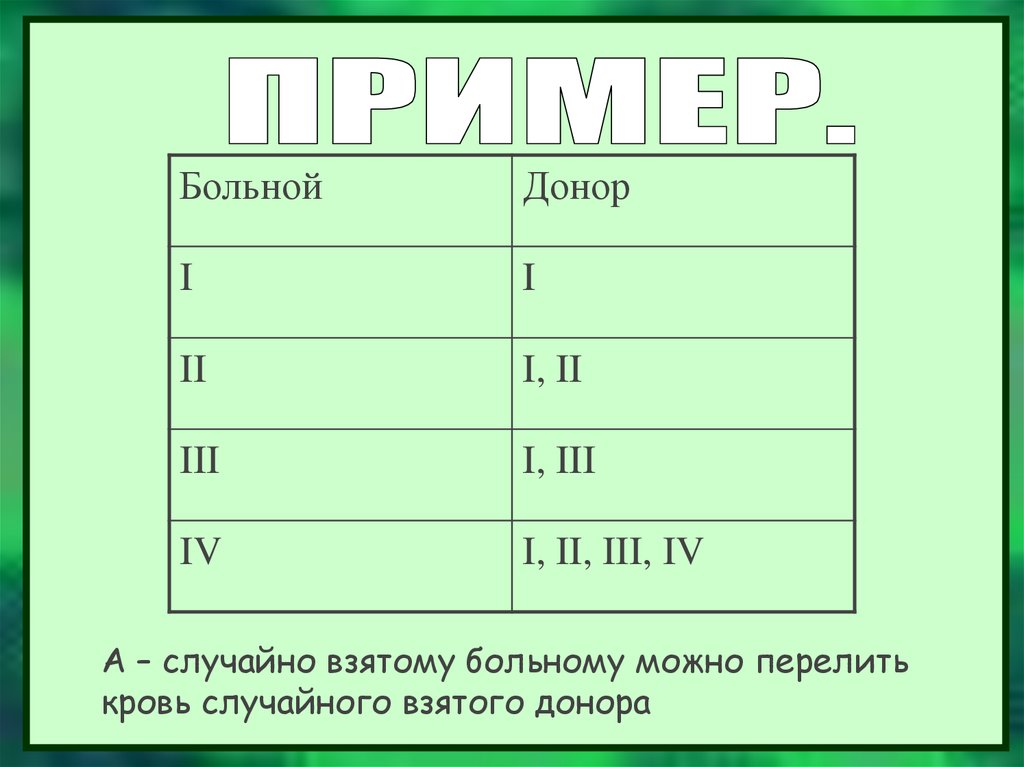
15.
БольнойДонор
I
I
II
I, II
III
I, III
IV
I, II, III, IV
А – случайно взятому больному можно перелить
кровь случайного взятого донора
16.
А – случайно взятому больному можно перелитькровь случайного взятого донора
P(A)=0,57










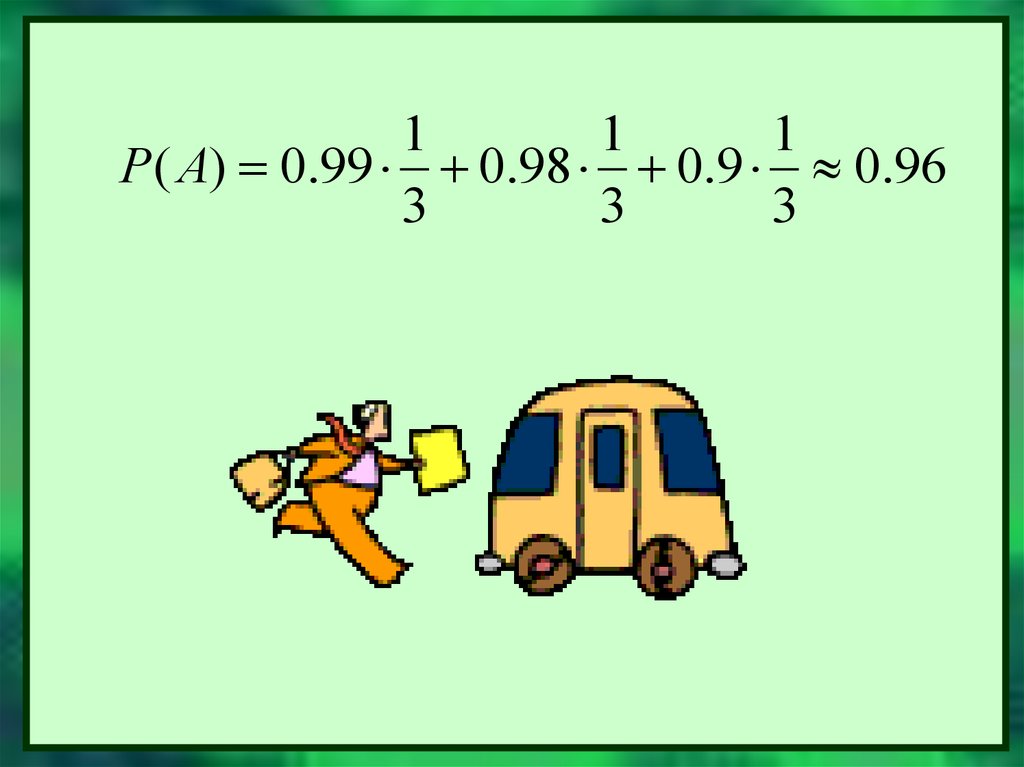




 Математика
Математика








