Формула полной вероятности

1. Умножение вероятностей

ПОВТОРЕНИЕ
29 октября 2020 г.

2. Формула умножения вероятностей

Для независимых событий
Для зависимых событий
P( AB) P( A) P( B)
P( AB) P( A) P( B / A)
Последняя формула учитывает изменение вероятности второго
события после того, как произошло первое.
Иванов О.В., Соколихин А.А. 2005
2

3. Задачка 1

Вероятность попадания в мишень для первого стрелка 0,8, а
для второго – 0,6. Стрелки независимо друг от друга сделают
по одному выстрелу.
а). Какова вероятность того, что в мишень попадут оба
стрелка?
б). Какова вероятность того, что в мишень попадет хотя бы
один из стрелков?
Иванов О.В., Соколихин А.А. 2005
3

4. Задачка 2

В команде из 12 спортсменов 5 мастеров спорта. По
жеребьевке из команды выбирают 3-х спортсменов. Какова
вероятность того, что все выбранные спортсмены являются
мастерами спорта?
Иванов О.В., Соколихин А.А. 2005
4

5. Задачка 3

Имеется три ящика, в каждом из которых лежат шары с
номерами от 0 до 9. Из каждого ящика вынимается по одному
шару. Какова вероятность того, что
а) вынуты три девятки;
б) вынуты три одинаковых числа?
Иванов О.В., Соколихин А.А. 2005
5

6. Формула полной вероятности

Объяснение формулы
Примеры
29 октября 2020 г.

7. Формула полной вероятности

Применяется, когда опыт со случайными исходами распадается
на два случая:
розыгрыш условий опыта
розыгрыш результата
Иванов О.В., Соколихин А.А. 2005
7
7

8. Пример1

Имеются два одинаковых ящика с карандашами. В 1-ом
ящике – 2 зеленых и 1 синий карандаш, во 2-ом – 1
зеленый и 3 синих. Наудачу выбирают один из ящиков и
вынимают из него карандаш. Какова вероятность вынуть
зеленый карандаш?
Иванов О.В., Соколихин А.А. 2005
8
8

9. Терминология

Допустим, что об условиях опыта можно сделать n
исключающих
друг
друга
предположений
(гипотез):
H1,H2,…,Hn, где Hi Hj = Ø, i ≠ j
n
H
i 1
i
Hi – несовместные, образующие полную группу
события.
Иванов О.В., Соколихин А.А. 2005
9
9

10. Формула полной вероятности

Заданы условные вероятности события А, при
каждой из гипотез P(A‫׀‬H1),…,P(A‫׀‬Hn). Событие А
может появиться только вместе с одной из
гипотез.
Найдем вероятность события А.
A= H1A +H2A + …+ HnA , HiA – несовместные
n,
события, значит
P ( H i A)
P(HiA) = P(Hi)∙P(A‫׀‬Hi) P ( A)
n
P ( A) P ( H i )P ( A | H i )
Отсюда
i 1
вероятности
Иванов О.В., Соколихин А.А. 2005
i 1
– формула полной
10
10

11. Формула полной вероятности

Если события H1 и H2 образуют полную группу событий,
вероятность случайного события А находится по формуле
полной вероятности:
P( A) P( H1 ) P( A / H1 ) P( H 2 ) P( A / H 2 )
E
A
H1
Иванов О.В., Соколихин А.А. 2005
H2
11

12. Формула полной вероятности

Если полная группа включает n событий, тогда формула полной
вероятности имеет следующий вид:
P( A) P( H1 ) P( A / H1 ) ... P( H n ) P( A / H n )
E
A
H1
Иванов О.В., Соколихин А.А. 2005
H2
H3
…
Hn
12

13. Пример1

Имеются два одинаковых ящика с карандашами. В 1-ом ящике –
2 зеленых и 1 синий карандаш, во 2-ом – 1 зеленый и 3
синих. Наудачу выбирают один из ящиков и вынимают из
него карандаш. Какова вероятность вынуть зеленый
карандаш?
Иванов О.В., Соколихин А.А. 2005
13
13

14. Решение

Hi – выбор i ящика
P(H1) = P(H2)=1/2
P(A‫׀‬H1) =2/3
P(A‫׀‬H2) = ¼
P( A) P( H1 ) P( A / H1 ) P( H 2 ) P( A / H 2 )
1 2 1 1 1 8 3 11
р ( А)
2 3 2 4 2 12 24
Иванов О.В., Соколихин А.А. 2005
14
14

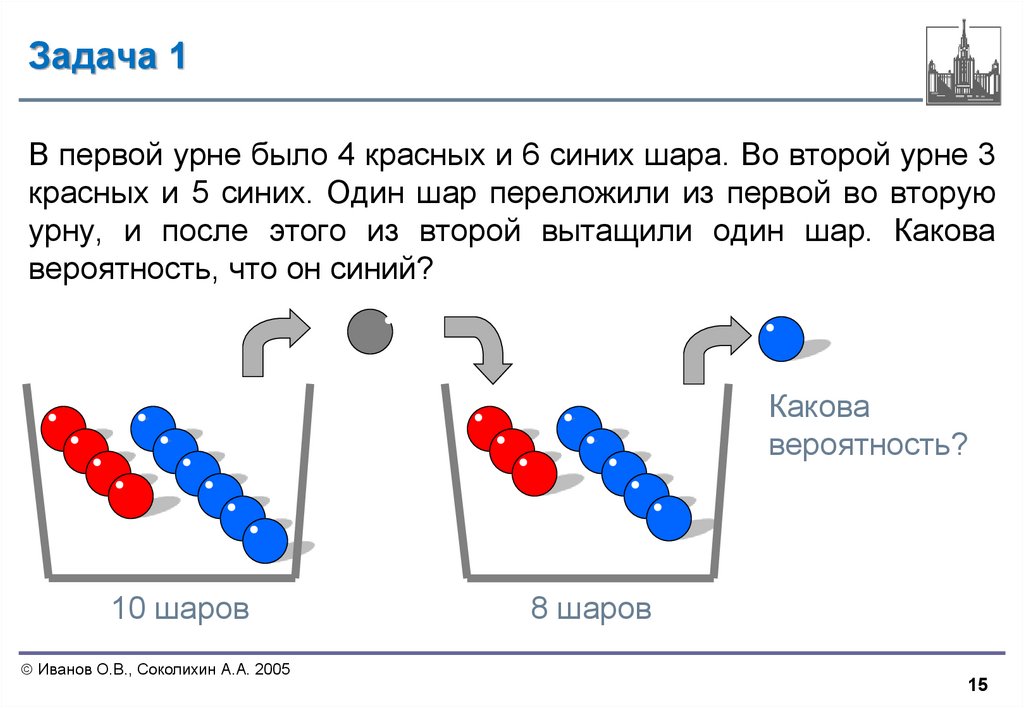
15. Задача 1

В первой урне было 4 красных и 6 синих шара. Во второй урне 3
красных и 5 синих. Один шар переложили из первой во вторую
урну, и после этого из второй вытащили один шар. Какова
вероятность, что он синий?
Какова
вероятность?
10 шаров
Иванов О.В., Соколихин А.А. 2005
8 шаров
15

16. Задача 1

А достали синий шар из 2 й урны
Н1 переложили красный шар
Н 2 переложили синий шар
2
P ( H1 )
5
3
P( H 2 )
5
5
6
P ( A / H1 )
P( A / H 2 )
9
9
P ( A) P( H1 ) P( A / H1 ) P ( H 2 ) P ( A / H 2 )
2 5 3 6 28
P ( A)
5 9 5 9 45
Иванов О.В., Соколихин А.А. 2005
16

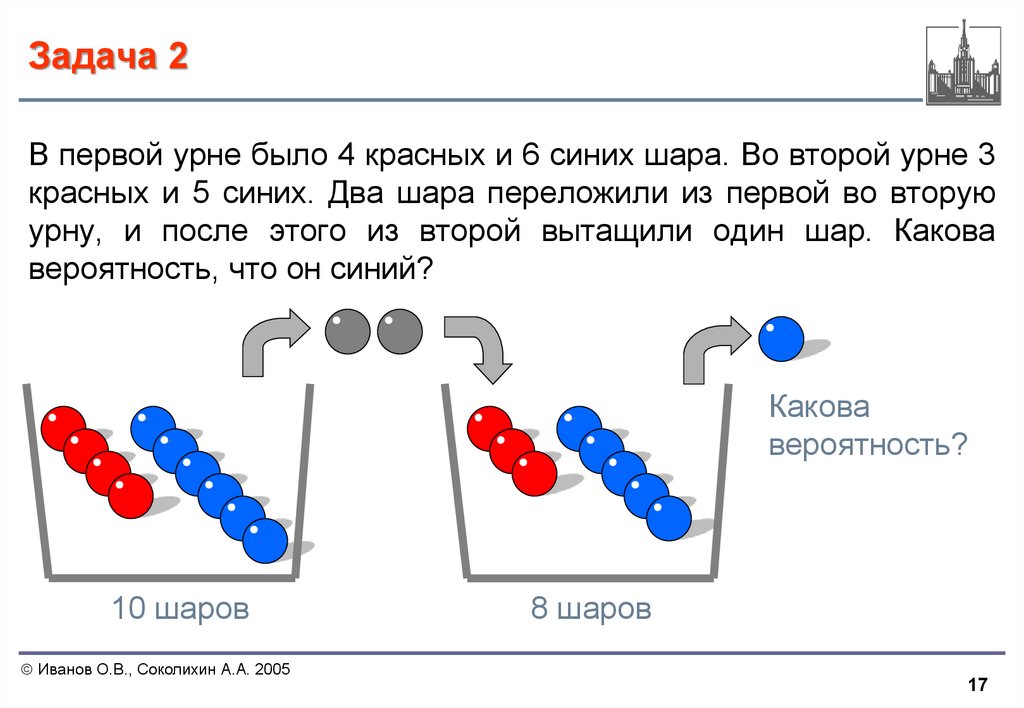
17. Задача 2

В первой урне было 4 красных и 6 синих шара. Во второй урне 3
красных и 5 синих. Два шара переложили из первой во вторую
урну, и после этого из второй вытащили один шар. Какова
вероятность, что он синий?
Какова
вероятность?
10 шаров
Иванов О.В., Соколихин А.А. 2005
8 шаров
17

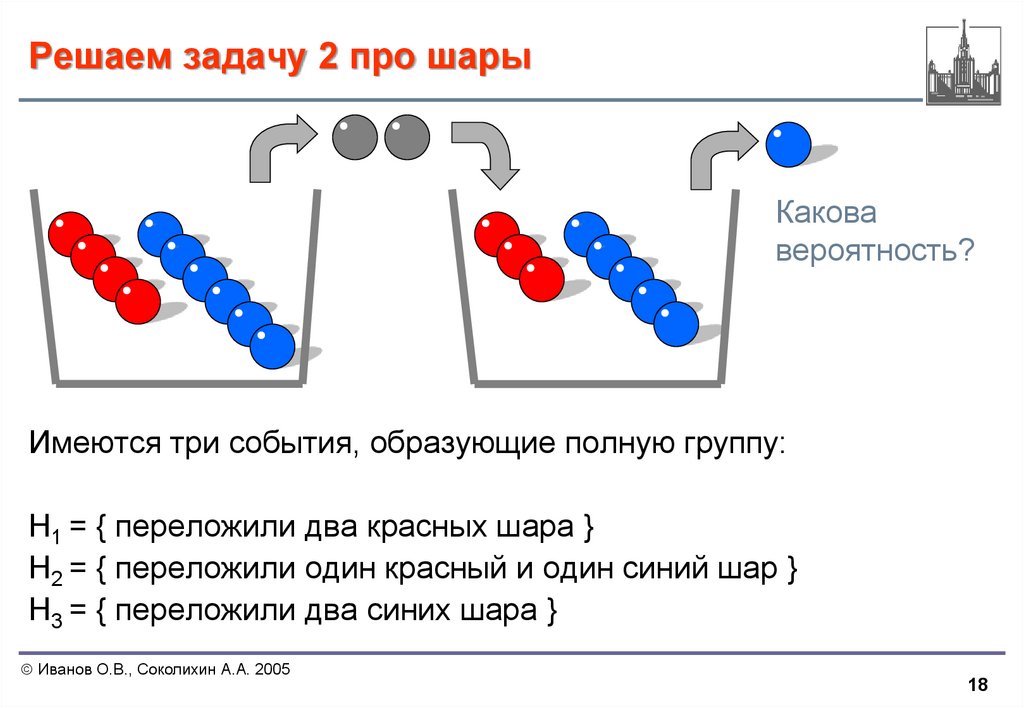
18. Решаем задачу 2 про шары

Какова
вероятность?
Имеются три события, образующие полную группу:
H1 = { переложили два красных шара }
H2 = { переложили один красный и один синий шар }
H3 = { переложили два синих шара }
Иванов О.В., Соколихин А.А. 2005
18

19. Решаем задачу 2 про шары

Какова
вероятность?
Находим вероятности этих событий:
P(H1) = 4/10 ∙ 3/9
P(H2) = 4/10 ∙ 6/9 + 6/10 ∙ 4/9
P(H3) = 6/10 ∙ 5/9
Иванов О.В., Соколихин А.А. 2005
= 2/15
= 8/15
= 5/15
19

20. Решаем задачу 2 про шары

Находим условные вероятности:
P(A/H1) = 5/10
P(A/H2) = 6/10
P(A/H3) = 7/10
Подставляем в формулу полной вероятности:
P(A)
= P(H1)∙P(A/H1) + P(H2)∙P(A/H2) + P(H3)∙P(A/H3) =
= 2/15 ∙ 5/10
+ 8/15 ∙ 6/10
+ 5/15 ∙ 7/10
=
= 31/50 = 0,62
Иванов О.В., Соколихин А.А. 2005
20

21. Задача 3

Из пяти винтовок, среди которых 3 снайперские и 2 обычные, наудачу
выбирается одна, и из нее производится выстрел. Найти вероятность
попадания, если вероятность попадания из снайперской винтовки-0,99, а из
обычной 0,7.
Иванов О.В., Соколихин А.А. 2005
21

22. Задача 4

На первом заводе выпускают 60% батареек данной фирмы, а остальные
выпускают на втором заводе. Вероятность брака на первом заводе
составляет 3%, на втором 20%. Найдите вероятность того, что взятая
наугад батарейка окажется бракованной.
Иванов О.В., Соколихин А.А. 2005
22

23. Задача 5

Ковбой Джон ненавидит мух. Мухобойка – не предмет джентльменов. Джон
просто стреляет в неё из попавшего под руку револьвера. Он попадает в муху на
стене с вероятностью 0,8, если стреляет из своего револьвера. Если Джон стреляет
из какого-нибудь револьвера, то он попадает в муху с вероятностью 0,2. На столе
лежат 10 револьверов, среди них два его. Ковбой Джон видит на стене муху, по
привычке наудачу хватает первый попавшийся револьвер и стреляет. Найдите
вероятность того, что муха погибла.
Иванов О.В., Соколихин А.А. 2005
23

24. Задача 6

Две фабрики выпускают одинаковые лобовые автомобильные стекла.
Первая фабрика выпускает 55% этих стекол, вторая — 45% . Первая
фабрика выпускает 5% бракованных стекол, а вторая — 3% . Найдите
вероятность того, что случайно купленное в магазине стекло окажется
бракованным.
Иванов О.В., Соколихин А.А. 2005
24