Похожие презентации:
Системы уравнений с двумя переменными (9 класс)
1. Системы уравнений с двумя переменными
Алгебра – 9 класс2.
Закончите определение:Пару значений (х;у), которая одно –
временно является решением и
первого и второго уравнений,
называют …
решением системы уравнений.
3.
Какая из следующих пар чисел является решениемсистемы уравнений:
x y 1
y 2x 1
2
а). (0;1)
б). (-1;-1)
2
в). (1;0)
г). (1;1)
б).
неявляется
является
решением
системы
уравнений
а).
(0;1)
решением
системы
уравнений
в).
г). (-1;-1)
(1;0)
(1;1)–––является
не
решением
системы
уравнений
т.к.
т.к.
т.к. 2 22 2 2
2
2
2
0
1
1
( 11) 1 0(
1)1 1 неверно
верно
верно
неверно
неверно
неверно
110 222 1 ( 0 1 1
1) 11 1 верно
4.
Закончите определение:Решить систему уравнений – это
значит …
найти все её решения или
установить, что решений нет.
5.
Алгоритм графического метода прирешении системы двух уравнений с двумя
переменными х, у.
1. Построить график первого уравнения.
2. Построить график второго уравнения.
3. Найти точки пересечения графиков.
4. Координаты каждой точки пересечения
являются решениями системы уравнений.
6.
Какая функция называетсялинейной функцией?
Функция вида y kx m , где k , m - числа, а
х, y - переменные, называется линейной функцией.
Что является графиком
линейной функции?
Графиком линейной функции является прямая.
7.
k<0k>0
8.
Какая функция называетсяквадратичной функцией?
Функция вида y ax bx c , где a, b, c - числа,
причём a 0 , а х, y - переменные, называется
квадратичной функцией.
2
Что является графиком
квадратичной функции?
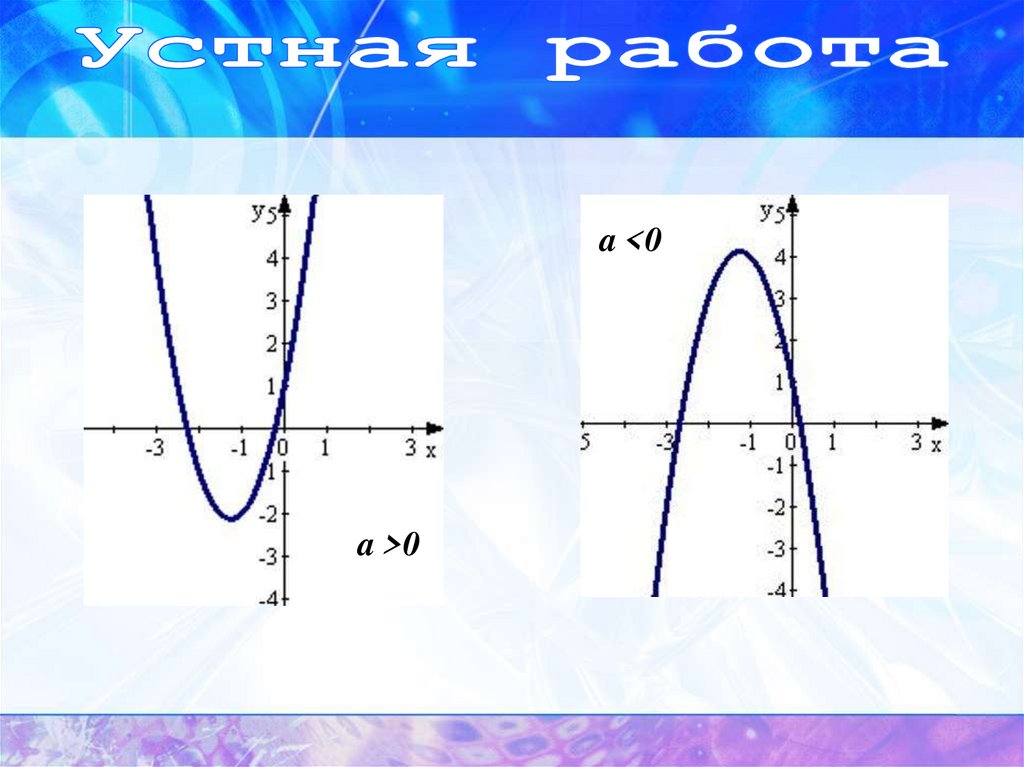
Графиком квадратичной функции является парабола.
9.
a <0a >0
10.
Какая функция называетсяобратной пропорциональностью?
k
Функция вида y
, где k 0 - число, а
x
х, y - переменные, называется
функцией обратной пропорциональностью.
Что является графиком
обратной пропорциональности?
Графиком обратной пропорциональности является
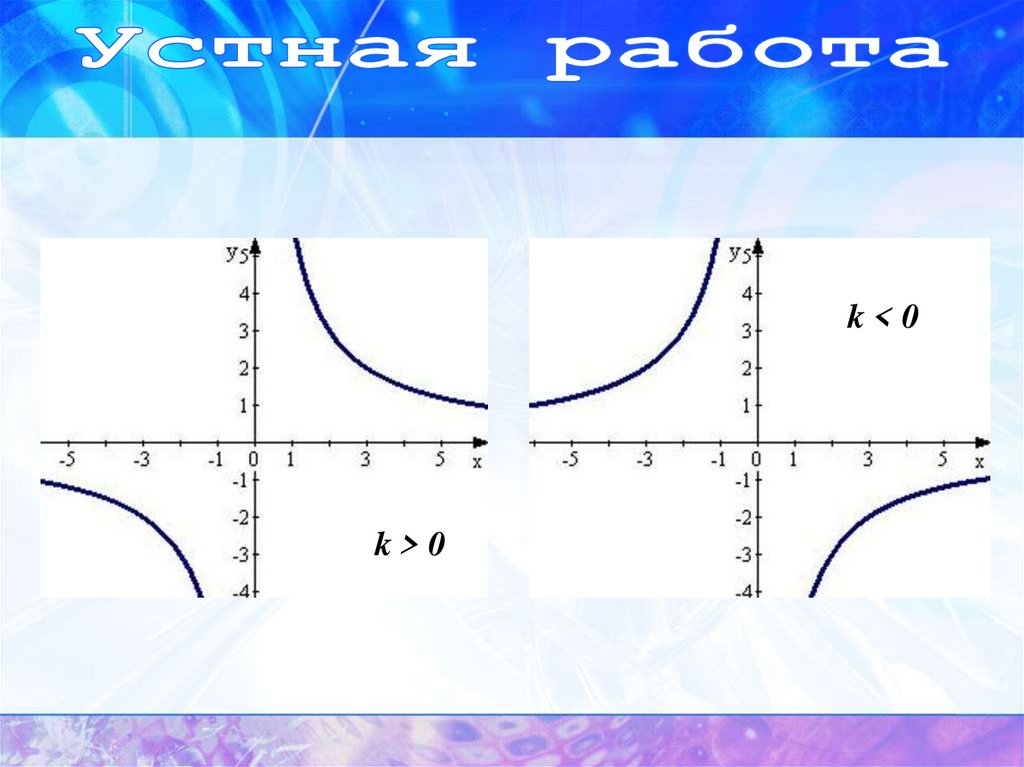
гипербола.
11.
k<0k>0
12.
Какая фигура является графикомуравнения
x a y b R ?
2
2
2
Графиком уравнения является окружность с центром
в точке (a;b) и радиусом R.
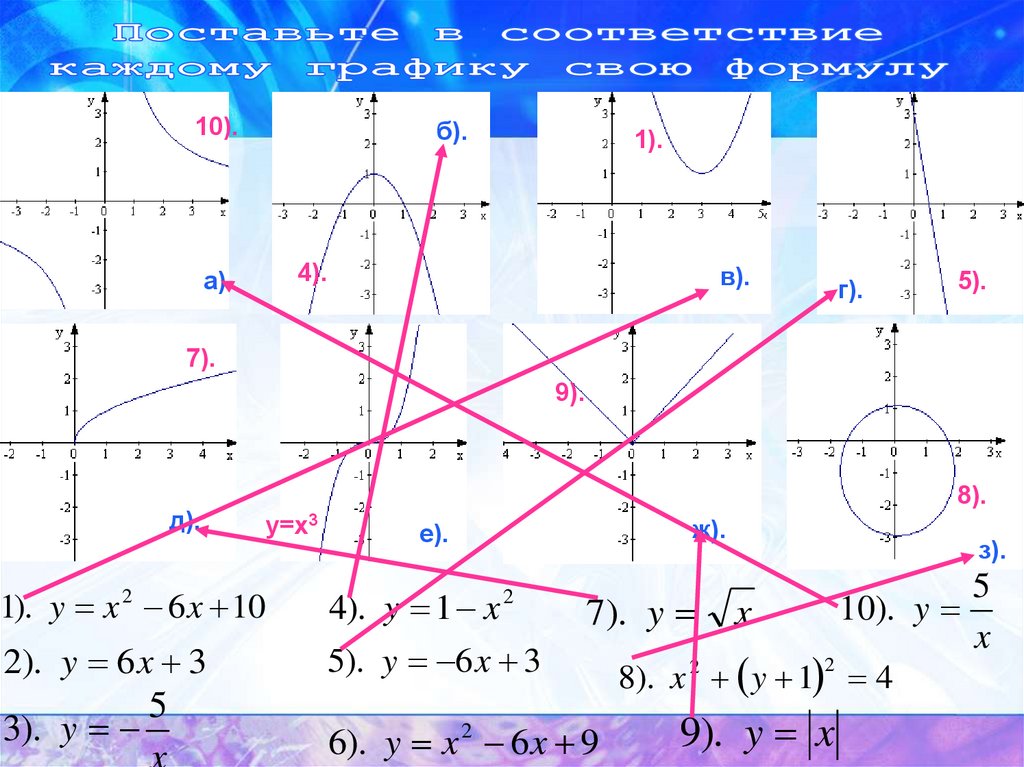
13.
б).10).
1).
в).
4).
а).
г).
5).
7).
9).
д).
8).
y=x3
1). y x 6 x 10
2
2). y 6 x 3
5
3). y
ж).
е).
4). y 1 x
5). y 6 x 3
2
7). y
6). y x 2 6 x 9
з).
5
10). y
x
x
8). x 2 y 1 4
2
9). y x
14.
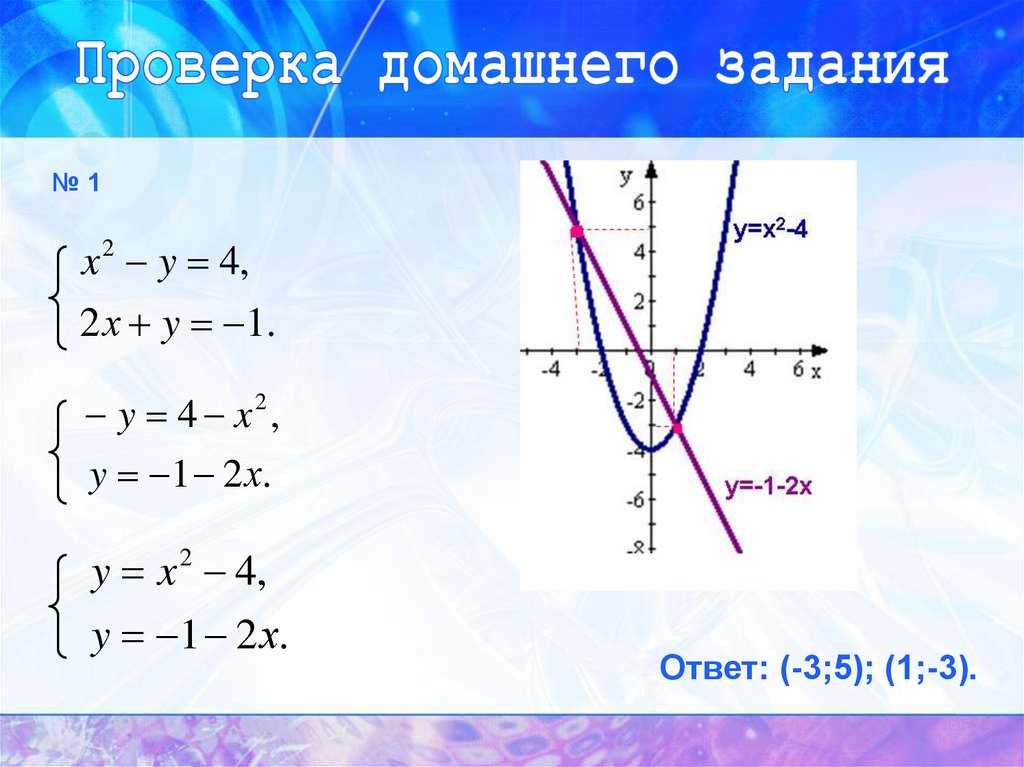
№1x 2 y 4,
2 х y 1.
y 4 x ,
y 1 2 х.
2
y x 2 4,
y 1 2 х.
Ответ: (-3;5); (1;-3).
15.
№28
y ,
x
x 2 y.
8
y ,
x
y 2 x.
Ответ: (-2;4); (4;-2).
16.
Решить систему уравненийметодом подстановки
у х 5,
х 5 2 2 х х 5 х 2 7
у 2 2 ху х 2 7.
х 2 10 х 25 2 х 2 10 х х 2 7 0
2 х 2 20 х 32 0
у х 5,
х 5 2 2 х х 5 х 2 7
х 2,
у 2 5
х 2,
у 3.
или
х 8,
у 8 5
или
х 8,
у 3.
х 2 10 х 16 0
х1 2; х 2 8
Ответ: (-2;3); (-8;-3)
17.
1). Графический метод2). Метод подстановки
3). Метод алгебраического
сложения
4). Метод введения новой
переменной
18.
Алгоритм метода подстановкипри решении системы двух уравнений с двумя переменными х, у.
1).
Выразить у через х.
2).
Подставить полученное выражение вместо у в другое
уравнение системы.
3).
Решить полученное уравнение относительно х.
4).
Подставить поочерёдно каждый из найденных на
третьем шаге корней уравнения вместо х в выражение,
полученное на первом шаге.
5).
Записать ответ в виде пар значений (х;у), которые
были найдены соответственно на третьем и четвёртом
шаге.
19. Решить систему уравнений методом алгебраического сложения
20. Решите систему уравнений методом введения новой переменной .
21. Выполните тестовые задания
22. Коды правильных ответов
Тест 2.1.ББВАГА
Тест 2.2.
ВГГВГБ


















 Математика
Математика








