Понятие системы уравнений с двумя переменными

1.

2. I.Понятие системы уравнений с двумя переменными.

ОПРЕДЕЛЕНИЕ. Если нужно найти пару чисел (x;y), таких что
они одновременно удовлетворяют рациональным уравнениям: p(x;y)=0 и
u(x;y)=0, то принято говорить, что они образуют систему уравнений:
Решение системы – это пара чисел (х; у), которая одновременно
является решением и первого и второго уравнений системы.
Решить систему – это значит найти все ее решения или установить,
что решений нет.

3.

Решение обычно записывают в круглых скобках: например,
(2;5).
Переменные в системе можно обозначать любыми буквами, чаще всего
обозначают латинскими буквами, но стоит помнить, что первой
записывают переменную, которая встречается раньше в алфавите.
Для решения систем уравнений используют различные методы:
графический метод,
метод подстановки,
метод сложения,
метод замены переменой.

4. II. Графический метод решения системы уравнений с двумя переменными.

№1.
х 2 у 2 25
х 5 у 0
Решение:
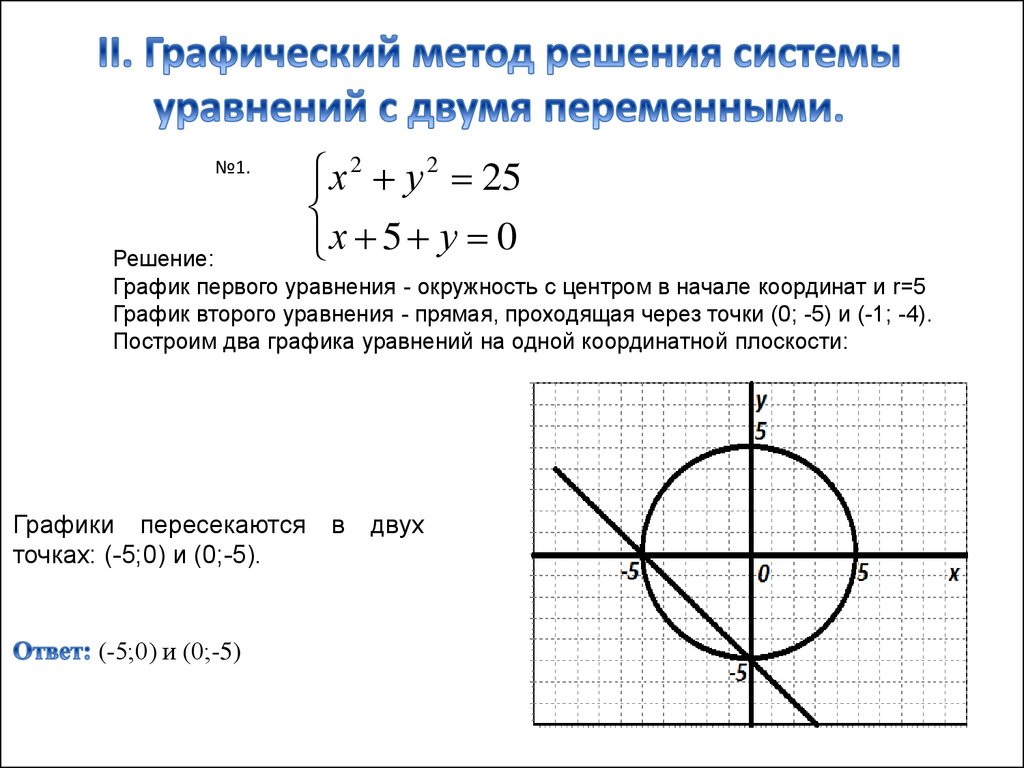
График первого уравнения - окружность с центром в начале координат и r=5
График второго уравнения - прямая, проходящая через точки (0; -5) и (-1; -4).
Построим два графика уравнений на одной координатной плоскости:
Графики пересекаются в
точках: (-5;0) и (0;-5).
(-5;0) и (0;-5)
двух

5.

№2
Решить систему уравнений:
Решение.
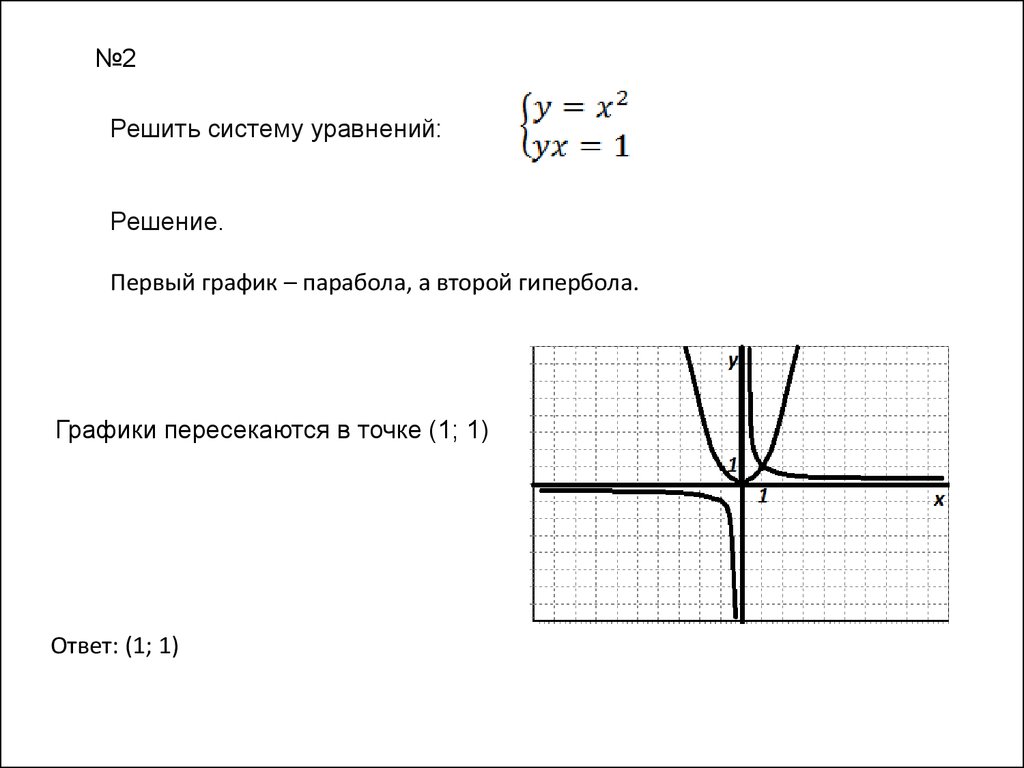
Первый график – парабола, а второй гипербола.
Графики пересекаются в точке (1; 1)
Ответ: (1; 1)