Комплексные числа и координатная плоскость

1.

Учитель:
Печенкина
Евгения
Евгеньевна

2.

Домашнее
задание:
§33
№ 33.1
№33.4

3.

Математический
диктант
Задание №1:

4.

Задание №2:

5.

6.

Задание №7:

7.

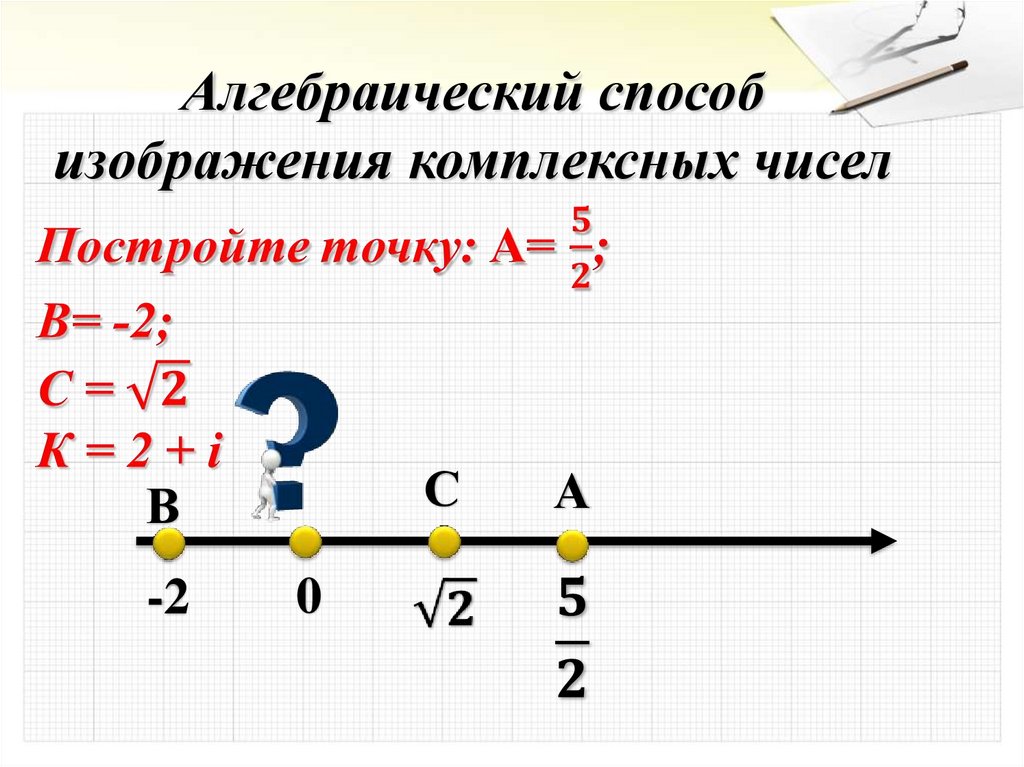
Алгебраический способ
изображения комплексных чисел
С
В
-2
0
А

8.

Комплексные числа
и
координатная
плоскость

9.

Способы
изображения
комплексных чисел
Алгебраический
способ
Векторный
способ

10.

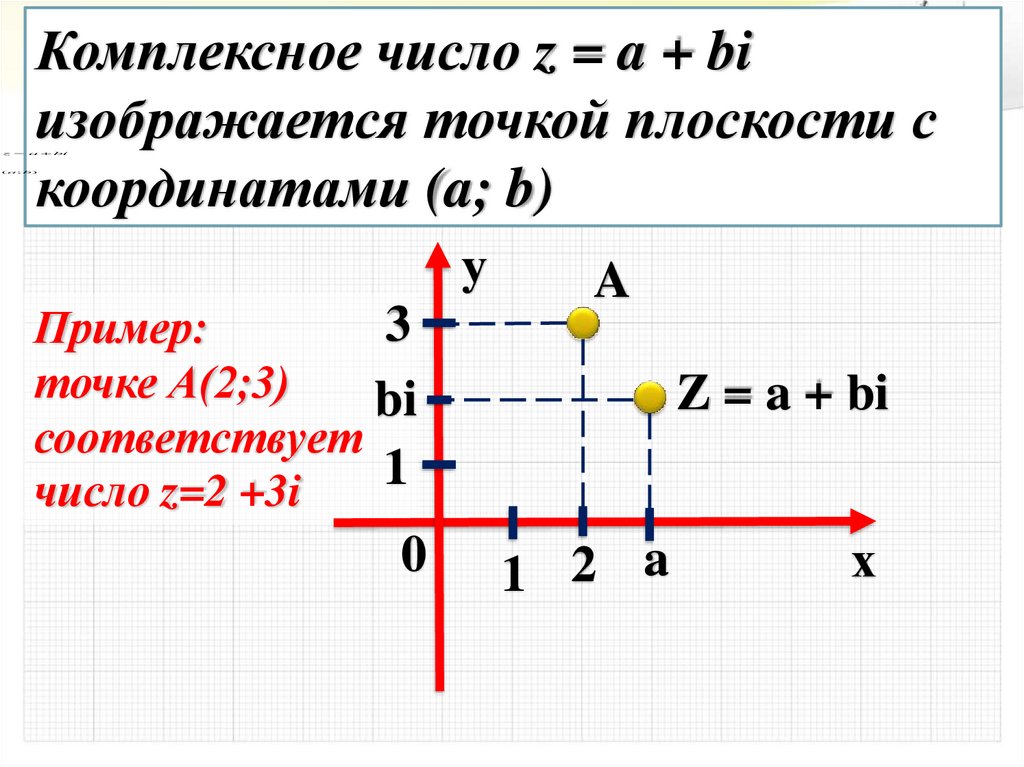
z
Комплексное число z = a + bi
изображается точкой плоскости с
координатами (a; b)
a bi
( a; b )
у
3
Пример:
точке А(2;3)
bi
соответствует
1
число z=2 +3i
0
A
Z = a + bi
1 2 a
х

11.

Вопрос: Возможно, что одной и той же
точке плоскости, например, точке А(а,b)
будут соответствовать различные
комплексные числа?
;
Таким образом, множество всех
комплексных чисел находится во
взаимно однозначном соответствии с
множеством всех точек плоскости.

12.

Действительные числа а,
т.е. комплексные числа вида
а + 0i, изображаются точками
с координатами (а;0), т.е.
точками оси абсцисс.
Im
1
0
Чисто мнимые числа bi=0 + bi
изображаются точками с
координатами (0;b), т.е.
точками оси ординат
1
Re

13.

Точка с координатами (0;b)
обозначается bi.
Im
i
Например:
Точка (0;1) обозначается i,
точка (0;-1) – это точка – i,
точка (0;2) – это точка 2i.
Начало координат - это точка О
-i
0 1
Re

14.

Плоскость, на которой
изображаются комплексные
числа, называется
комплексной плоскостью.

15.

Пример: Изобразите на координатной
плоскости множество всех
комплексных чисел, у которых:
а) действительная часть равна -4;
б) мнимая часть является четным
однозначным натуральным числом.

16.

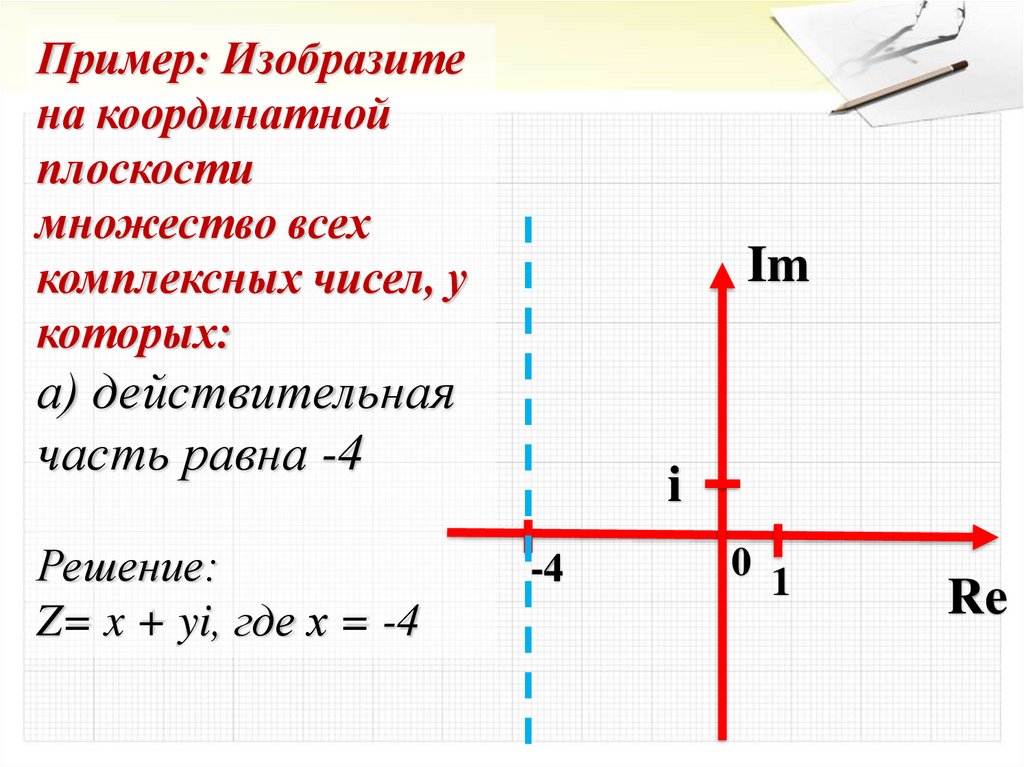
Пример: Изобразите
на координатной
плоскости
множество всех
комплексных чисел, у
которых:
Im
а) действительная
часть равна -4
Решение:
Z= x + yi, где х = -4
i
-4
0 1
Re

17.

Пример:
Изобразите на
координатной плоскости
множество всех
комплексных чисел, у
которых:
б) мнимая часть является
четным однозначным
натуральным числом
Решение:
z= x + yi , у которых
у = 2,4,6,8
Im
8i
6i
4i
2i
i
Re
0 1

18.

Вопрос: В чем же состоит
алгебраический способ
изображения комплексных чисел?
(Любую точку на координатной
плоскости можно воспринимать
как упорядоченную пару (а;b)
действительных чисел)

19.

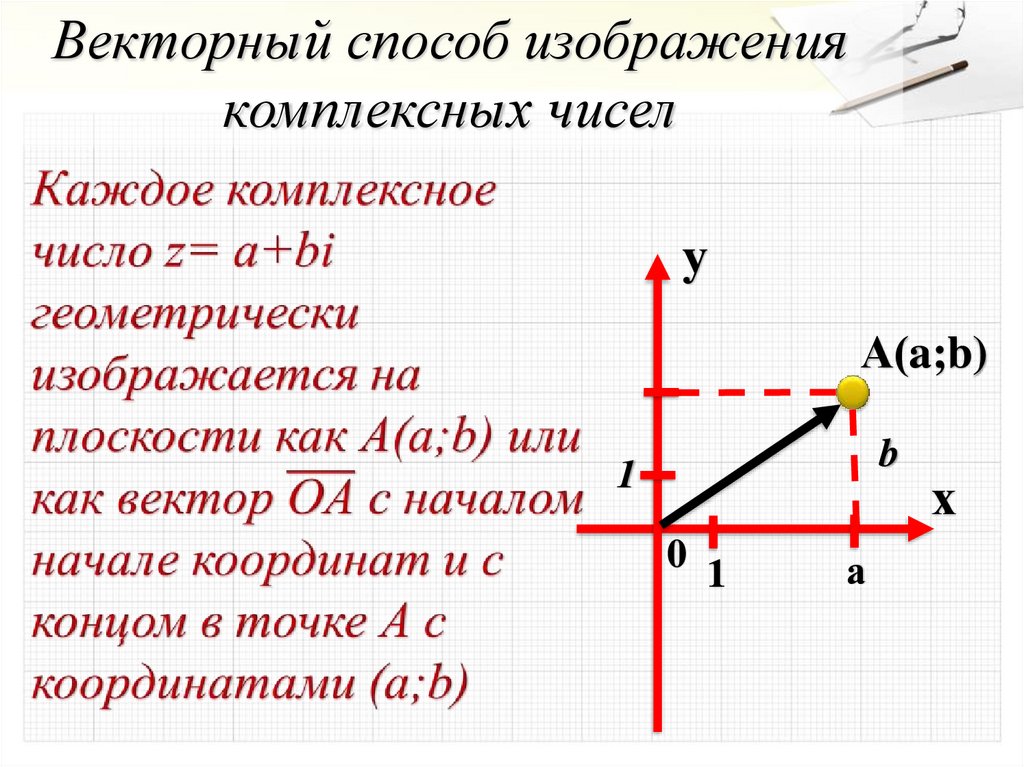
Векторный способ изображения
комплексных чисел
у
А(a;b)
b
1
0 1
а
х

20.

Действия над
комплексными числами
Геометрическое
изображение
суммы
комплексных чисел
Геометрическое
изображение
разности
комплексных чисел
Геометрическое
изображение
сопряженных
комплексных чисел

21.

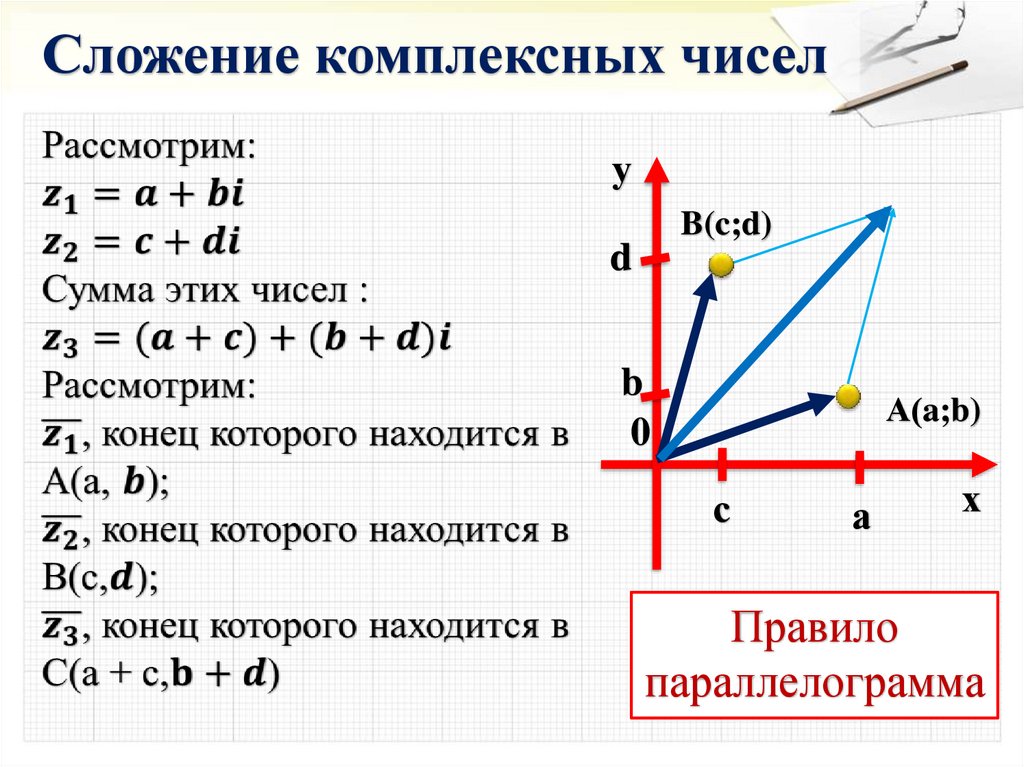
Сложение комплексных чисел
у
B(c;d)
d
b
0
А(a;b)
с
а
х
Правило
параллелограмма

22.

23.

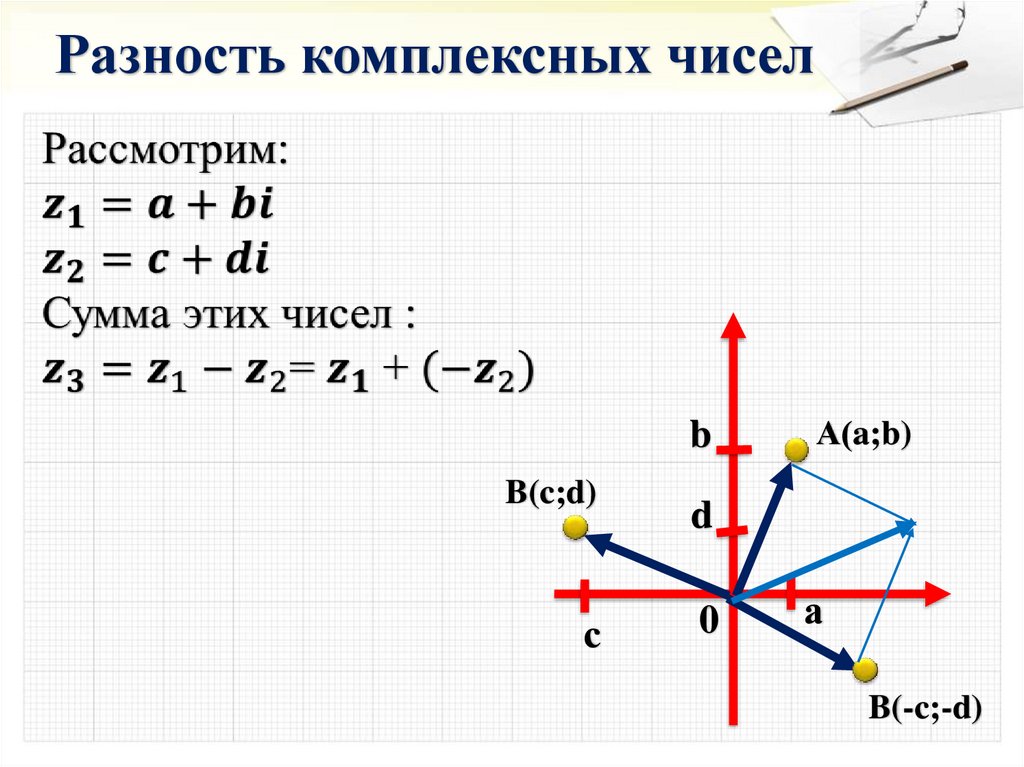
Разность комплексных чисел
b
B(c;d)
с
А(a;b)
d
0
а
B(-c;-d)

24.

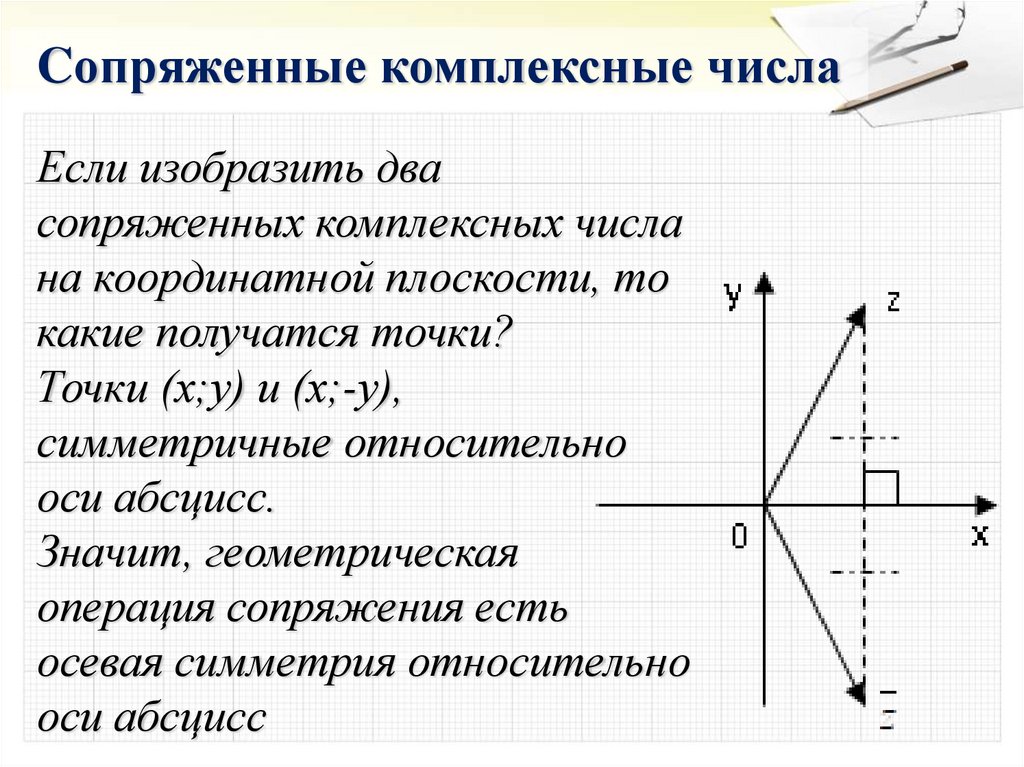
Cопряженные комплексные числа
Если изобразить два
сопряженных комплексных числа
на координатной плоскости, то
какие получатся точки?
Точки (х;у) и (х;-у),
симметричные относительно
оси абсцисс.
Значит, геометрическая
операция сопряжения есть
осевая симметрия относительно
оси абсцисс

25.

26.

б) Соедините заданные точки
последовательно отрезками.
Сколько получилось точек
пересечения с осями координат?
Запишите комплексные числа,
которым соответствуют эти
точки.

27.

Задания из
учебника:
№33.6
№33.15

28.

Самостоятельная
работа