Комплексные числа. Модуль и аргумент комплексного числа

1.

Комплексные
числа

2.

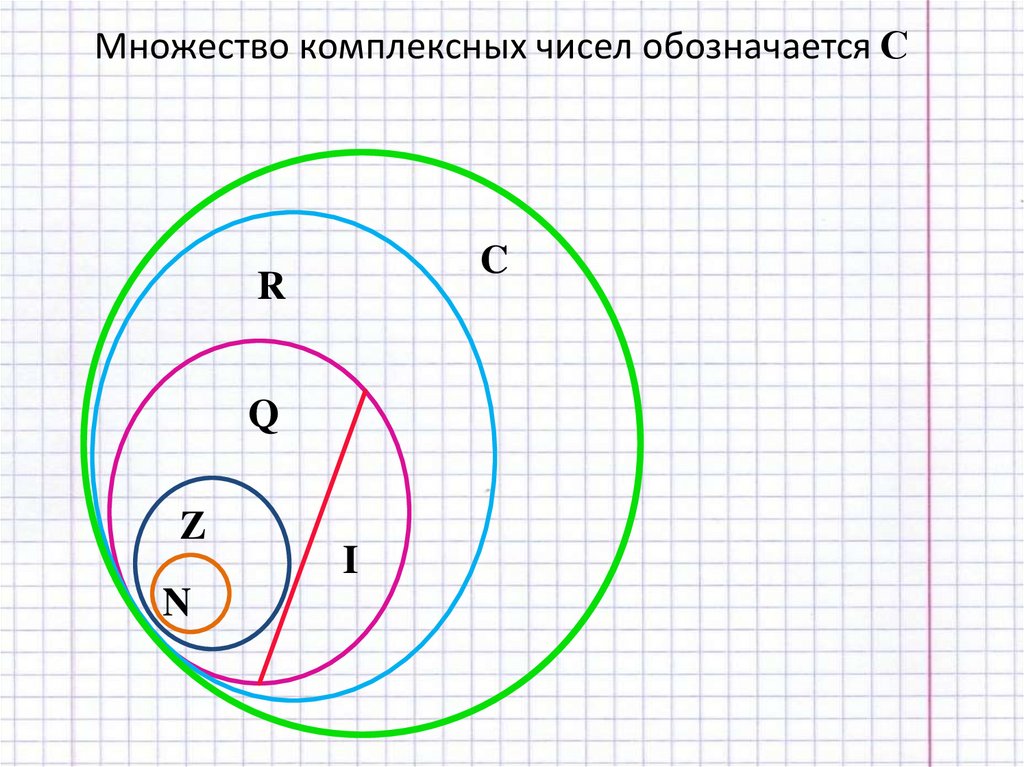
Множество комплексных чисел обозначается С
C
R
Q
Z
N
I

3.

Термин “мнимые числа” ввел в 1637 году
французский математик и философ Р. Декарт,
а в 1777 году один из крупнейших
математиков XVIII века - Л. Эйлер предложил
использовать первую букву французского
слова imaginaire (мнимый) для обозначения
числа i(мнимой единицы). Этот символ
вошел во всеобщее употребление благодаря
К. Гауссу . Термин “комплексные числа” так
же был введен Гауссом в 1831 году. Слово
«комплекс» (от латинского complexus)
означает связь, сочетание, совокупность
понятий, предметов, явлений и т. д.
образующих единое целое.

4.

Большой вклад в развитие теории функций комплексного
переменного внесли русские и советские ученые:
Н. И. Мусхелишвили занимался ее
применениями к теории упругости;
М. В. Келдыш и
М. А. Лаврентьев - к
аэро- и гидродинамике;
Н. Н. Богомолов и В. С. Владимиров
- к проблемам квантовой теории
поля.

5.

ОпределениеКомплексным
:
числом
называется число вида a+bi ,
где a, b − некоторые
действительные числа, а i−
мнимая единица, причем:
i 1, i 1 .
2
Обозначение:
z a b i
алгебраическая форма записи
комплексного числа

6.

z a b i
a - действительная часть
b -мнимая часть
комплексного числа z.
Обозначается a=Re z.
комплексного числа z.
Обозначается b=Im z.

7.

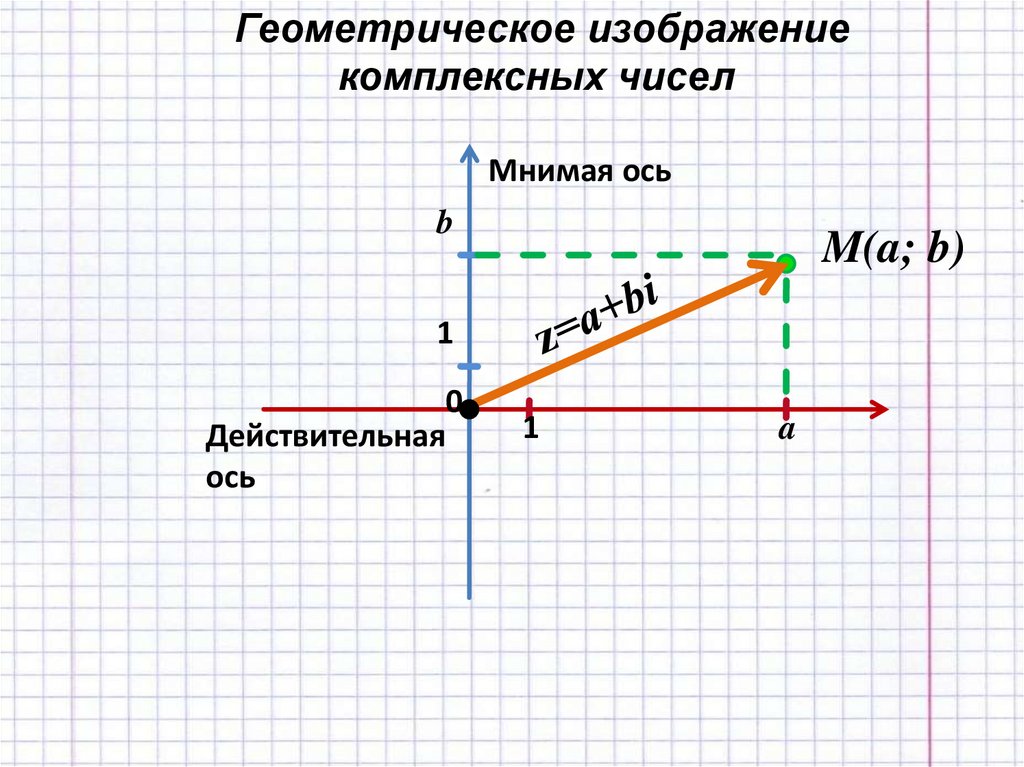
Геометрическое изображение
комплексных чисел
Мнимая ось
b
M(a; b)
1
0
Действительная
ось
1
a

8.

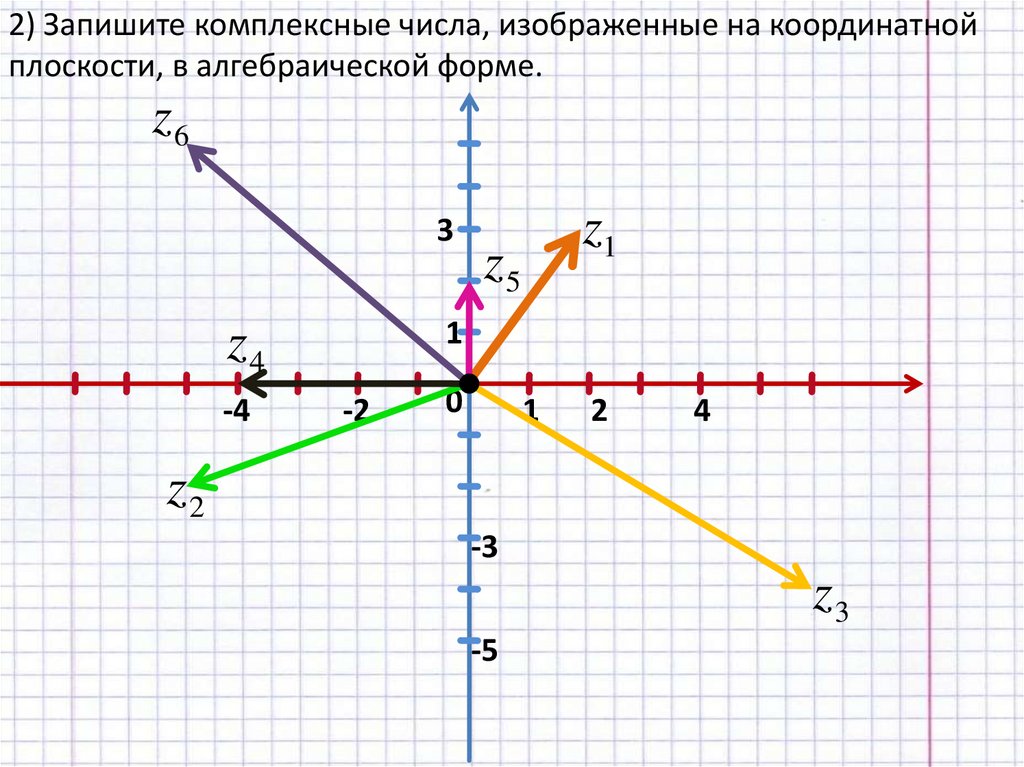
2) Запишите комплексные числа, изображенные на координатной
плоскости, в алгебраической форме.
z6
3
z5
1
z4
-4
z1
-2
0
1
2
4
z2
-3
z3
-5

9.

Примеры:
1) Изобразите комплексные числа на плоскости
z1 1 5i;
z 2 7 3i;
z3 1,5 5i;
z 4 3,5 2i
z5 3
z6 6i
z 7 2 i;

10.

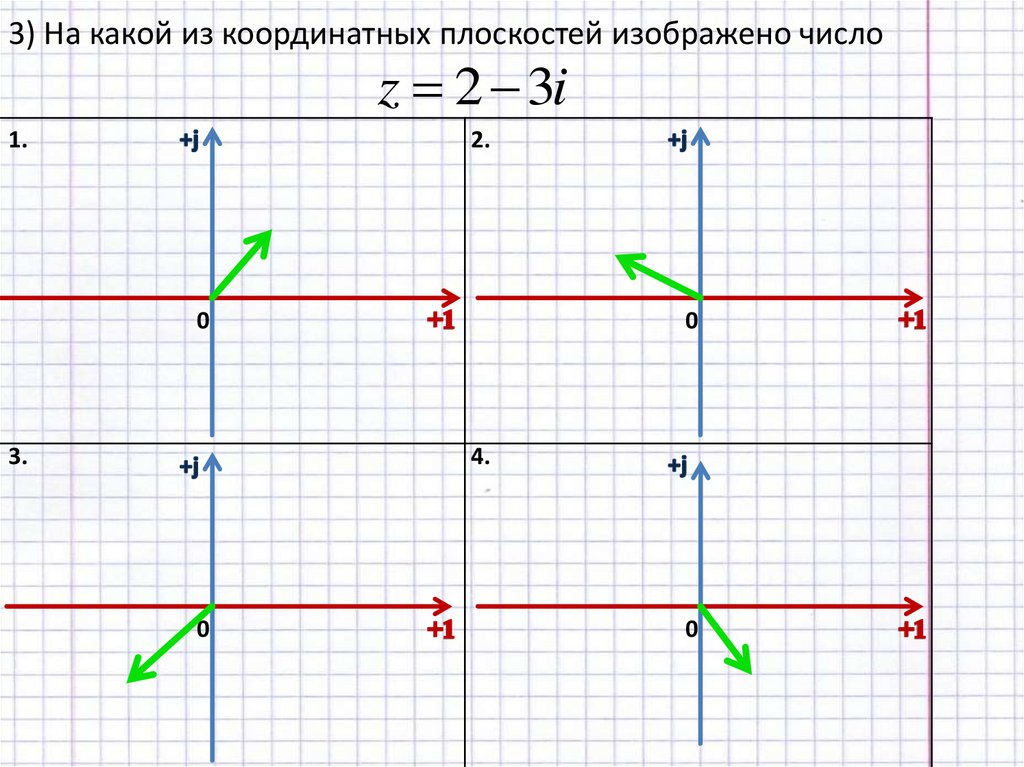
3) На какой из координатных плоскостей изображено число
z 2 3i
1.
2.
0
3.
0
4.
0
0

11.

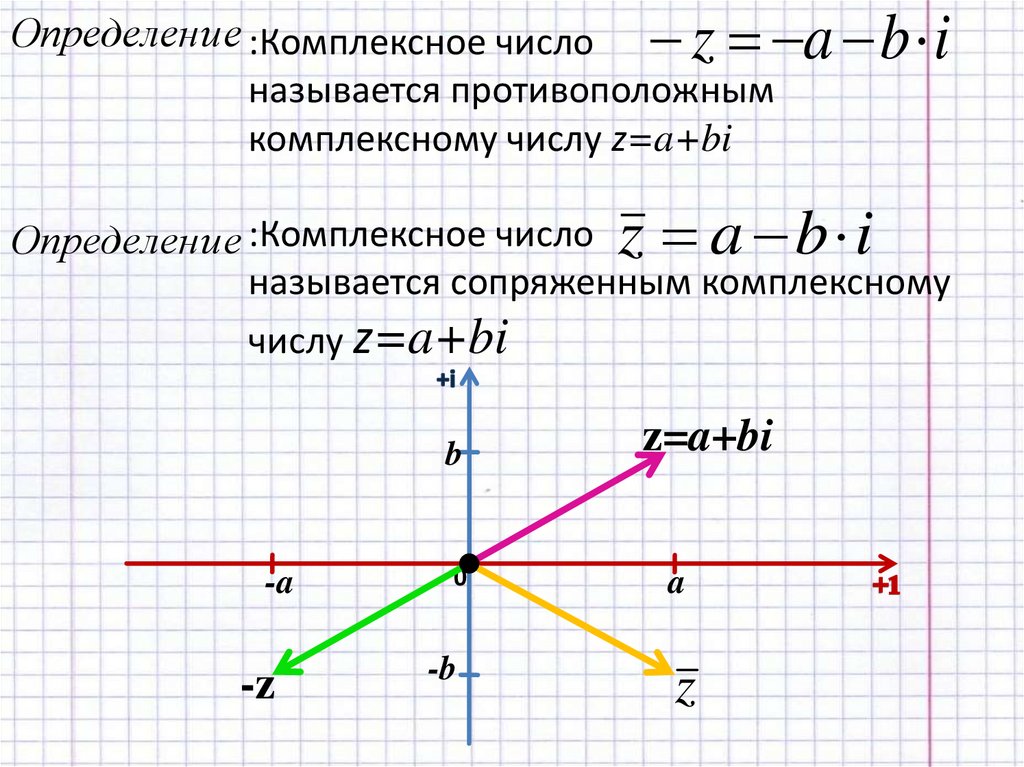
Определени е :Комплексное число z a b i
называется противоположным
комплексному числу z=a+bi
Определени е :Комплексное число z a b i
называется сопряженным комплексному
числу z=a+bi
b
-a
-z
0
-b
z=a+bi
a
z

12.

Примеры:
1. Запишите числа, противоположные и сопряженные
данным:
z1 7 3i
z 2 1 5i
z3 i 1
z 4 5i
z5 6
2. Какие из данных чисел являются сопряженным и
противоположным для числа
z 3 2i
а) z 3 2i
б ) z 3 2i
в) z 3 2i
г ) z 3i 2.

13.

Модуль и аргумент
комплексного
числа

14.

Определени е: Модулем комплексного числа z a b i
называется действительное число
r z a b 0.
2
Примеры:
Найти модуль комплексных чисел:
z1 3 4i r1 z1
z 2 12 5i
z3 1 3i
z 4 3
z5 2i
2

15.

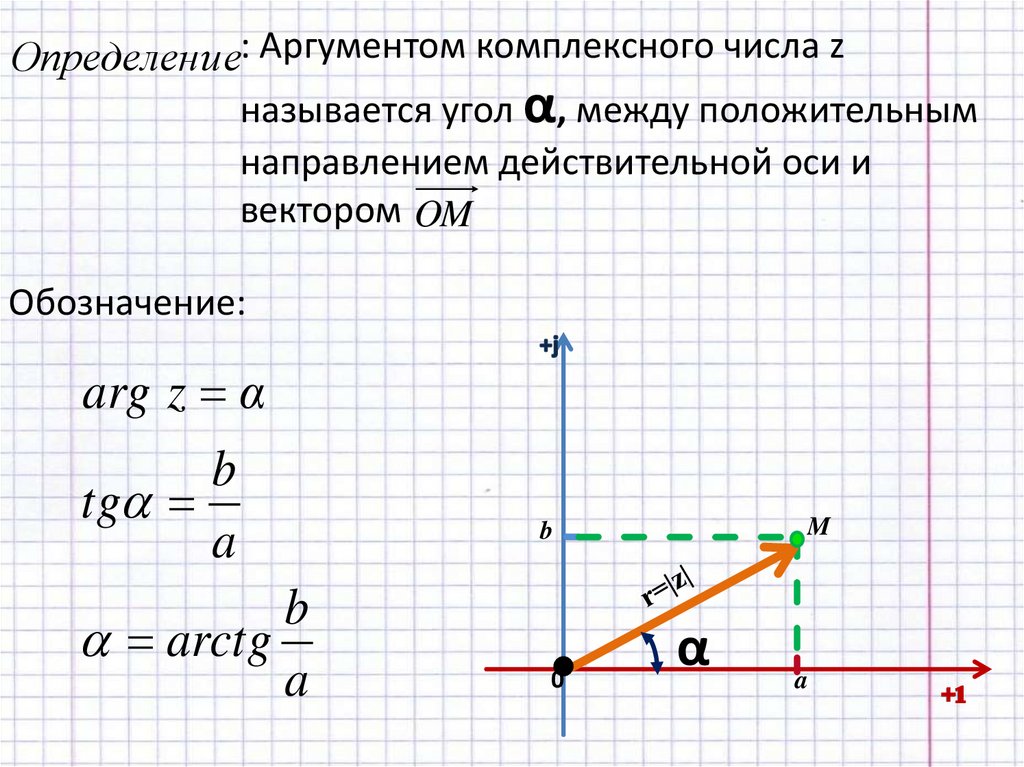
Определени е: Аргументом комплексного числа z
называется угол α, между положительным
направлением действительной оси и
вектором OM
Обозначение:
arg z α
b
tg
a
b
arctg
a
M
b
0
α
a

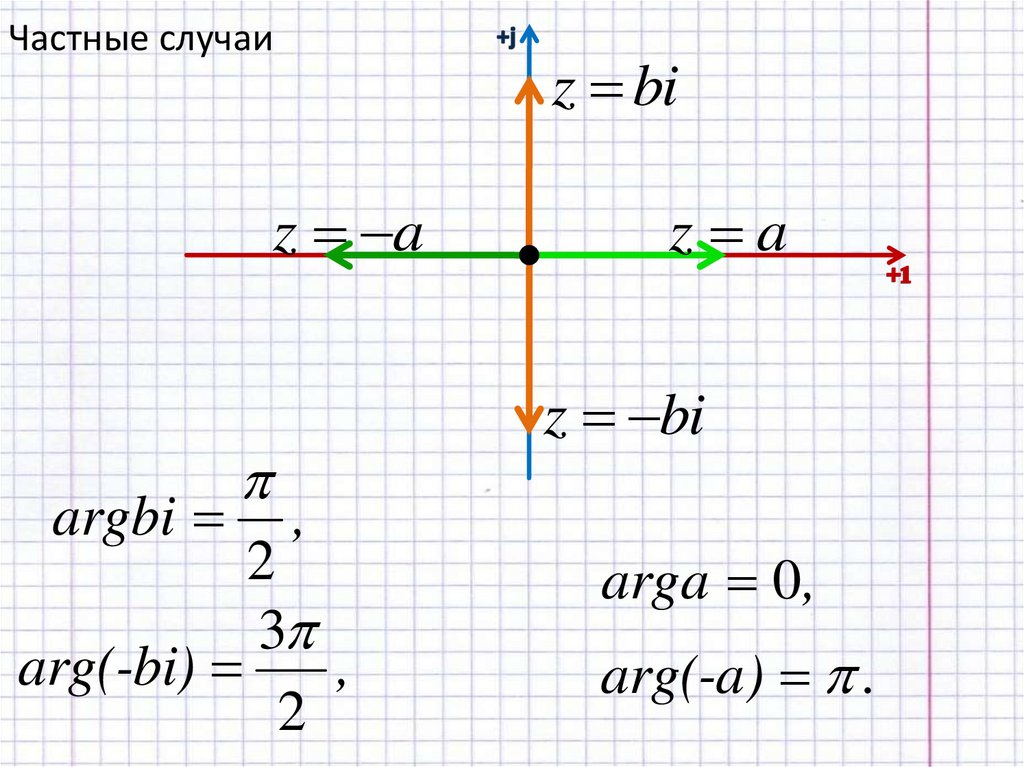
16.

Частные случаи
z bi
z a
argbi
z a
z bi
,
2
3
arg(-bi)
,
2
arga 0 ,
arg(-a) .

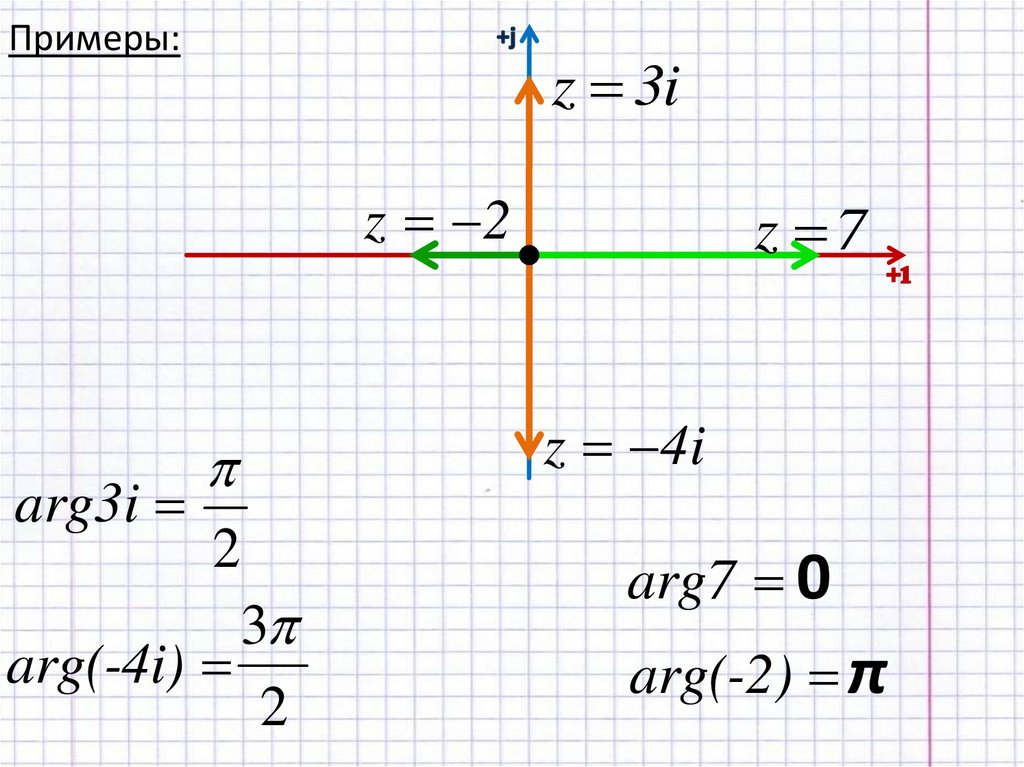
17.

Примеры:
z 3i
z 2
arg3i
2
3
arg(-4i)
2
z 7
z 4i
arg7 0
arg(-2) π