Похожие презентации:
Аппроксимация функций
1. § 4 Аппроксимация функций
4.1. Общая задача аппроксимацииАппроксимацией функции называется
приближённое представление сложной или
заданной в виде таблицы функции более простой
функцией, имеющей минимальные отклонения
от исходной функции.
2.
4.2. Интерполяция многочленамиx
x0
x1
...
xn
f(x)
y0
y1
...
yn
(x)
( x0 ) y0 ; ( x1) y1; ...; ( xn ) yn
f ( x) ?
x x0 ; xn интерполяция
x x0 ; xn экстраполяция
x0 ; x1; x2 ; .... xn узлы интерполяции
3.
Если приближение строится на заданном дискретноммножестве точек {xi}, то аппроксимация называется
точечной.
При построении приближения на непрерывном множестве
точек (например, на отрезке [a, b]) аппроксимация
называется непрерывной (или интегральной).
Интерполяция на всем участке [a, b] называется
глобальной, а на отдельных участках отрезка [a, b] –
кусочной или локальной.
4.
nn 1
Pn ( x) a0 x a1x
... an
интерполяционный многочлен
Pn ( x0 ) y0 ; Pn ( x1) y1; ...; Pn ( xn ) yn
Теорема. Какие бы ни были заданы значения функции в
n+1 узлах, всегда существует и притом единственный
многочлен степени не выше n, принимающий в этих узлах
заданные значения
5.
a x n a x n 1 a x n 2 ... a y1 0
2 0
n
0
0 0
a0 x1n a1x1n 1 a2 x1n 2 ... an y1
............................................................
n
n 1
n 2
a0 xn a1xn a2 xn ... an yn
x0n x0n 1 x0n 2 .... 1
x1n x1n 1 x1n 2 .... 1
............................. i j
xnn xnn 1 xnn 2 .... 1
xi x j 0
6.
4.3. Погрешность интерполированияПогрешность аппроксимации функции f (x) полиномом
ϕ(x ) можно оценивать по величине среднеквадратичного
отклонения Sa
или по значению максимального отклонения
7.
4.4. Интерполяционный многочлен Лагранжаx
x0
x1
...
xn
f(x)
y0
y1
...
yn
Ln (x)
Ln ( x0 ) y0 ; Ln ( x1) y1; ...; Ln ( xn ) yn
Ln ( x) l 0 ( x) l1 ( x) ... l n ( x)
8.
Ln ( x) l 0 ( x) l1 ( x) ... l n ( x)yi , если i k ;
li ( xk )
0, если i k.
li ( x) ci ( x x0 )( x x1)...(x xi 1)( x xi 1)...(x xn )
ci
yi
( x i x 0 )( x i x1 )...( x i xi 1 )( x i x i 1 )...( x i x n )
.
9.
li yi( x x0 )( x x1 )...( x xi 1 )( x xi 1 )...( x xn )
( xi x0 )( xi x1 )...( xi xi 1)( xi xi 1)...( xi xn )
n
( x x0 )( x x1)...( x xi 1)( x xi 1)...( x xn )
i 0
( xi x0 )( xi x1)...( xi xi 1)( xi xi 1 )...( xi xn )
Ln yi
10.
Пример. Построить интерполяционный многочлен Лагранжадля функции заданной таблицей.
x
–1
2
3
f(x)
12
3
4
11.
Пример. Построить интерполяционный многочлен Лагранжадля функции заданной таблицей.
n
Ln yi
i 0
x
–1
2
3
f(x)
12
3
4
( x x 0 )( x x1 )...( x xi 1 )( x x i 1 )...( x x n )
( x i x 0 )( x i x1 )...( x i xi 1 )( xi x i 1 )...( x i x n )
L2 ( x) 12
( x 2)( x 3)
( 1 2)( 1 3)
3
( x 1)( x 3)
( 2 1)( 2 3)
4
( x 1)( x 2)
(3 1)( 3 2)
( x 2 5 x 6) ( x 2 2 x 3) ( x 2 x 2) x 2 4 x 7
.
12.
n 1 ( x) ( x x0 )( x x1 )...( x xn )n 1( x) ( x x0 )( x x1)...(x x j 1)( x x j 1)...(x xn )
n 1 ( xi ) ( xi x0 )( xi x1 )...( xi xi 1 )( xi xi 1 )...( x xn )
n
Ln ( x)
i 0
y i n 1 ( x)
( x xi ) n 1 ( xi )
13.
xx0
x1
x2
x3
x0
x–x0
x0 – x1 x0 – x2 x0 – x3
x1
x1–x0 x – x1 x1 – x2 x1 – x3
x2
x2 – x0 x2 – x1 x – x2 x2 – x3
x3
x3 – x0 x3 – x1 x3 – x2 x – x3
pi
yi
yi / pi
n y
i
S
pi ( x xi ) n 1 ( xi )
i 0 pi
n y
Ln ( x) n 1( x) i
i 0 pi
14.
Погрешность формулы Лагранжа15.
Многочлен Лагранжа для равноудаленных узловxi x0 ih, i 0,1,...n,
h 0 шаг интерполяции
x x0
q
h
yi f xi
xi x0 x0 ih x0
qi
i
h
h
x x j h q j
xi x j h i j
16.
L1( x) L1( x0 hq ) 1 q y0 qy1q j
Ln ( x) Ln ( x0 hq)
yi
i 0 j i i j
n
n
n i q q 1 ... q i 1 q i 1 ... q n
1
i 0
i! n j !
yi
17.
hn 1 M n 1
max f ( x) Ln ( x) h
n
n 1 !
x0 ; xn
n max q q 1 .... q n
0; n
h
n 1
M n 1 max f
( x)
x0 ; xn
18.
4.5. Интерполяционные многочлены НьютонаКонечной разностью первого порядка называется
разность между двумя соседними значениями
функции f:
yi yi 1 yi
i 0,1, ..., n 1
Конечной разностью порядка р называется разность
двух последовательных разностей порядка р-1:
p yi p 1 yi 1 p 1 yi
i 0,1,..., n 1
19.
Таблица конечных разностейxi
yi
x0
y0
x1
y1
x2
y2
x3
y3
….
….
yi
2
yi
3 yi
y0
2
3
k yi h k f k
xi ; xi kh
y0 y0
y1 2 y1 …..
k yi
1 j Ckj y i k j
y2 …..
k!
….
j
Ck
k j ! j!
20.
Первый интерполяционный многочлен Ньютона дляравноотстоящих узлов
y0
x x0
Pn ( x) y0
h
2
y0
2!h
n
x x0 x x1 ...
2
y0
n!h
x x0 x x1 .... x xn 1
n
Используется тогда, когда точка, в которой требуется
вычислить приближенное значение функции находится
вблизи точки х0
21.
x x0t
h
f ( x) Pn ( x) Pn ( x0 th)
t (t 1) 2
y0 t y0
y0 ...
2!
t (t 1)...(t n 1) n
y0
n!
Первая интерполяционная формула Ньютона.
Используется для интерполирования вперед и экстраполирования
назад.
22.
Второй интерполяционный многочлен Ньютона дляравноотстоящих узлов
yn 1
x xn
Pn ( x) yn
h
2 yn 2
2!h
n
2
x xn x xn 1 ...
y0
n!h
x xn x xn 1 .... x x1
n
Используется тогда, когда точка, в которой требуется
вычислить приближенное значение функции находится
вблизи точки хп
23.
x xnq
h
f ( x) Pn ( x) Pn ( xn qh)
q (q 1) 2
yn q yn 1
yn 2 ...
2!
q (q 1)...(q n 1) n
y0
n!
Вторая интерполяционная формула Ньютона.
Используется для интерполирования назад и экстраполирования
вперед.
24.
( n 1)( )
x x0 x x1 .... x xn
Rn ( x)
n 1 !
f
n 1
y0
Rn ( x)
t (t 1)...(t n 1)
n 1 !
n 1
y0
Rn ( x)
q(q 1)...(q n 1)
n 1 !

























































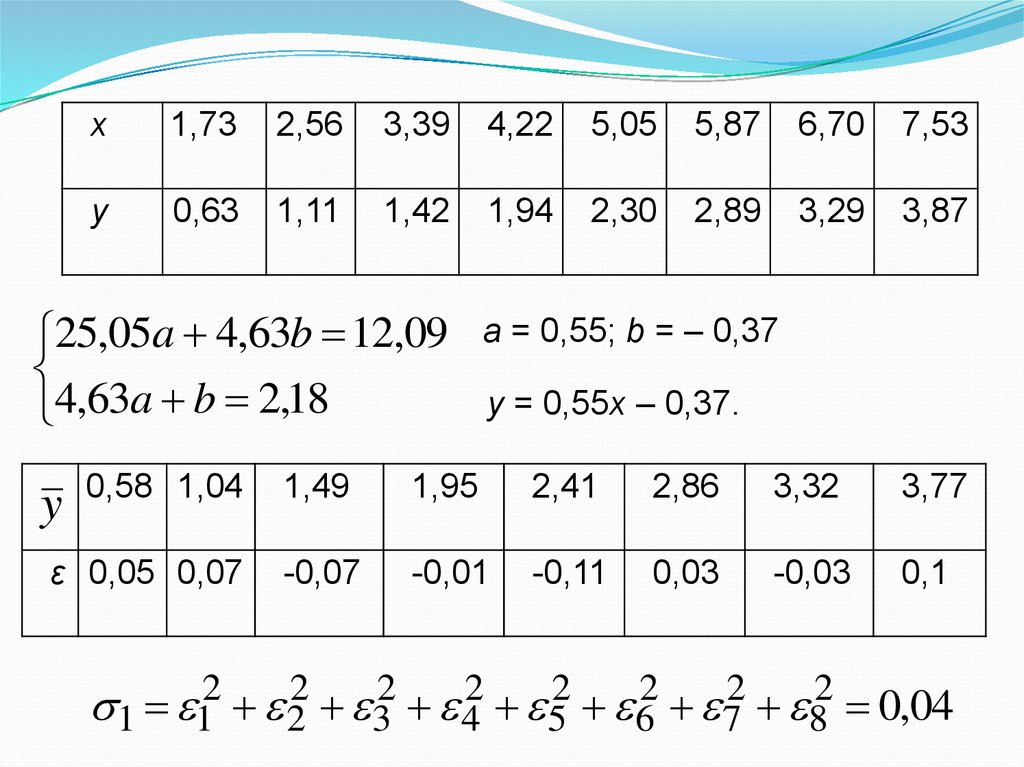
 Математика
Математика








