Тела вращения. Задачи на вычисление объёмов и площади поверхности

1.

Муниципальное казенное общеобразовательное учреждение
Задачи по теме
«Тела вращения»
на вычисление объёмов и площади поверхности
Выполнила:
учитель математики
2020 г

2.

Содержание
Цилиндр
Конус
Шар
Базовый уровень
(задания ЕГЭ базовый №16)
Повышенный уровень
(задания ЕГЭ профильный №8)
Высокий уровень
(задания ЕГЭ профильный №14)

3.

МЕНЮ
Базовый уровень
(задания ЕГЭ базовый №16)
Vц S
б.п.ц
Старт/стоп
Vк
S
п.ш
Vш S
б.п.к

4.

Каталог
заданий
Объем цилиндра (Vц)
Справк
а
Даны два цилиндра. Радиус основания и высота первого равны
соответственно 2 и 6, а второго — 6 и 7.
Во сколько раз объём второго цилиндра
больше объёма первого?
Решение
Объём цилиндра находится по формуле:
Найдём объём первого цилиндра:
Найдём объём второго цилиндра:
Найдём отношение объёма второго шара к первому:
Решение
Ответ: 10,5.
Ответ

5.

Каталог
заданий
Площадь боковой поверхности
цилиндра (Sб.п.ц)
Справка
Даны два цилиндра. Радиус основания и высота первого равны
соответственно 4 и 18, а второго — 2 и 3.
Во сколько раз площадь боковой поверхности
первого цилиндра больше площади
боковой поверхности второго?
Решение
Площадь боковой поверхности цилиндра
находится по формуле:
Найдём Sб.п первого цилиндра:
Найдём Sб.п второго цилиндра:
Найдём отношение площади боковой поверхности
цилиндра первого цилиндра ко второму:
Решение
Ответ: 12
Ответ

6.

МЕНЮ
Цилиндр
Цилиндр – тело, ограниченное
цилиндрической поверхностью и двумя
кругами.
Объем цилиндра (с
радиусом основания R и
высотой H):
S - площадь основания цилиндра, h - высота цилиндра,
π - число пи (3.1415), r - радиус цилиндра,
Площадь боковой и полной поверхностей цилиндра:

7.

Каталог
заданий
Объем конуса (Vк)
Справка
Объем конуса равен 16. Через середину высоты
параллельно основанию конуса проведено
сечение, которое является основанием меньшего
конуса с той же вершиной. Найдите объем
меньшего конуса.
Решение
Меньший конус подобен большему с коэффициентом 0,5.
Объемы подобных тел относятся как куб коэффициента
подобия. Поэтому объем меньшего конуса в восемь раз
меньше объема большего конуса.
Решение
Ответ: 2.
Ответ

8.

Каталог
заданий
Площадь боковой поверхности
конуса (Sб.п.к)
Справка
Во сколько раз уменьшится площадь боковой поверхности
конуса, если радиус его основания уменьшится в 1,5 раза, а
образующая останется прежней?
Решение
Площадь боковой поверхности конуса равна
При уменьшении радиуса основания в 1,5 раза при неизменной
величине образующей площадь боковой поверхности тоже
уменьшится в 1,5 раза.
Решение
Ответ: 1,5
Ответ

9.

МЕНЮ
Конус
Ко́нус —
тело, которое состоит из круга –
основания конуса, точки, не лежащей в
плоскости этого круга, - вершины конуса и всех
отрезков, соединяющих вершину конуса с точками
основания.
Объем конуса (с радиусом
основания R и высотой H):
Площадь боковой поверхности конуса равна:
где R — радиус основания, l — длина образующей.

10.

Каталог
заданий
Объем шара (Vш)
Справка
Даны два шара с радиусами 4 и 1. Во сколько раз объём
большего шара больше объёма другого?
Решение
Найдём отношение объёмов шаров:
Решение
Ответ: 64.
Ответ

11.

Каталог
заданий
Площадь поверхности
Справка
шара (Sш)
Даны два шара с радиусами 9 и 3. Во сколько раз площадь
поверхности большего шара больше площади поверхности
меньшего?
Решение
Площади шаров относятся как квадраты их радиусов,
следовательно, площадь поверхности второго шара в
раз
больше площади поверхности первого.
Решение
Ответ: 9
Ответ

12.

МЕНЮ
Шар
Шар — геометрическое тело,
ограниченное поверхностью, все
точки которой отстоят на равном
расстоянии от центра. Это
расстояние называется радиусом
шара.
Объем шара (с радиусом
основания R ):
4
3
S R
3
Площадь поверхности шара:
S 4 R
2

13.

МЕНЮ
Повышенный уровень
(задания ЕГЭ профильный №8)
Vц S
б.п.ц
Старт/стоп
Vк
S
п.ш
Vш S
б.п.к

14.

Каталог
заданий
Объем цилиндра (Vц)
Справка
Шар, объём которого равен 42, вписан в цилиндр. Найдите
объём цилиндра.
Решение
Высота цилиндра равна двум радиусам вписанного в цилиндр шара, поэтому
объем цилиндра, выраженный через радиус вписанного в него шара, даётся
формулой
Объём шара вычисляется по формуле
откуда имеем:
Тем самым, объём цилиндра равен 63.
Решение
Ответ: 63
Ответ

15.

Каталог
заданий
Площадь боковой поверхности
цилиндра (Sб.п.ц)
Справка
Длина окружности основания цилиндра равна 3,
высота равна 2. Найдите площадь
боковой поверхности цилиндра.
Решение
Площадь боковой поверхности цилиндра равна:
где C – длина окружности основания. Поэтому
Решение
Ответ: 6
Ответ

16.

Каталог
заданий
Объем конуса (Vк)
Справка
Цилиндр и конус имеют общие основание и высоту.
Объём цилиндра равен 18. Найдите объём конуса.
Решение
Поскольку, конус и цилиндр имеют общую высоту и основание, имеем:
Решение
Ответ: 6.
Ответ

17.

Каталог
заданий
Справка
Площадь боковой поверхности
конуса (Sб.п.к)
Длина окружности основания конуса равна 3,
образующая равна 2. Найдите площадь
боковой поверхности конуса.
Решение
Площадь боковой поверхности конуса равна
,
где С — длина окружности основания, а l — образующая. Тогда
Ответ: 3
Решение
Ответ

18.

Каталог
заданий
Объем шара (Vш)
Справка
Цилиндр описан около шара. Объем цилиндра равен 33.
Найдите объем шара.
Решение
Выразим из формулы для объёма цилиндра
подставим в формулу для объёма шара
Решение
Ответ: 22
и
Ответ

19.

Каталог
заданий
Площадь поверхности
Справка
шара (Sш)
Даны два шара. Радиус первого шара в 2 раза
больше радиуса второго. Во сколько раз площадь
поверхности первого шара больше площади
поверхности второго?
Решение
Площадь поверхности шара выражается через его радиус
формулой
, поэтому при увеличении радиуса
вдвое площадь увеличится в 22 = 4 раза.
Решение
Ответ: 4
Ответ

20.

МЕНЮ
Высокий уровень
(задания ЕГЭ профильный №14)
Vц S
б.п.ц
Старт/стоп
Vк
S
п.ш
Vш S
б.п.к

21.

Каталог
заданий
Объем цилиндра (Vц)
Справка
В цилиндре образующая перпендикулярна плоскости
основания. На окружности одного из оснований
цилиндра выбраны точки A, B и C, а на окружности
другого основания — точка C1, причём CC1 —
образующая цилиндра, а AC — диаметр
основания. Известно, что
,
.
а) Докажите, что угол между
прямыми AC1 и BC равен
.
б) Найдите объём цилиндра.
Решение
Ответ:
Ответ

22.

Решение
а) Пусть BB1 — образующая цилиндра. Тогда BB1C1C — прямоугольник,
поэтому угол между прямыми AC1 и BС равен углу
.
Угол ABC опирается на диаметр основания цилиндра,
поэтому он прямой. Значит, прямая B1C1, параллельная
прямой BС, перпендикулярна прямым AB и BB1.
Таким образом, прямая B1С1 перпендикулярна плоскости ABB1,
а значит, угол AB1C1 прямой. В прямоугольном треугольнике АB1С1:
Значит,
б) Отрезок AC является диаметром основания цилиндра. Значит,
площадь основания цилиндра
Следовательно, объём цилиндра

23.

Каталог
заданий
Площадь боковой поверхности
цилиндра (Sб.п.ц)
Справка
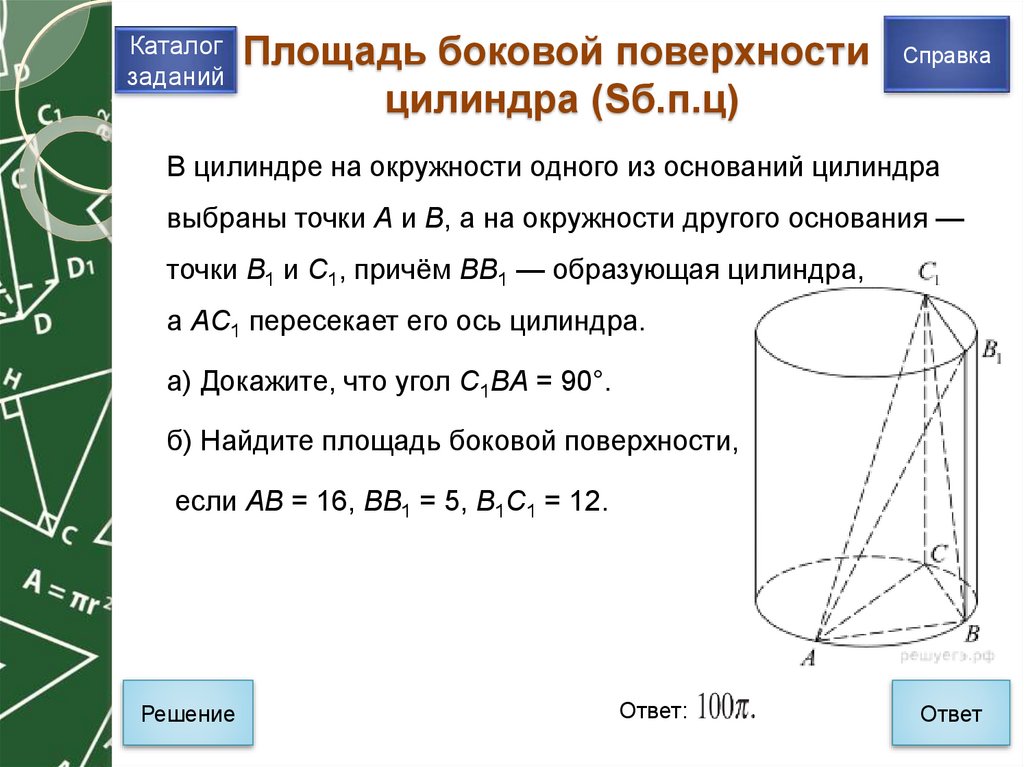
В цилиндре на окружности одного из оснований цилиндра
выбраны точки A и B, а на окружности другого основания —
точки B1 и C1, причём BB1 — образующая цилиндра,
а AC1 пересекает его ось цилиндра.
а) Докажите, что угол C1BA = 90°.
б) Найдите площадь боковой поверхности,
если AB = 16, BB1 = 5, B1C1 = 12.
Решение
Ответ:
Ответ

24.

Решение
а) Пусть точка C проекция точки C1 на нижнее основание.
Тогда AC — проекция AC1 на плоскость нижнего основания. Так
как AC1 пересекает ось цилиндра, то и AC тоже.
Следовательно, AC является диаметром окружности,
а
так как опирается на него. CB является
проекцией C1B. Тогда C1B перпендикулярно AB по теореме о
трёх перпендикулярах, то есть
б)
Тогда по теореме Пифагора для
треугольника гипотенуза
Следовательно,

25.

Каталог
заданий
Объем конуса (Vк)
Справка
Конус вписан в шар. Радиус основания конуса равен
радиусу шара. Объем шара равен 28. Найдите
объем конуса.
Решение
Запишем формулу для объёма шара:
Объём конуса в 4 раза меньше:
Решение
Ответ: 7.
Ответ

26.

Каталог
заданий
Площадь боковой поверхности
конуса (Sб.п.к)
Справка
Цилиндр и конус имеют общие основание и высоту. Высота
цилиндра равна радиусу основания. Площадь боковой
поверхности цилиндра равна
Найдите площадь боковой поверхности конуса.
Решение
Конус и цилиндр имеют общую высоту и равные радиусы
основания. Площадь боковой поверхности цилиндра
равна
откуда, учитывая, что
получаем:
или
Образующая конуса l , его высота h и радиус r
основания связаны соотношением
что
получаем:
поверхности конуса равна
Решение
или
откуда, учитывая,
Площадь боковой
следовательно:
Ответ: 3
Ответ

27.

Каталог
заданий
Объем шара (Vш)
Справка
Цилиндр описан около шара. Объем цилиндра равен 33.
Найдите объем шара.
Решение
Выразим из формулы для объёма цилиндра
подставим в формулу для объёма шара
Решение
Ответ: 22
и
Ответ

28.

Каталог
заданий
Площадь поверхности
Справка
шара (Sш)
Объем первого шара в 27 раз больше объема второго. Во
сколько раз площадь поверхности первого шара больше
площади поверхности второго?
Решение
Найдем отношение объемов шаров:
,
откуда Площади их поверхностей соотносятся как квадраты
радиусов:
Решение
Ответ: 9
Ответ

29.

Список использованной
литературы
Ссылки на задачи из сайта https://math-ege.sdamgia.ru/
https://mathb-ege.sdamgia.ru/problem?id=509741
https://mathb-ege.sdamgia.ru/problem?id=511620
https://ege.sdamgia.ru/problem?id=27052
https://ege.sdamgia.ru/problem?id=27137
https://mathb-ege.sdamgia.ru/problem?id=509681
https://mathb-ege.sdamgia.ru/problem?id=520727
https://ege.sdamgia.ru/problem?id=525041
https://ege.sdamgia.ru/problem?id=27133
https://ege.sdamgia.ru/problem?id=27133
https://ege.sdamgia.ru/problem?id=269371
https://ege.sdamgia.ru/problem?id=27135
https://ege.sdamgia.ru/problem?id=245348
https://ege.sdamgia.ru/problem?id=27072
https://ege.sdamgia.ru/problem?id=520784
https://ege.sdamgia.ru/problem?id=520869
https://ege.sdamgia.ru/problem?id=245351
https://ege.sdamgia.ru/problem?id=324458
https://ege.sdamgia.ru/problem?id=245348
https://ege.sdamgia.ru/problem?id=27162