Қосалқылық теоремасының негізінде сызықтық бағдарламалау есебінің шығарылуын түсіндіріңіз

1.

6.
ҚОСАЛҚЫЛЫҚ ТЕОРЕМАСЫНЫҢ НЕГІЗІНДЕ СЫЗЫҚТЫҚ
БАҒДАРЛАМАЛАУ ЕСЕБІНІҢ ШЫҒАРЫЛУЫН ТҮСІНДІРІҢІЗ
Қос мәселе деп тікелей есеп шарттарынан белгілі бір ережелерді
қолдана отырып тұжырымдалған көмекші сызықтық бағдарламалау есебі
түсініледі.
Тікелей және қос сызықтық бағдарламалау есептері
Экономикалық тұрғыдан екі жақты мәселені келесідей түсіндіруге
болады: ресурстардың bi мөлшеріне және бірліктің мәндеріне шығындардың
жалпы құнын барынша азайту үшін ресурстардың әрқайсысының бірлік
бағасы қандай болуы керек құны Cj? Ал біз бастапқы есепті келесідей
анықтаймыз: берілген шығындар үшін Cj (j = 1,2, ..., n) болатындай етіп xj (j =
1,2, ..., n) қанша және қандай өнім шығару керек. ) өнім бірлігі және қолда бар
ресурстар мөлшері bi (i = 1,2,…, n). Сызықтық бағдарламалау мәселелерінің
көпшілігі бастапқыда екі немесе екінші есептер ретінде анықталады.
Қорытынды жасай отырып, біз екі сызықтық бағдарламалаудың жұбы туралы
айтуға болады.
Әрбір сызықтық бағдарламалау есебін белгілі бір жолмен бастапқы
немесе тікелей есепке қатысты қосарланған немесе конъюгат деп аталатын
басқа (сызықтық бағдарламалау) есептермен байланыстыруға болады. Жалпы
сызықтық бағдарламалау мәселесіне қатысты қос есептің анықтамасын
берейік, ол біз білетініміздей, функцияның максималды мәнін табу керек:
жағдайында

2.

Екі тұжырымдалған тапсырманы салыстыра отырып, қос тапсырма
келесі ережелерге сәйкес жасалғанын көреміз:
1 Бастапқы есептің мақсаттық функциясы максимумға, ал дуальдың
минималды функциясы орнатылған.
2 Матрица
бастапқы есеп жүйесіндегі белгісіз шектеулер коэффициенттерінен
және ұқсас матрицадан тұрады
қос есепте олар бір-бірінен транспозиция арқылы алынады (яғни
жолдарды бағандармен, ал бағандарды жолдармен ауыстыру).
3. Қос есепте айнымалылар саны бастапқы есеп жүйесіндегі шектеулер
санына тең, ал қос есептер жүйесіндегі шектеулер саны бастапқы есептердегі
айнымалылар санына тең.
төрт. Қос есептің объективті функциясындағы белгісіздердің
коэффициенттері - бұл бастапқы есеп жүйесіндегі бос терминдер, ал қос
есептер жүйесінің қатынастарындағы оң жақтары - белгісіздердің
коэффициенттері. түпнұсқа мәселе.
5 Егер бастапқы есептің xj айнымалысы тек оң мәндерді қабылдай алса,
онда қос есептер жүйесіндегі j-ші шарт «>» түріндегі теңсіздік болып
табылады. Егер xj айнымалысы оң және теріс мәндерді де қабылдай алса,
онда 1 - жүйедегі қатынас теңдеу болады. Ұқсас байланыстар бастапқы
есептің шектеулері мен қос есептің айнымалылары арасында орын алады.
Егер i - бастапқы есеп жүйесіндегі қатынас теңсіздік болса, онда қос есептің
i-ші айнымалысы
... Әйтпесе, уj айнымалысы оң және теріс мәндерді де
қабылдай алады.
Қос есепті жұптар әдетте симметриялы және асимметриялы болып
бөлінеді. Қос есептердің симметриялы жұбында тура есептің шектеулері мен
қос есептердің қатынастары форманың теңсіздіктері болып табылады «.
Сонымен, екі есептің де айнымалылары тек теріс емес мәндерді қабылдай
алады.
Қос есеп сызықтық бағдарламалау мәселесімен тығыз байланысты.
Бастапқы тапсырма алғашқы деп аталады. Қос есепті шешуді шешуден
бастапқыға дейін және керісінше алуға болады. Осы екі есептің
байланыстырушы фактісі - бастапқы есептің функциясының Cj

3.

коэффициенттері. Бұл коэффициенттерді қос есептердің шектеулер жүйесінің
еркін мүшелері деп атайды. Бастапқы есептің шектеулер жүйесінің Bi
коэффициенттері қос есептердің коэффициенттері деп аталады. Бастапқы
есептің шектеу жүйесінің коэффициенттерінің ауыстырылған матрицасы қос есептердің шектеулер жүйесінің коэффициенттерінің матрицасы.
Ресурстарды пайдалану проблемасын қарастырыңыз... Кәсіпорында b (i
= 1, 2,…, m) бірлік көлеміндегі ресурстардың t түрі бар, олардың ішінде
өнімнің n түрі шығарылады. 1 дана дайындау үшін. I-ші өнім aij бірлігіне
жұмсалады. t-ші ресурс, оның құны Cj бірлік. Құндық мәнде оның
максималды шығуын қамтамасыз ету үшін өндіріс жоспарын анықтау қажет.
Xj (j = 1,2,…, n) бірлік санын алайық. j-ші өндіріс және бұл сызықтық
функцияның максималды мәні
Z=C1x1+C2x2+ … +Cnxn

4.

Тауарларды өндіруге қажет ресурстарды анықтайық. Өндірілген
тауарлар құнының бірлігін ресурстар құнының бірлігі ретінде белгілейік. Ал
уi арқылы (j = 1,2, ..., m) i-ші ресурс бірлігінің құны. Анау. j-ші өнімнің
бірлігін ойлап табуға қолданылатын барлық жұмсалған ресурстардың құны.
Шығындалған ресурстардың бағасы түпкілікті өнімнің бағасынан аспауы
керек.
Қосарлық теореманың негіздері
Асимметриялық қос есептер
Дуальдық теоремасы:
Асимметриялық қос есептердегі бастапқы есептің шектеулер жүйесі
теңдік ретінде анықталады. Қос есеп теңсіздік ретінде көрсетілген, ал
айнымалылар теріс болуы мүмкін. Есептерді түсінуді жеңілдету үшін оны
матрица түрінде түсіндіреміз.
Қос мәселені тұжырымдап көрейік. f=YA0 сызықтық функциясын
көбейтетін және шектеулерді қанағаттандыратын Y=(y1, y2,…, ym), қатар
матрицасын анықтау керек.
YA> C (1.1)
Бастапқы мәселені тұжырымдап көрейік. Z = CX және сызықтық
функциясын минимизациялайтын X = (x1, x2,…, xn) баған матрицасын
анықтаңыз. шектеулерді қанағаттандырады
AX = A0, X> 0 (1.2)
Бастапқыда да, қос есептерде де A = (aij) - шектеу жүйесінің
коэффициенттерінің матрицасы, A0 = (b1, b2, ..., bm) - баған матрицасы, C =
(c1, c2) , ..., cn) - қатар матрицасы ... Қосарлық теорема қос есептердің
жұптарының оңтайлы жобалары арасында байланыс орнатады.
Екіұдайлық теоремасы айтады: егер қос есептердің бірінің оңтайлы
дизайны болса, онда екіншісінің шешімі бар, ал сызықтық функциялардың
шекті мәндері үшін minZ = maxf қатынасы орындалады. Егер есептердің
біреуінің сызықтық функциясы шектелмеген болса, онда екіншісінің шешімі
болмайды
Дәлелдемелер.
Біз бастапқы проблеманың оңтайлы жоспары бар деп есептейміз.
Жоспар симплекс әдісі арқылы анықталады. Ақырлы негіз A1, A2,…, Am
алғашқы m векторларынан тұрады деп болжауға болады.
Біз D - ақырлы негіз A1, A2., Am векторларының компоненттерінен
құралған матрица деп есептейміз. Жоғарыдағы кесте A1, A2, ..., An
векторларының кеңею коэффициенттерінен тұрады жүйе базистік векторлар
тұрғысынан. Бұл кестеде әрбір A j векторы Xj векторына сәйкес келеді.
(1.3) және (1.4) қатынастарын қолдана отырып:
(1.5) A=D, D-1A=
(1.6) A0 =DX*; D-1A0 =X
(1.7) min Z= C*X*,
(1.8) = C* – C > 0,

5.

мұндағы С=(C1, C2,…, Cm), С=(C1, C2,…, Cm, Cm +1,…, Cn), a=(CX1–C1;
СХ2 – С2,…, CXn–Cn)=(Z1–С; Z2-C2;…, Zn–Cn) - вектор, оның компоненттері оң
емес, өйткені олар оңтайлы дизайнға сәйкес келетін Zj - Cj> 0 сәйкес келеді.
Бастапқы есептің оңтайлы жоспары X = D-1A0 түріне ие, сондықтан
қос есептердің оңтайлы жоспарын формадан іздейміз
(1.9) Y = C*D-1
Y * шынымен де қос есептің жоспары екенін көрсетейік. Осы шектеу
үшін (1.2) біз YA-C> 0 теңсіздігі түрінде жазамыз, сол жағында Y *
ауыстырамыз. Содан кейін (1.9), (1.5) және (1.8) негізінде аламыз
YА–С=С*D-1А–С=С-С>0, қайдан Y * A> С табамыз
Y * шектеулерді қанағаттандыратындықтан (1.2), бұл қос есептің
жоспары. Осы дизайн бойынша f(Y)=Y*A0 қос есебінің сызықтық
функциясының мәні. (1.9), (1.6) және (1.7) қатынастарын ескере отырып,
бізде
(1.10) f (Y) = Y*A0=C * D-1A0= C*X = minZ(X)
Сонымен, қос есептің сызықтық функциясының мәні Y-де сандық
тұрғыдан бастапқы есептің сызықтық функциясының минимумына тең
болады
Дәлелдейікенді Y * - бұл оңтайлы жоспар. Біз (1.1) қос есептің кезкелген Y жоспарына, ал (1.2) - бастапқы есептің кез-келген X жоспарына
көбейтеміз: YAX=YA0=f(Y), YAX>СХ=Z(X), демек, кез келген X және Y
теңсіздіктер жоспарлары
(1.11) f (Y)> Z (X)
Дәл осы қатынас maxf (Y)> minZ (X) шекті мәндеріне де қатысты.
Соңғы теңсіздіктен, сызықтық функцияның максималды мәні maxf (Y) =
minZ (X) болғанда ғана қол жеткізіледі деген қорытындыға келеміз, бірақ бұл
f (Y) мәні Y дизайнына жетеді, сондықтан Y дизайны оңтайлы жобалау
болып табылады қос мәселе.
Сол сияқты, егер қос есепте шешім болса, онда түпнұсқада да шешім
және maxf (Y) = minZ (X) қатынаста болатындығын дәлелдеуге болады
Теореманың екінші бөлігін дәлелдеу үшін бастапқы есептің сызықтық
функциясы төменнен шектелмеген деп есептейміз. Сонда (1.11) -дан f (Y) - Y
болатындығы шығады. Бұл өрнек мағынасыз, сондықтан қос есептің
шешімдері жоқ.
Сол сияқты, қос есептің сызықтық функциясы жоғарыда шектелмеген
деп есептейміз. Онда (1.11) -тен Z (X) + Y болатынын аламыз. Бұл өрнек те
мағынасыз, сондықтан бастапқы проблеманың шешімі жоқ.
Дәлелденген теорема қос есептердің бірін шешкен кезде екіншісінің
оңтайлы жоспарын табуға мүмкіндік береді. Мұнда жол матрицасы С = (0; 1;
0; –1; - 3, 0), баған матрицасы
1 1 2 0 -1 1 0
A 0 = 2 A = 0 -4 1 2 -1 0

6.

3030011
100
2 -4 3
A «’ = 0 1 0
-1 2 0
1 -1 0
001
Қос тапсырма. Шектеулерге тәуелді
функциясының максималды мәнін табыңыз
y1> 0
f=y1+2y2+5y3
сызықтық
2y1 – 4y2 + 3y3 > 1,
y2 > 0,
(-y1) + 2y2 >(-1),
y1 – y2 + y3 = -3, y3 > 0
Бастапқы есептің оңтайлы жоспары - X = (0; 1/3; 0; 11/3; 4; 0), ол үшін
Zmin = -46/3 аламыз. Осы қайталануды қолдана отырып, қос есептердің
оңтайлы жоспарын табамыз. Екілік теоремасына сәйкес, қос есептің оңтайлы
жоспары Y= C*D-1, қатынасынан табылады, мұндағы D-1 матрицасы векторлардың құрамына кіретін матрицаға матрицаға кері матрица. негіз, ол
үшін бастапқы есептің оңтайлы жоспары алынады. Соңғы негізге A5, A4, A2
векторлары кіреді; білдіреді,
1 -1 2
D = (A 5, A 4, A 2) = -1 2 -4
103
Кері матрица D -1 төртінші қайталанудың A1, A3, A6 бағандарындағы
коэффициенттерден құрылады:
210
D -1 = -1/3 1/3 2/3
-2/3 -1/3 1/3
Сол қайталаудан С = (–3; –1; 1) шығады. Осылайша
210
Y=С*D-1 =(-3; – 1; 1) -1/3 1/3 2/3
-2/3 1/3 1/3
Y=(-19/3; – 11/3; – 1/3),

7.

анау. yi = С * Хi, мұндағы Хi - бастапқы бірлік негізінің векторларының
бағандарында орналасқан соңғы қайталанудың кеңею коэффициенттері.
Сонымен, i-ші қос айнымалыны бастапқы бірлік негізіне кіретін сәйкес
векторға қарама-қарсы тұрған бағалау мәнінен (m + 1) - ші қатардан алуға
болады, егер оған коэффициенттің сәйкес мәнін қоссақ сызықтық функция:
у1 =–19/3+0=–19/3; y2 =-11/3+0=-11/3; у3 =-1/3+0=-1/3
Осы жоспармен maxf = -46 / 3

8.

Симметриялық қос есептер
Екі сызықтық бағдарламалау есептерінің бір түрі - бұл екіге тең
симметриялы есептер, онда бастапқы және қос есептер үшін шектеулер
жүйесі теңсіздіктермен беріледі, ал қос айнымалыларға теріс емес шарт
қойылады.
Бастапқы тапсырма. Шектеу жүйесін қанағаттандыратын X = (x1, x2,…,
xn) баған матрицасын табыңыз
(1.12). AX> A0, X> 0 және Z = CX сызықтық функциясын азайтады
Қосымша айнымалыларды пайдаланып, теңсіздіктер жүйесін теңдеулер
жүйесіне айналдыруға болады, сондықтан симметриялы қос есептердің кезкелген жұбы асимметриялық есептер жұбына айналуы мүмкін, ол үшін екі
жақтылық теоремасы әлдеқашан дәлелденген.
Симметрияны қолдану арқылы шешуге ыңғайлы есепті таңдауға
болады. Компьютер шешетін есептің көлемі енгізілген сызықтар санымен
шектеледі, сондықтан бастапқы жағдайда едәуір ауыр болатын мәселені
қосарланған тұжырымдауда жеңілдетуге болады. Машиналардың көмегінсіз
есептеулерде қосарлы қолдану есептеуді жеңілдетеді.
Қос есепті жазу үшін алдымен формулаға бастапқы есептің шектеулер
жүйесін келтіру керек екені анық. Ол үшін екінші теңсіздікті -1-ге көбейту
керек.
Қос есептердің математикалық модельдерінің түрлері
Қарастырылған асимметриялық және симметриялық қос есептерге
сүйене отырып, математикалық модельдердің қос есептерінің жұптарын
келесі түрде ұсынуға болатындығын ескереміз:
Симметриялық тапсырмалар
(1) Бастапқы мәселе Қос мәселе
Zmin=CX; fmax =Y>A0;
AX=A0; YA=С
X>0 Y>0
(2) Бастапқы мәселе Қос мәселе
Zmax =CX; fmin =YA0;
AX=A0; YA=С
X>0 Y>0
Асимметриялық тапсырмалар
(3) Қос проблема
Zmin=CX; fmax=YA0;
AX=A0; YA=С

9.

X>0
(4) Бастапқы проблема Қос мәселе
Zmax=CX; fmin=YA0;
AX=A0; YA=С
X>0
Демек, берілген бастапқы есеп үшін қос есепті тұжырымдамас бұрын,
бастапқы есептің шектеулер жүйесін дұрыс түрлендіру керек.
1.4 Екі жақты симплекс әдісі
Бастапқы проблеманың шешімін алу үшін сіз екіге баруға болады.
Оның оңтайлы жоспарының бағаларын қолдана отырып, сіз бастапқы есептің
оңтайлы шешімін анықтай аласыз.
Егер бірлік симплексті негізі бар бірінші симплекстік кестені
қарастыратын болсақ, онда қос мәселеге көшудің қажеті жоқ. Бұл бағандарда
бастапқы есеп, ал жолдарда қос есептеулер анықталғандығына байланысты.
bі - қосарланған проблемалық жоспардың бағалары. Сj - бастапқы
проблемалық жоспардың бағалары.
Симплекс кестесін пайдаланып, қос есепті шешуді табайық. Түпнұсқа
есеп симплекс кестесінде жазылған. Біз қосарланған проблеманың оңтайлы
жоспарын да анықтаймыз. Біз сондай-ақ бастапқы проблеманың оңтайлы
жоспарын табамыз.
Бұл әдісті әдетте қос симплекс әдісі деп атайды.
Жалпы формада қойылған бастапқы сызықтық бағдарламалау
мәселесін анықтау керек делік: AX = A0, X> 0 кезіндегі Z = CX функциясын
азайту үшін. Демек, қос есепте f = YA0 функциясы YA> S үшін максималды
болуы керек. Келесі негіз D = (A1, A2,…, Ai,…, Am) анықталсын, ал ондағы
X = D-1A0 = (x1, x2,…, xi,… векторының компоненттерінің кем дегенде
біреуі) , xm) теріс. Барлық Aj векторлары үшін Zj - Cj> 0 (i = 1,2,…, n)
қатынасы қолданылады.
Екілік теоремасын қолдана отырып, Y = CbazD-1 екі жақты есеп
жоспары болып табылады. Бұл жоспар оңтайлы емес. Себебі қос есептің
оңтайлы жоспарының бағалары теріс болмауы керек және таңдалған Х
негізде теріс компонент болады және ол бастапқы есептің жоспары емес,
екінші жағынан.
Демек, xi <0 компонентіне сәйкес келетін Аi векторын бастапқы есептің
негізінен шығару керек. Бұл вектор теріс бағалауға сілтеме жасайды, оны қос
есептің негізіне қосу керек.
Біз i-ші қатарды бастапқы есептің негізінде қосылатын векторды таңдау
үшін қарастырамыз. Анау. егер қатарда xij <0 болмаса, онда қос есептің
сызықтық функциясы шешім политопында шектелмеген. Сондықтан
бастапқы проблеманың шешімдері жоқ.

10.

Әйтпесе теріс мәндері бар бағандар үшін q0j = min (xi / xij)> 0
анықтаймыз. Сондай-ақ, бастапқы максималды есепті шешкен кезде minq0j
(Zj - Cj) сәйкес келетін векторды табамыз, сонымен бірге maxq0j (Zj - Cj)
минималды есептің мәні болғанда.
Табылған вектор бастапқы есептің негізіне енгізілген. Бағыт сызығы
бастапқы есептің негізінде жойылатын векторды анықтайды.
Айталық, q0j = min (xi / xij) = 0, яғни. xi = 0, онда xij шешуші элемент
ретінде таңдалады, бірақ тек xij> 0 болған жағдайда.
Мәселені шешуге бұл тәсіл X векторының теріс компоненттерінің
көбеюіне әкелмейді, X> 0 алынғанша, процесс тоқтамайды.
Қос есептің оңтайлы жоспарын анықтай отырып, біз бастапқы есептің
оңтайлы жоспарын да табамыз.
Шешімде қос симплекс әдісінің алгоритмін қолданып, Zj - Cj> 0
шартын барлық хi <0 алынып тасталмайынша елемеуге рұқсат етіледі.
Оңтайлы жоспар әдеттегі симплекс әдісі арқылы анықталады. Бұл әдіс
әдетте барлық xi <0 болған жағдайда қолданылады. Бастапқы жоспарға өту
үшін бір итерациядағы есепті q0j = max (xi / xij)> 0 деп анықтау керек.
Сызықтық бағдарламалау есептерін қос симплекс әдісі арқылы шешуге
болады. Оң негізі бар мәселелердегі шектеулер жүйесі кез-келген белгінің
еркін шарттарына ие. Екі жақты симплекс әдісі симплекс кестесінің өлшемін
және шектеу жүйесінің түрлендірулер санын едәуір азайта алады.
7.
ЛОГИСТИКАДАҒЫ ҚОРЛАРДЫ БАСҚАРУ
НЕГІЗІНДЕ
ҚОРЛАРДЫ
БАСҚАРУ
СИПАТТАҢЫЗ(УИЛЛСОН МОДЕЛІ ЖАЗУ)
ТҮСІНІГІНІҢ
МОДЕЛІН
Жабдықтаушылармен жұмыс істеу кезінде әрдайым дилемма туындайды:
сирек тасымалдау есебінен үнемдейтін, бірақ сақтау және өлімге алып
келетін капиталды жоғалтатын үлкен партиялармен сатып алу керек пе, әлде
тапсырыспен және өңдеуге көбіне уақыт пен ақшаны жұмсай отырып сатып
алу керек пе?
Ол жұмыс істей ме, жоқ па?
Математика тауарларды сатып алуға, тапсырыс беруге және жөнелтуге,
сондай-ақ сақтауға кеткен шығындардың жалпы мөлшерін минимизациялай
отырып, тауарлар қорының оңтайлы деңгейін табуға мүмкіндік береді. Кезкелген математикалық модель сияқты, ол жұмыс істеу үшін тұрақты мәндерді
қажет етеді.
Сондықтан, бұл формула іс жүзінде қолданылады, бірақ жеткілікті және
тұрақты статистикасы бар тауарларға ғана, сұранысы тұрақты, осы модельдер
үшін форс-мажорлық жағдайлар сирек кездеседі. Шын мәнінде, біз осы
формула жұмыс істейтін тұрақты сұраныс тауарлары туралы айтып отырмыз.
Ресейлік логистикада осы модельді қолдануға қатысты даулар бар - бұл
қаншалықты өміршең? Тұрақты сұранысқа ие тауарлар үшін маңызды. Дереу
бронь жасайық: біз бұл формуланы қолданудың барлық аспектілерін
қарастырғымыз келмейді - ол бойынша оқулықтар мен ғылыми мақалалар

11.

жеткілікті. Бірақ біз ең бастысы - оның қалай жұмыс істейтінін және оны
қолдануды бастау үшін не қажет екенін қарастырамыз. Қарапайымнан
күрделіге қарай ұстанымын басшылыққа ала отырып, оны бір жеткізушінің
бір сатып алу тармағына қолданыңыз. Сонда сіз теорияны өз тәжірибеңізге
қалай кеңейту керектігін өзіңіз түсінесіз.
Модель дүкен жұмысы туралы жанама деректерді мұқият жинауды қажет
етеді. Нақтырақ айтқанда, Вильсон формуласын қолдануды бастамас бұрын
екі маңызды параметрді есептеу керек:
біріншісі - тапсырысты орналастыру құны (яғни тапсырыс берушіні
есептеуге, орналастыруға, жіберуге, қабылдауға және орналастыруға қанша
тұрады);
ал екіншісі - тапсырыстарды сақтауға кететін шығындар (яғни дүкен осы
өнімді қабылдауға, тіркеуге, сұрыптауға, сақтауға, буып-түюге, тасымалдауға
жұмсайтын сома).
Тапсырысты орналастыру құны
Тапсырысты орналастыру құны (кейде «толықтыру құны» деп аталады)
оларды орналастыру жиілігіне байланысты. Егер сатып алу бөлімінің
менеджері, мысалы, ыдыс-аяққа тапсырыс берсе, онда оның екі жиынтық
ыдысқа тапсырыс берудегі еңбек ақысы екі жүз жиынтыққа тапсырыс
беруден әлдеқайда аз болмайды. Тиісінше, тапсырысты орналастыру құны
неғұрлым аз болса, соғұрлым үлкен партияға тапсырыс беріледі.
Тапсырысты орналастыру құны, әдетте, келесі шығындарды қамтиды:
жеткізушіні іздеу (мысалы, көрмелерге бару);
келіссөздер жүргізу (опция ретінде, тіпті келіссөздер кезінде ішілген шай
мен кофе);
тапсырысты тіркеу және жіберу (сатып алу менеджерінің уақыты);
тасымалдауды қадағалау (менеджердің уақыты мен күші, кейде байланыс
шығындары);
қор қозғалысы туралы статистикалық ақпаратты талдау;
тапсырыс келген кезде оны қабылдау;
сапа талаптарын беру;
құжаттарды салыстыру;
тасымалдау, егер ол тауар бағасына кірмеген болса;
үшінші тарап ұйымдарының көлік тарифтерін төлеу;
көлік-тиеу-түсіру жұмыстарын жеткізуге шығындар;
жеткізушілердің шоттарын жүргізу және басқа шығындар.
Ең қолайлы, ең дәл емес әдіс - сатып алу бөлімінің жылдық
шығындарын (бөлім қызметкерлерінің жалақысы, материалдық және үстеме
шығындар, іссапарлар, келіссөздер мен презентация шығындары) жылына
берілген тапсырыстар санына бөлу. . Бұны жұмысшының нақты жұмыс
уақытымен және тапсырыстарды дайындауға және тапсыруға кететін орташа
уақытты анықтау мақсатында жүргізілген сауалнамамен салыстыруға болады.
МЫСАЛ. Көрнекі мысал ретінде жеке тапсырыс бойынша шығындар
есебін қарастырыңыз.

12.

Дүкен тұрмыстық техниканы сатып алады. Өнім тоңазытқыш. Жеткізу,
әдетте, шағын партиялармен жүзеге асырылды (4-5 дана). Тапсырысты
орналастыру және қабылдау құны жұмысқа тікелей қажет болатын
факторлардың құнынан тұрады:
1 фактор - сатып алу менеджерінің жұмысы;
фактор 2 - тауарларды қабылдайтын тиегіштің жұмысы;
фактор 3 - қабылдау үшін жабдықтың жұмысы (тиегіш, стекер);
4 фактор - тоңазытқышты орталық қоймадан желілік дүкендерге
тасымалдау.
ФАКТОР 1
Шығын коэффициенті - бұл сатып алу менеджері өткізген уақыт. Жалақы
= айына 800 доллар
Барлығы: $ 800/22/8 = $ 4,55 / сағ
1–20 тоңазытқышқа тапсырыс берудің орташа жұмыс уақыты 1,5 сағатты
құрайды.
Фактор құны: $ 4,55? 1,5 = 6,825 доллар.
ФАКТОР 2
Шығын коэффициенті - бұл қойма жұмысшысының жұмыс уақыты.
Жалақы = айына 400 доллар
Барлығы: айына 400/22 жұмыс күні / 8 сағат = 2,30 доллар / сағат.
1-5 тоңазытқышты қабылдау үшін қажетті уақыт - 20 минут.
Фактор құны: $ 2.30? 20/60 = 0,76 доллар
ФАКТОР 3
Факторлық шығындар жүк көлігінің амортизациясы мен техникалық
қызмет көрсету шығындарынан тұрады. Шығын коэффициенті - жүктеушінің
жұмыс уақыты. 5 жыл ішіндегі амортизацияның толық кезеңіне сүйене
отырып, коэффициенттің коэффициенті = $ 1, 00 / сағ. Қызмет шығындарын
есепке алу факторлық мөлшерлемені шамамен екі есеге арттырады.
Фактор құны: $ 1.00? 2? 20/60 = 0,70 доллар
ФАКТОР 4
Шығын коэффициенті - бұл қала ішіндегі тоңазытқышты тасымалдау
құны және «Газель» жүктерінің жұмыс уақыты. Бір сағаттық жұмыс құны 10 доллар, минималды жұмыс уақыты - 4 сағат + қызмет көрсету үшін 1
сағат, төрт тоңазытқышты қала бойынша екі дүкенге тасымалдау үшін 8 сағат
кетеді.
Бір тоңазытқыштың жеткізілімінің жалпы құны: $ 10 * 8/4 = $ 20.
Тапсырыс беру және қабылдау операцияларының жалпы құны: $ 6.825 +
$ 0.76 + $ 0.70 + $ 20 = $ 28.29.
Бір тоңазытқышты сатып алудың орташа құны (К): 28 доллар, 29/4 дана
= 7, 07 доллар.
Тәжірибе көрсеткендей, шығындар сметасындағы сәйкессіздік 5-10%
экономикалық тапсырыстың жалпы көлеміне айтарлықтай әсер етпейді.
Бір нәрсе маңызды: тапсырыс мөлшері неғұрлым үлкен болса (мысалы,
егер біз 4 данадан емес, 20 дан тұратын тоңазытқыштар партиясын әкелсек),
тапсырыс бізге арзанға түседі: K = 28 $, 29/20 дана = $ 1, 41.

13.

Сонымен, бізге көбірек әкелу керек пе?
Тапсырыстарды сақтау құны
Сақтау шығындарына қойма қорында тоңазытылған айналым
қаражаттарының құны, тауарларды қоймада ұстау шығындары және дүкенде
тауарлардың нақты болуымен байланысты басқа шығындар жатады. Бұған
мүлік салығы мен тауарлы-материалдық құндылықтарды сақтандыру,
жетіспеушілікке немесе шектеулі сақтау мерзіміне байланысты шығындар,
тарылу, тарылу, тауарлы-материалдық құндылықтарды сақтауға байланысты
шығындар (мысалы, орналасқан үй-жайларды жалға алу, жылыту, жарық
пайдалану үшін және т.б.) кіруі керек. .
Шығындарды есептеу жұмысын нақты нені есептеу керек екенін
түсіндіріп, бухгалтерияға тапсырған дұрыс:
капиталды шығындар немесе акцияларға салынған қаражаттарды
иммобилизациялау шығындары (капиталдан келетін шығындар қатып
қалады);
қойма жұмысымен байланысты қойма жұмысшылары мен жабдықтау
бөлімі қызметкерлерінің негізгі және қосымша жалақысы;
қойманың негізгі қорлары үшін төлем;
қойманы ұстауға арналған ағымдағы шығындар;
басқару персоналына еңбекақы төлеуге арналған шығыстар;
қабылдау кезінде тұтынылған материалдардың құны (қораптар,
гофрленген қаптама, созылған пленка);
сақталатын тауарлармен жүргізілетін жұмыс шығындары (орау,
сұрыптау, дүкенге көшу және т.б.);
табиғи шығындардан болатын шығындар;
сақтау нәтижесінде тауарлардың тұтынушылық қасиеттерінің
төмендеуінен болатын шығындар (тозу, тарылу, шайқас, презентацияның
жоғалуы және т.б.);
сақтандыру құны және салықтар.
Тауарлық-материалдық қорларды ұстауға кететін шығындарды нақты
есептеу қиын. Тауарлы-материалдық қорларды ұстауға кететін шығындар
тізімінің екі бөлігі - күрделі шығындар және тауарлы-материалдық
құндылықтарды ұстауға кететін шығындар - тауарлы-материалдық
құндылықтарды ұстауға кеткен шығындардың жалпы көлемінде ең үлкен
үлеске ие, өйткені тәуекел мен шығынның құны, әдетте, нақты есеп пен
жоспарлауға сәйкес келмейді.
МЫСАЛ. Сақтау шығындарының деңгейін (S) орташа шығындар әдісін
қолдана отырып анықтайық.

14.

«Жіберілген мүмкіндіктің құнын» 10% деп есептей отырып, біз
тауарлық-материалдық құндылықтарды ұстау құнын аламыз (фактор
ретінде):
S = 21600 (жалпы құны) / 335000 (түгендеудің жалпы құны) + 0, 10 = 0,
16
Акциялардың әр жүз рублі үшін қызмет көрсету құны 16 рубльді
құрайды. жылына немесе S = 16%.
Демек, аз әкелу керек шығар?
Экономикалық негізделген тәртіп
Біз көп емес, аз емес, бірақ өз шығындарымызды барынша азайтуға
мүмкіндік беретін мөлшерде әкелуіміз керек.
Уилсон моделі тауарлық-материалдық құндылықтар үшін өнімнің
оңтайлы санын табуға көмектеседі, бұл кезде оны өңдеуге және сақтауға
шығындар аз болады. Мұны «экономикалық негізделген тапсырыс» (EOQ,
немесе EOQ - экономикалық тапсырыс мөлшері) деп атайды.
FVC есептеу үшін сізге тапсырысты толтыру шығындарын (K), сақтау
шығындарын (S), күнделікті сұранысты (v), заттың сатып алу бағаларында
(ларында) бірлік құнын және тауардың жалпы күндер санын білуіңіз керек.
бір жылдан кейін сатылады (т).
Уилсонның моделі кейбір шектеулермен сипатталатын және келесі
шарттарға ие сатып алуды сипаттайды:
модель өнімнің бір түрі үшін қолданылады;
жоспарланған уақыт кезеңінде сұраныс деңгейі тұрақты, яғни біз X
тобының өнімімен айналысамыз;
жеткізілім арасындағы уақыт аралығы тұрақты, ал жеткізу уақыты
тұрақты. Жеткізудің ықтимал кешігуі де болжамды және шектеулі;
әр тапсырыс бір партия түрінде жеткізіледі (яғни, партия бірден, оны
кішігірім бөліктерге бөлмей, бірден келеді және бірден және толықтай
қабылданады). Әр тапсырыс бөлек жеткізілімде болады;
тапсырыс беру құны тұрақты болып табылады. Сатып алу бағасы
тұрақты;
қорды сақтау құны оның мөлшеріне пропорционалды (яғни біз қымбат
тастармен немесе диаметрі екі метрлік шойын құбырларымен
айналыспаймыз);
қойманың өндірістік қуатында шектеулер жоқ (қойма оңтайлы
тапсырысты қабылдай алады);
тапшылықтан шығындар жоқ;
жеткізушімен сіз партияның оңтайлы мөлшері туралы келісе аласыз.
Осындай шектеулерге қарамастан, көптеген компанияларда осы
модельге сәйкес келетін өнімдер жеткілікті. Егер сіздің дүкенде тек
маусымдық немесе коллекциялық өнім болса (мех салоны немесе аяқ киім
бутигі немесе зергерлік бутик), егер тауарлардың көпшілігінде тұрақсыз
сұраныс болса, онда бұл модельді қолданудың қажеті жоқ.
Егер біз үнемі сатылатын тұтыну тауарларымен (тамақ, тұрмыстық
химия, тұрмыстық техника, киім-кешек пен аяқ киім, тұрмыстық заттар,

15.

тоқыма бұйымдары, ыдыс-аяқтар және т.б.) айналысатын болсақ, онда бұл
модель керемет жұмыс істейді.
Оның мәні мынада: тек бір сәтте сатып алу шығындары мен шығындар
минималды. Аз қаражат жұмсау үшін сізге осы нүктені (Qw) табу керек.
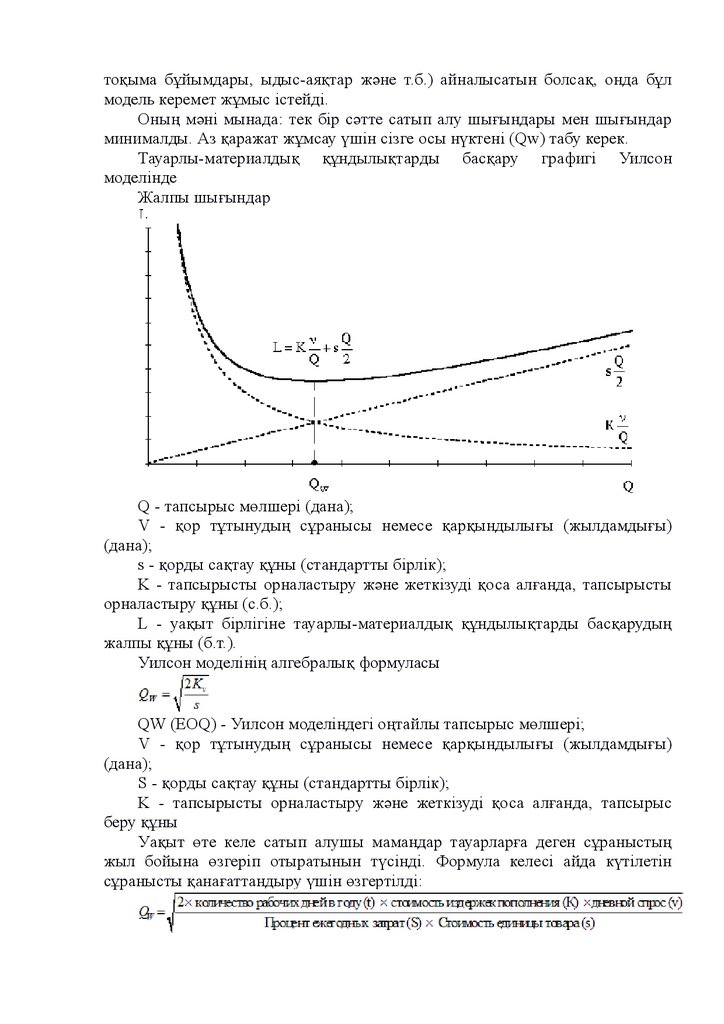
Тауарлы-материалдық құндылықтарды басқару графигі Уилсон
моделінде
Жалпы шығындар
Q - тапсырыс мөлшері (дана);
V - қор тұтынудың сұранысы немесе қарқындылығы (жылдамдығы)
(дана);
s - қорды сақтау құны (стандартты бірлік);
K - тапсырысты орналастыру және жеткізуді қоса алғанда, тапсырысты
орналастыру құны (с.б.);
L - уақыт бірлігіне тауарлы-материалдық құндылықтарды басқарудың
жалпы құны (б.т.).
Уилсон моделінің алгебралық формуласы
QW (EOQ) - Уилсон моделіндегі оңтайлы тапсырыс мөлшері;
V - қор тұтынудың сұранысы немесе қарқындылығы (жылдамдығы)
(дана);
S - қорды сақтау құны (стандартты бірлік);
K - тапсырысты орналастыру және жеткізуді қоса алғанда, тапсырыс
беру құны
Уақыт өте келе сатып алушы мамандар тауарларға деген сұраныстың
жыл бойына өзгеріп отыратынын түсінді. Формула келесі айда күтілетін
сұранысты қанағаттандыру үшін өзгертілді:

16.

Бір тоңазытқышқа тапсырыс беру үшін қанша оңтайлы, егер біз бұрын
есептесек:
Жұмыс күндерінің саны = 360 күн
Толтыру құны = 7 доллар
Сұраныс = күніне 2 тоңазытқыш
Сақтау құны = 16%
Бірлік құны = 200 доллар.
EOZ = v2 * 360 * 7 x 2/0, 16 * 200 = 17, 7 дана. (18 дана.)
МЫСАЛ. Excel кестесіндегі әр түрлі өнімдер үшін EOI есептеу
параметрлері. Есептеуді жеңілдету үшін Вильсон формуласын екі ұяшыққа
бөліңіз.
Кестеден көріп отырғанымыздай, шұжыққа тапсырыс берудің оңтайлы
мәні110 кг... Сонымен қатар, сіз үнемі сатылымда болатын және бағасы төмен
арзан пакетпен мысал қарастыра аласыз. Үлкен партияны (шамамен 2000
дана) алып келу оңтайлы, өйткені пакеттің өзіндік құны төмен, ал тапсырыс
шығындары (менеджердің күш-жігері, тасымалдау және т.б.) пакеттің өзіндік
құнына қатысты жоғары.