Похожие презентации:
Свойства параллельных плоскостей
1.
Геометрия 10 классРешение задач
по теме:
«Свойства параллельных
плоскостей»
Волобуева Елена Викторовна
учитель математики
МАОУ « Андреевская СОШ»
с. Андреевка
Курманаевского района
2.
«Если вы хотите научитьсяплавать, то смело входите в воду,
а если хотите научиться решать
задачи, то решайте их.»
Д.Пойа
3.
Урок решения задач по теме:«Свойства параллельных плоскостей»
Цели урока:
• повторить определение и признак
параллельности плоскостей в пространстве,
• повторить свойства параллельных
плоскостей;
• отработать навыки решения задач по теме
«Свойства параллельных плоскостей».
4.
Продолжи формулировки1. Две плоскости называются параллельными,
если …
2. Если две пересекающиеся прямые одной
плоскости соответственно параллельны…
3. Если две параллельные плоскости пересечены
третьей, то линии их пересечения …
4. Отрезки параллельных прямых, заключенные
между параллельными плоскостями …
5.
Bβ
1. Д а н о : Δ АВС, АС α, АМ = МВ,
М β, β || α, β ВС = K.
Доказать, что МK – средняя линия
Δ АВС.
K
M
C
αA
B
β
2. Одна из сторон треугольника принадлежит
плоскости α. Плоскость β параллельна плоскости
α и пересекает две другие стороны треугольника.
Доказать, что β отсекает от треугольника
треугольник, подобный данному.
K
M
C
αA
D
M
A
K
N
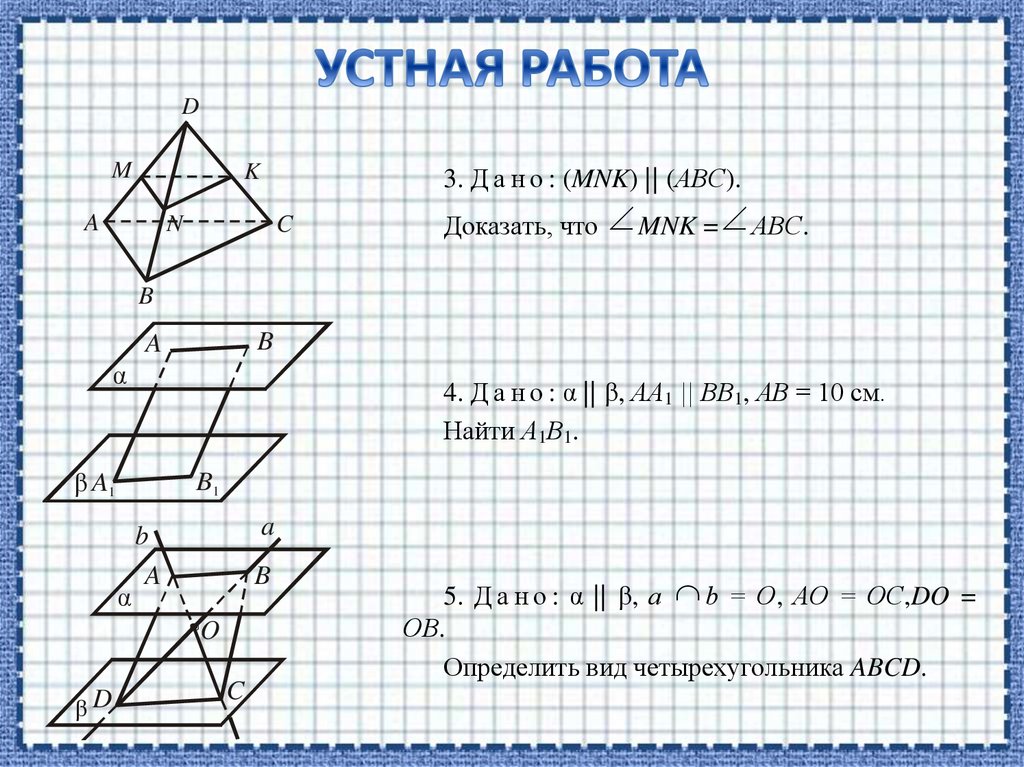
3. Д а н о : (MNK) || (АВС).
C
Доказать, что MNK = АВС.
6.
Доказать, что β отсекает от треугольникатреугольник, подобный данному.
C
αA
D
M
K
A
3. Д а н о : (MNK) || (АВС).
N
C
Доказать, что MNK = АВС.
B
B
A
α
4. Д а н о : α || β, АА1 || ВВ1, АВ = 10 см.
Найти А1В1.
β A1
B1
α
a
b
A
B
O
βD
C
5. Д а н о : α || β, а b = О, АО = ОС,DO =
ОВ.
Определить вид четырехугольника ABCD.
7.
1. Плоскость α параллельна прямой в, а прямая в параллельна плоскости .Взаимное расположение плоскостей α и .
а) параллельны
б) пересекаются
в) совпадают
2. Плоскость пересекает плоскости α и β по параллельным прямым а и в.
Взаимное расположение плоскостей α и β.
а) параллельны
б) пересекаются
в) совпадают
3. Каждая из плоскостей α и β параллельна плоскости . Взаимное расположение
плоскостей α и β.
а) параллельны
б) пересекаются
в) совпадают
4. Каждая из плоскостей α и β параллельна прямой а. Взаимное расположение
плоскостей α и β.
а) параллельны
б) пересекаются
в) совпадают
8.
1. Плоскость α параллельна прямой в, а прямая в параллельна плоскости .Взаимное расположение плоскостей α и .
а) параллельны +
б) пересекаются
в) совпадают +
2. Плоскость пересекает плоскости α и β по параллельным прямым а и в.
Взаимное расположение плоскостей α и β.
а) параллельны +
б) пересекаются
в) совпадают
3. Каждая из плоскостей α и β параллельна плоскости . Взаимное расположение
плоскостей α и β.
а) параллельны +
б) пересекаются
в) совпадают
4. Каждая из плоскостей α и β параллельна прямой а. Взаимное расположение
плоскостей α и β.
а) параллельны +
б) пересекаются
в) совпадают +
9.
Отвечаем на вопросы1. Могут ли прямая и плоскость не иметь общих точек?
2. Верно ли, что если две прямые не пересекаются, то они
параллельны?
3. Плоскости и β параллельны, прямая m не лежит в плоскости .
Верно ли, что прямая m параллельна плоскости β?
4. Верно ли, что если прямая а параллельна одной из двух
параллельных плоскостей, с другой плоскостью прямая а имеет
одну общую точку?
5. Боковые стороны трапеции параллельны плоскости . Верно ли,
что плоскость трапеции параллельна плоскости ?
6. Две стороны трапеции лежат в параллельных плоскостях. Могут
ли эти стороны быть боковыми сторонами трапеции?
7. Верно ли, что плоскости параллельны, если прямая, лежащая в
одной плоскости, параллельна другой плоскости?
8. Верно ли, что линия пересечения двух плоскостей параллельна
одной из этих плоскостей?
9. Верно ли, что любые четыре точки лежат в одной плоскости?
10.Верно ли, что если две стороны треугольника параллельны
плоскости , то и третья сторона параллельна плоскости ?
10.
Проверь свою работу1. Могут ли прямая и плоскость не иметь общих точек? ДА
2. Верно ли, что если две прямые не пересекаются, то они
параллельны? НЕТ
3. Плоскости и β параллельны, прямая m не лежит в плоскости .
Верно ли, что прямая m параллельна плоскости β? ДА
4. Верно ли, что если прямая а параллельна одной из двух
параллельных плоскостей, с другой плоскостью прямая а имеет
одну общую точку? НЕТ
5. Боковые стороны трапеции параллельны плоскости . Верно ли, что
плоскость трапеции параллельна плоскости ? ДА
6. Две стороны трапеции лежат в параллельных плоскостях. Могут ли
эти стороны быть боковыми сторонами трапеции? НЕТ
7. Верно ли, что плоскости параллельны, если прямая, лежащая в
одной плоскости, параллельна другой плоскости? НЕТ
8. Верно ли, что линия пересечения двух плоскостей параллельна
одной из этих плоскостей? НЕТ
9. Верно ли, что любые четыре точки лежат в одной плоскости? НЕТ
10.Верно ли, что если две стороны треугольника параллельны
плоскости , то и третья сторона параллельна плоскости ? ДА
11.
12.
- Какие темы из раздела «Параллельность плоскостей впространстве» использовались при решении задач?
- Какие основные понятия и теоремы применяли?
- Чему научились на уроке?
- Что нового узнали?
Лист учёта знаний учащегося 10 класса
Задание 1
Тест
Задание 2
Отвечаем на
вопросы
Задание 3
Решение задачи
Общее
количество
баллов
13.
Мне всё понятноВопросов нет.
Мне ничего
не понятно.
У меня есть
вопросы.
14.
• п. 10,11 повторить• домашняя контрольная работа
15.
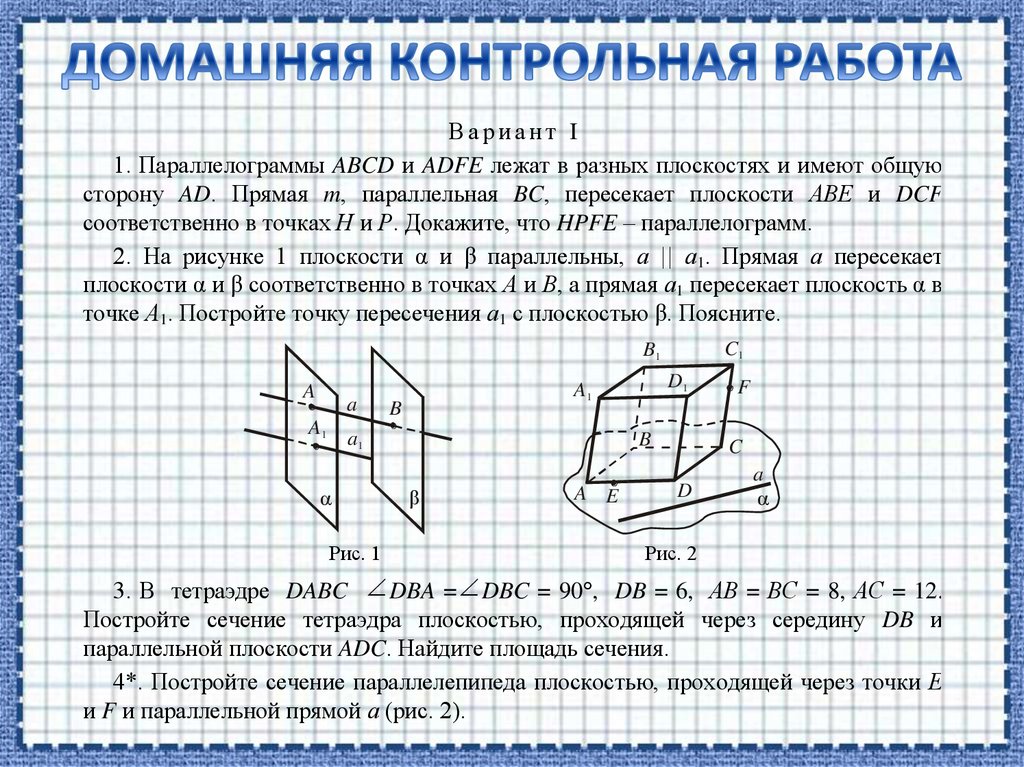
Вариант I1. Параллелограммы ABCD и ADFE лежат в разных плоскостях и имеют общую
сторону AD. Прямая m, параллельная BC, пересекает плоскости АВЕ и DCF
соответственно в точках Н и Р. Докажите, что HPFE – параллелограмм.
2. На рисунке 1 плоскости α и β параллельны, а || а1. Прямая а пересекает
плоскости α и β соответственно в точках А и В, а прямая а1 пересекает плоскость α в
точке А1. Постройте точку пересечения а1 с плоскостью β. Поясните.
C1
B1
A
a
A1
B
a1
α
Рис. 1
D1
A1
B
β
A E
F
C
D
a
α
Рис. 2
3. В тетраэдре DABC DBA = DBC = 90 , DB = 6, АВ = ВС = 8, АС = 12.
Постройте сечение тетраэдра плоскостью, проходящей через середину DB и
параллельной плоскости ADC. Найдите площадь сечения.
4*. Постройте сечение параллелепипеда плоскостью, проходящей через точки Е
и F и параллельной прямой а (рис. 2).
16.
В а р и а н т II1. Вне плоскости α расположен треугольник АВС, у которого медианы АА1 и ВВ1
параллельны плоскости α. Через вершины В и С треугольника проведены
параллельные прямые, которые пересекают плоскость α соответственно в точках Е
и F. Докажите, что ECBF – параллелограмм.
2. На рисунке 1 плоскости α и β параллельны. Прямая а пересекает плоскости α и
β соответственно в точках А и В, а прямая b – в точках С и D. Найдите взаимное
положение прямых а и b. Поясните.
a
A
B
b
M
Cα
D β
Рис. 1
K
B
A
C
α
a
Рис. 2
3. Все грани параллелепипеда ABCDA1B1C1D1 – квадраты со стороной а. Через
середину AD параллельно плоскости DA1B1 проведена плоскость. Найдите периметр
сечения.
4*. Постройте сечение тетраэдра плоскостью, проходящей через точки С и К и
параллельной прямой а (рис. 2).
17.
В а р и а н т III1. Прямоугольники ABCD и EBCF лежат в разных плоскостях и имеют общую
сторону ВС. Прямая а параллельна AD и пересекает плоскости АВЕ и DCF
соответственно в точках Р и Н. Докажите, что РВСН – параллелограмм.
2. На рисунке 1 плоскости α и β параллельны. Прямые а и b пересекаются в точке
М. Прямая а пересекает плоскости α и β соответственно в точках А и В, а прямая b
пересекает плоскость β в точке D. Постройте точку пересечения прямой b с
плоскостью α.
B1
α
A
a
B
D1
A1
M
b
D
Рис. 1
E
A
β
C1
B
P
C
D
a
α
Рис. 2
3. В тетраэдре DABC точка М – середина АС, DB = 6, MD = 10,
DBM = 90°. Постройте сечение тетраэдра плоскостью, проходящей через
середину ребра DC и параллельной плоскости DMB, и найдите площадь сечения.
4*. Постройте сечение параллелепипеда плоскостью, проходящей через точки Е
и Р и параллельной прямой а (рис. 2).
18.
В а р и а н т IV1. Трапеция ABCD (AD и ВС – основания) расположена вне плоскости α.
Диагонали трапеции параллельны плоскости α. Через вершины А и В проведены
параллельные прямые, которые пересекают плоскость α в точках Е и F
соответственно. Докажите, что EABF – параллелограмм.
2. На рисунке 1 плоскости α и β параллельны. Прямая а пересекает плоскости α и
β соответственно в точках А и В, а прямая b – в точках С и D. Каково взаимное
положение прямых а и b? Поясните.
a
A
α
β
D
D
b
C
M
B
α
B
A
a
C
Рис. 1
Рис. 2
3. Дан параллелепипед ABCDA1B1C1D1, все грани которого – прямоугольники,
AD = 4, DC = 8, СС1 = 6. Постройте сечение параллелепипеда плоскостью,
проходящей через середину ребра DC и параллельной плоскости AB1C1, и найдите
периметр сечения.
4*. Постройте сечение тетраэдра плоскостью, проходящей через точки С и М и
параллельной прямой а (рис. 2).

















 Математика
Математика