Умножение одночленов. Возведение одночленов в натуральную степень

1. Умножение одночленов. Возведение одночленов в натуральную степень.

2.

1.
2.
3.
4.
Алгебраическое выражение, которое представляет
собой произведение чисел и переменных, возведенных в
степени с натуральными показателями называют
одночленом.
Числовой множитель одночлена, записанного в
стандартном виде, называют коэффициентом одночлена
Одинаковые или отличающиеся только
коэффициентами одночлены называют подобными
Одночлен, в котором единственный числовой
множитель стоит на первом месте и степень любой
переменной входит множителем только один раз,
называют одночленом стандартного вида

3.

6. Как умножить один одночлен на другой?
Чтобы умножить одночлен на одночлен нужно :
- перемножить числовые множители этих одночленов;
- перемножить степени с одинаковыми основаниями.
7. Каким правилом пользуются при возведении одночлена в
натуральную степень?
Чтобы возвести в степень произведение нескольких множителей
нужно в эту степень возвести каждый множитель.

4.

10х3 и -2х3
Сумма
Разность
Произведение
Квадрат первого
Квадрат второго
Квадрат их суммы
Квадрат их разности
Сумма их квадратов
Разность их квадратов
Куб первого одночлена
Куб второго одночлена
Произведение этих одночленов
и одночлена (-5ху)
8х3
12х3
-20х6
100х6
4х6
64х6
144х6
104х6
96х6
1000х9
-8х9
100х7у

5. Запишите выражение в вида квадрата или куба

1000x12y6=
-125c3y9=
1000x12y6=(10x4y2)3 -125c3y9= (-5cy3)3
64a6b12=
64a6b12= (8a3b6)2
25х2=
25х2= (5x)2
-100x12y2=
27a6b12=
100x12y2=(10x6y)2 27a6b12= (3a2b4)3

6.

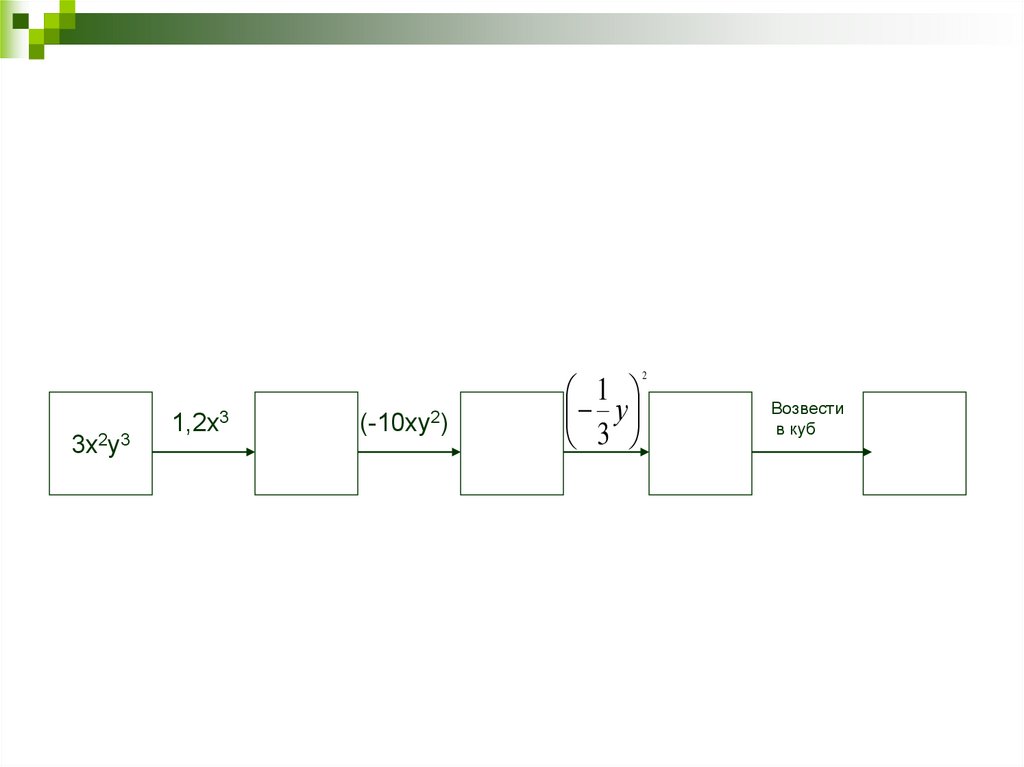
3х2у3
1,2х3
(-10ху2)
1
у
3
2
Возвести
в куб

7. Верно ли равенство?

3
3
2х
2х6
3
9
( a 2 b 3c ) 2 a 4 b 5 c
4
4
3
2
5 3 85
3 13
1 3
5
ху 4 у
2 х у
32 х у
2

8.

1. Выполнить умножение
1
0,5a 2b3 4 ab 2
2
2ab 0,3a b
3a b 0,1ab
5a b 0,1ab
3
3
2
2
3
3
8ab 0,5ab
2a b 0,1ab
2
2
3
2. Возвести в степень
2
0,2a b в куб
0,3a b в квадрат
9
a b в квадрат
4
4a b в квадрат
0,6a b в квадрат
4
3
2
3
3
5
4
4
3
4
5
3
0,5a b в квадрат
3. Выполнить умножение
16a 4 b 6 (ab 3 )
0,008a 12b 9 10ab
2
2
1
0,09a 6 b 8 3 a
3
3
81 6 10
a b 2a 2 b
16
0,25a 8 b 6 10ab 2
1
0,36a b a
6
8
2
10
4. Вычислить значение выражения
7
8
a b при а=-1, b=-1
0,01a b при a=-1, b=-1
0,8a b при a=-1, b=-1
10
14
11
2,5a 9b8 при a=-1, b=-1
10
5
16a b
9
при a=-1, b=-1
81
a b при a=-1, b=-1
2
12
13