Математический диктант

1.

1.
2.
3.
4.
5.
6.
Вариант 1
Как называется раздел
геометрии, изучающий
фигуры в пространстве?
Назовите основные фигуры
в пространстве.
Сформулируйте аксиому
А2.
Сформулируйте аксиому
А3.
Могут ли прямая и
плоскость иметь только две
общие точки?
Сколько плоскостей можно
провести через три точки?
1.
2.
3.
4.
5.
6.
Вариант 2
Как называется раздел
геометрии, изучающий
фигуры на плоскости?
Назовите основные фигуры
на плоскости.
Сформулируйте аксиому
А1.
Сколько плоскостей можно
провести через прямую и
не лежащую на ней точку?
Сколько может быть общих
точек у прямой и
плоскости?
Могут ли прямая и
плоскость иметь одну
общую точку?

2.

3.

Определение параллельных прямых.
Взаимное расположение 2-х прямых на
плоскости.
Сколько можно провести параллельных
прямых через точку А к прямой а. Почему?
Аксиома параллельных.

4.

Определение: Две прямые в пространстве
называются параллельными, если они лежат
в одной плоскости и не пересекаются.

5.

Дано: а, М
а
Провести через М прямую
bǁа.
Доказать, что b !
Доказательство
1. (а,M) α, по теореме 1
2. Проведем bǁ а
3. По аксиоме планиметрии известно, что
через точку М вне прямой а можно провести
прямую, параллельную данной и притом
только одну.

6.

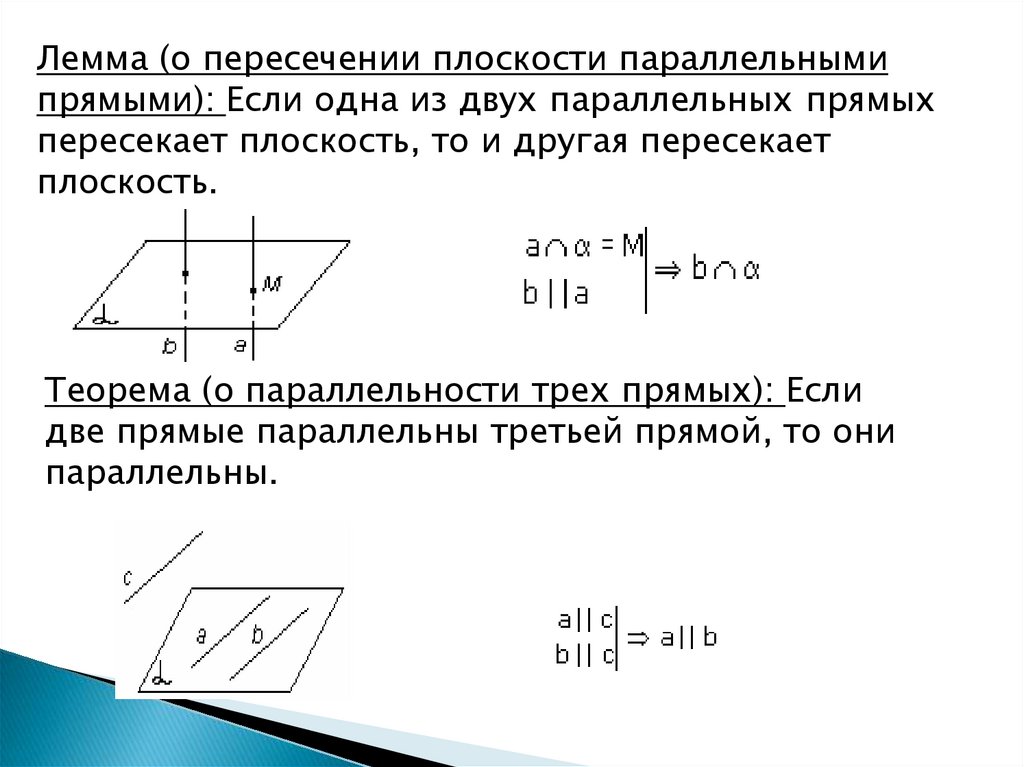
Лемма (о пересечении плоскости параллельными
прямыми): Если одна из двух параллельных прямых
пересекает плоскость, то и другая пересекает
плоскость.
Теорема (о параллельности трех прямых): Если
две прямые параллельны третьей прямой, то они
параллельны.

7.

Случаи взаимного расположения прямой и плоскости:
а) прямая лежит в плоскости;
б) прямая и плоскость имеют только одну общую
точку;
в) прямая и плоскость не имеют ни одной общей
точки.
Определение: Прямая и плоскость называются
параллельными, если они не имеют общих точек .

8.

Дано: а, b, α
а α, b α, аǁ b
Доказать, что аǁα
Доказательство
Пусть а α b α, по лемме о пересечении
плоскости параллельными прямыми.
Но b α а α, а значит аǁα

9.

1.
2.
Отрезок АВ не пересекает плоскость α. Через
середину отрезка С и концы отрезка А и В
проведены прямые, параллельные между собой и
пересекающие плоскость α в точках А1, В1, С1.
Вычислить длину отрезка СС1, если АА1=5,
ВВ1=7.
Точка М лежит на отрезке АВ. Отрезок АВ
пересекает плоскость α в точке В. Через А и М
проведены параллельные прямые, пересекающие
α в точках А1и М1. Найдите длину отрезка АВ,
если АА1: ММ1=3:2, АМ=6.

10.

§1 п. 4,5,6 стр. 9-13