Решение задач на применение аксиом стереометрии и их следствий. Урок 1

1.

Урок 1.
Добрый день!
Начинаем нашу работу
14.09.2023
Классная работа
Решение задач на
применение аксиом
стереометрии и их следствий.

2.

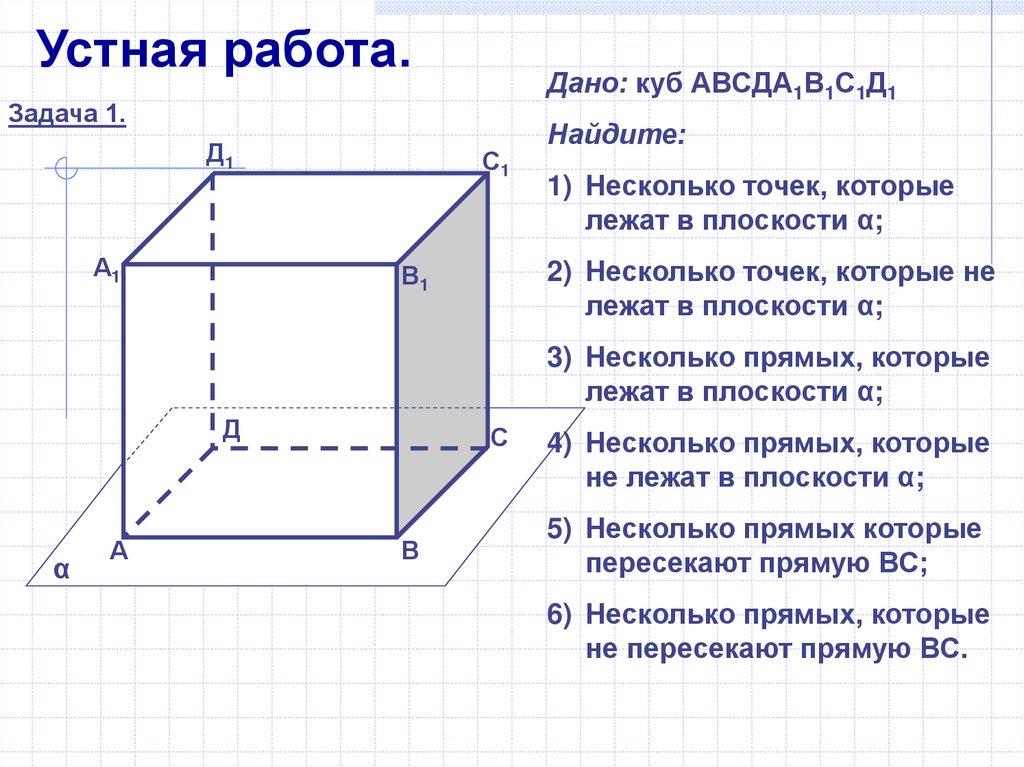
Устная работа.
Дано: куб АВСДА1В1С1Д1
Задача 1.
Д1
А1
С1
Найдите:
1) Несколько точек, которые
лежат в плоскости α;
2) Несколько точек, которые не
лежат в плоскости α;
В1
3) Несколько прямых, которые
лежат в плоскости α;
Д
α
А
С
В
4) Несколько прямых, которые
не лежат в плоскости α;
5) Несколько прямых которые
пересекают прямую ВС;
6) Несколько прямых, которые
не пересекают прямую ВС.

3.

Устная работа.
b
Задача 2.
А
М
а
α
В
c
Заполните пропуски, чтобы получилось верное утверждение:
1)еслиА а, а , тоА.....
2)еслиА , В , тоАВ.....
3)еслиА ; В ; С АВ, тоС...
4)еслиМ ; М , а, тоМ ....а

4.

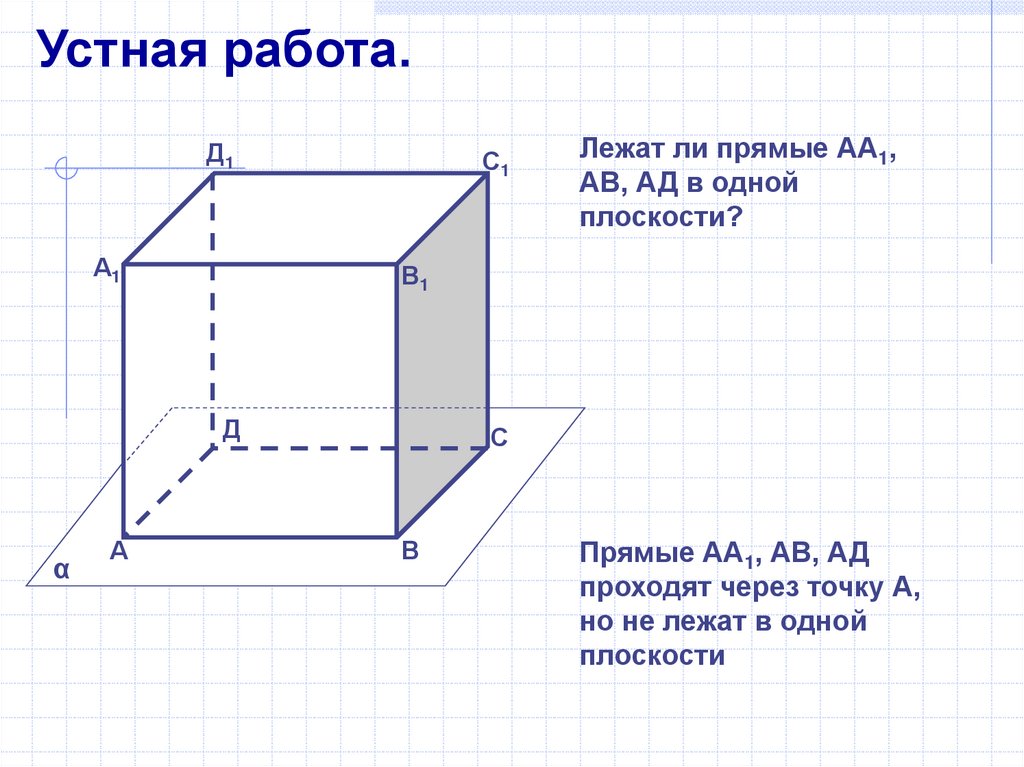
Устная работа.
Д1
А1
С1
В1
Д
α
А
Лежат ли прямые АА1,
АВ, АД в одной
плоскости?
С
В
Прямые АА1, АВ, АД
проходят через точку А,
но не лежат в одной
плоскости

5.

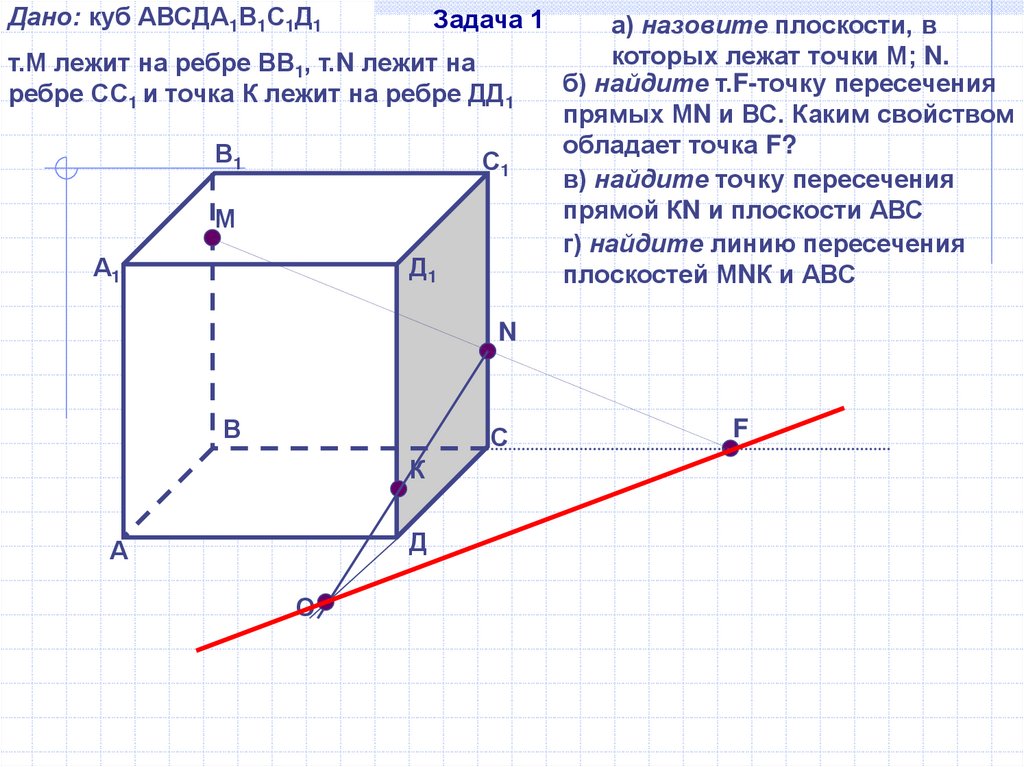
Дано: куб АВСДА1В1С1Д1
Задача 1
т.М лежит на ребре ВВ1, т.N лежит на
ребре СС1 и точка К лежит на ребре ДД1
В1
С1
М
А1
Д1
а) назовите плоскости, в
которых лежат точки М; N.
б) найдите т.F-точку пересечения
прямых МN и ВС. Каким свойством
обладает точка F?
в) найдите точку пересечения
прямой КN и плоскости АВС
г) найдите линию пересечения
плоскостей МNК и АВС
N
В
С
К
Д
А
О
F

6.

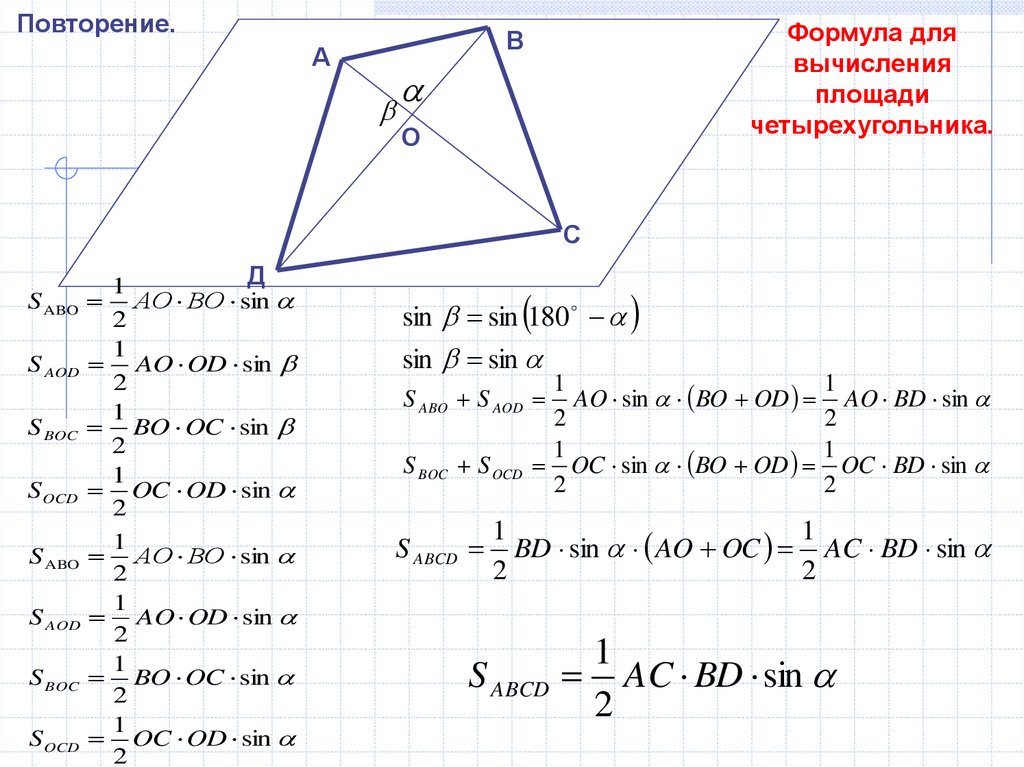
Повторение.
Формула для
вычисления
площади
четырехугольника.
В
А
О
С
Д
1
S ABO АО ВО sin
2
1
S AOD AO OD sin
2
1
S BOC BO OC sin
2
1
S OCD OC OD sin
2
1
S ABO АО ВО sin
2
1
S AOD AO OD sin
2
1
S BOC BO OC sin
2
1
S OCD OC OD sin
2
sin sin 180
sin sin
1
1
AO sin BO OD AO BD sin
2
2
1
1
S BOC S OCD OC sin BO OD OC BD sin
2
2
S ABO S AOD
S ABCD
1
1
BD sin AO OC AC BD sin
2
2
1
S ABCD AC BD sin
2

7.

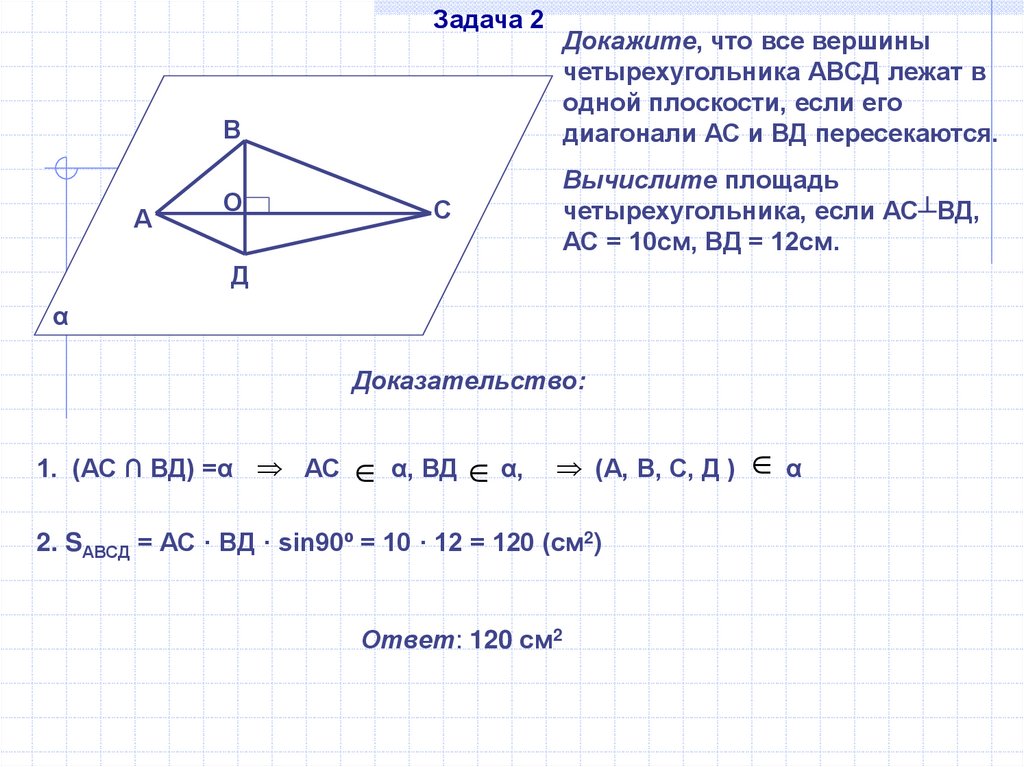
Задача 2
Докажите, что все вершины
четырехугольника АВСД лежат в
одной плоскости, если его
диагонали АС и ВД пересекаются.
В
А
О
Вычислите площадь
четырехугольника, если АС┴ВД,
АС = 10см, ВД = 12см.
С
Д
α
Доказательство:
1. (АС ∩ ВД) =α АС α, ВД α,
(А, В, С, Д ) α
2. SАВСД = АС · ВД · sin90º = 10 · 12 = 120 (см2)
Ответ: 120 см2

8.

Домашнее задание:
1. Пункты 1-3 прочитать
2. Решить задачи № 10; 13
3. Дополнительно №15 ( по желанию)

9.

Урок 2.
19.09.2023
Классная работа
Решение задач на
применение аксиом
стереометрии и их следствий.

10.

Математический диктант
1 вариант
2 вариант
1. Как называется раздел
геометрии, изучающий
фигуры в пространстве?
1. Как называется раздел
геометрии, изучающий
фигуры на плоскости?
2. Назовите основные фигуры
в пространстве.
2. Назовите основные фигуры
на плоскости.
3. Сформулируйте аксиому А2. 3. Сформулируйте аксиому А1.
4. Сформулируйте аксиому А3. 4. Сколько плоскостей можно
провести через прямую и не
5. Могут ли прямая и
лежащую на ней точку?
плоскость иметь две общие
точки?
5. Сколько может быть точек у
прямой и плоскости?
6. Сколько плоскостей можно
провести через одну точку? 6. Могут ли прямая и
плоскость иметь одну
общую точку?

11.

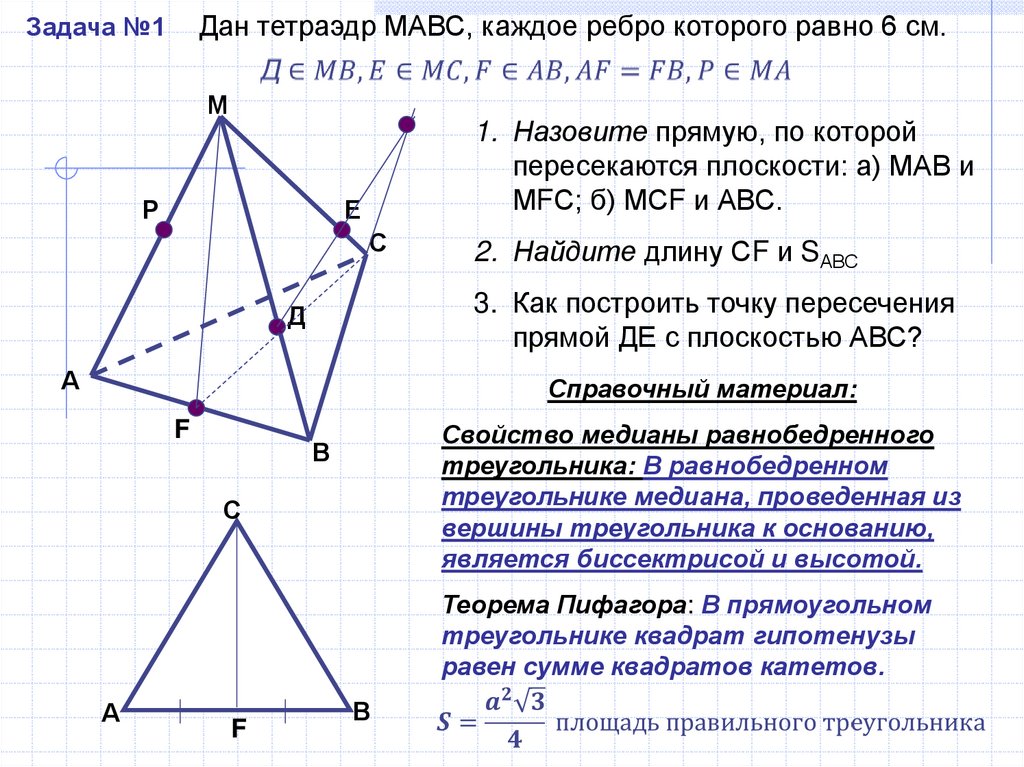
Дан тетраэдр МАВС, каждое ребро которого равно 6 см.
Задача №1
М
Р
1. Назовите прямую, по которой
пересекаются плоскости: а) МАВ и
МFС; б) МСF и АВС.
Е
С
2. Найдите длину СF и SАВС
3. Как построить точку пересечения
прямой ДЕ с плоскостью АВС?
Д
А
Справочный материал:
F
Свойство медианы равнобедренного
треугольника: В равнобедренном
треугольнике медиана, проведенная из
вершины треугольника к основанию,
является биссектрисой и высотой.
В
С
Теорема Пифагора: В прямоугольном
треугольнике квадрат гипотенузы
равен сумме квадратов катетов.
А
F
В

12.

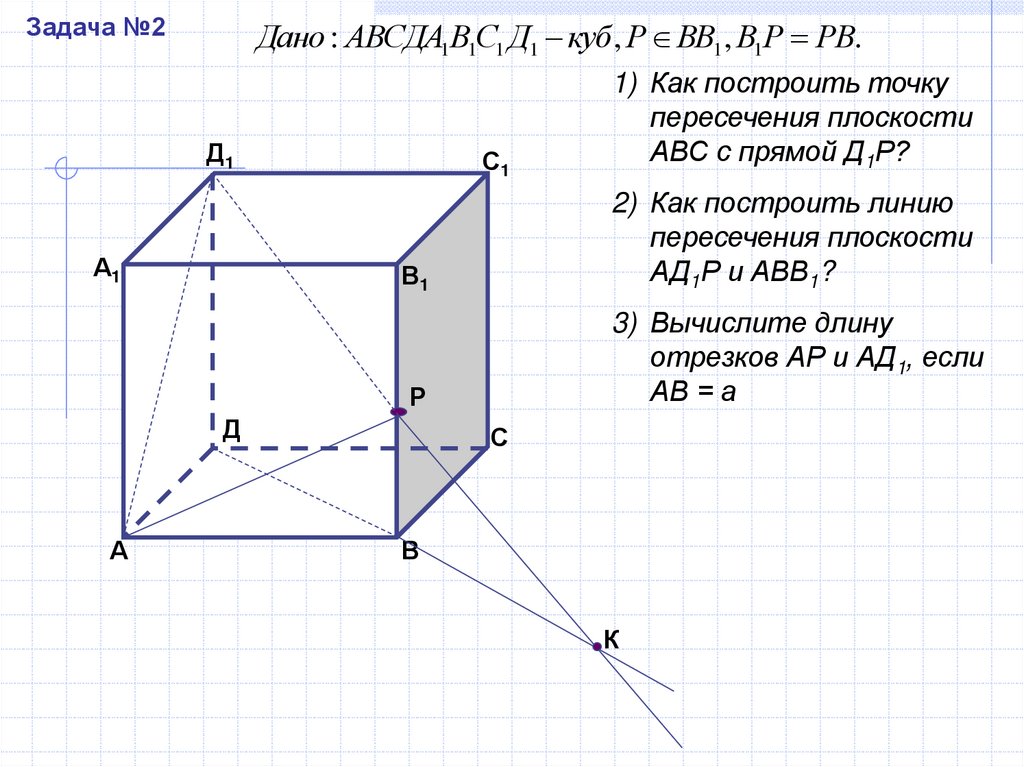
Задача №2
Дано : АВСДА1В1С1 Д1 куб , Р ВВ1, В1Р РВ.
Д1
А1
С1
В1
2) Как построить линию
пересечения плоскости
АД1Р и АВВ1?
Р
3) Вычислите длину
отрезков АР и АД1, если
АВ = а
Д
А
1) Как построить точку
пересечения плоскости
АВС с прямой Д1Р?
С
В
К

13.

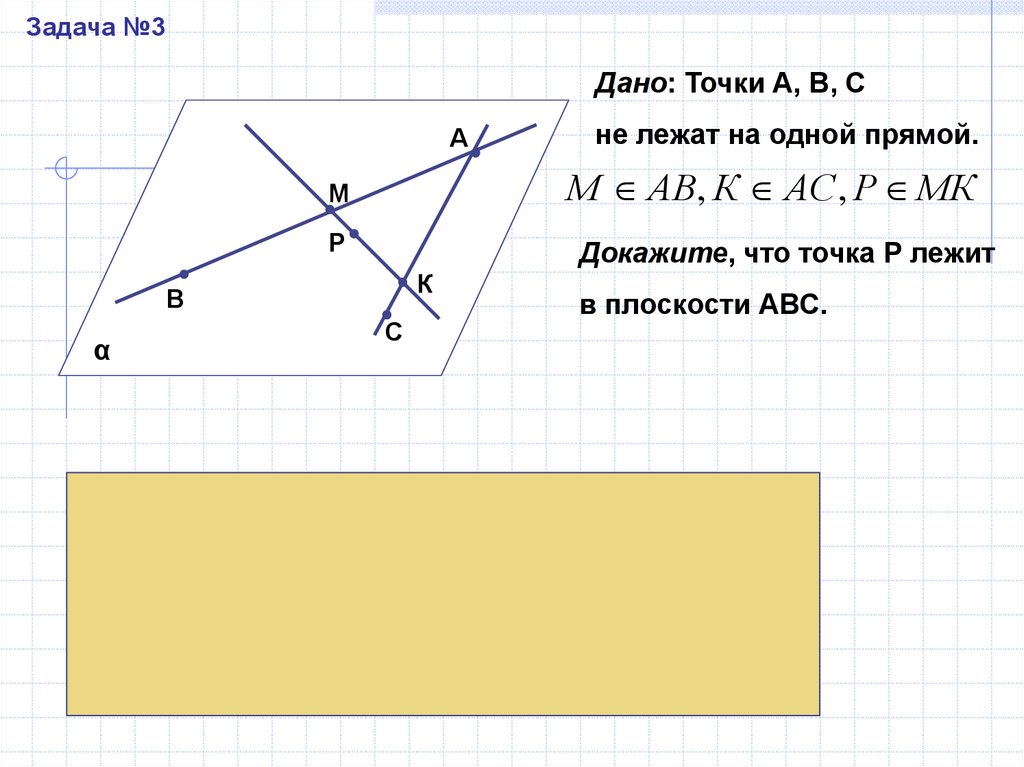
Задача №3
Дано: Точки А, В, С
А
М
М АВ, К АС , Р МК
Р
Докажите, что точка Р лежит
К
В
α
не лежат на одной прямой.
С
в плоскости АВС.
Решение:
АВ ∩ АС = А. По второму следствию (T1), прямые АВ и АС
определяют плоскость α. Точка М ∈ АВ, а значит,
принадлежит плоскости α, и точка К ∈ АС, а значит, и
плоскости α.
По аксиоме А2: МК ⊂ α. Точка Р ∈ МК, а значит, и
плоскости α.

14.

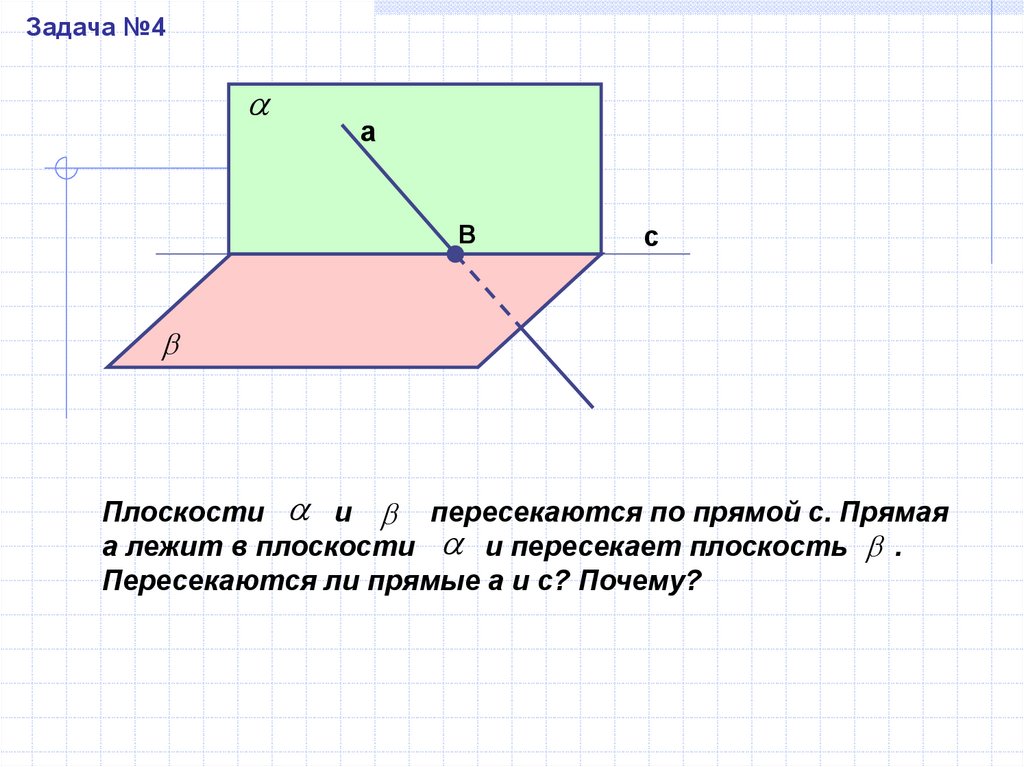
Задача №4
а
В
с
Плоскости и пересекаются по прямой с. Прямая
а лежит в плоскости и пересекает плоскость .
Пересекаются ли прямые а и с? Почему?

15.

Задача №4
а
В
с
Решение:
По условию, прямая а пересекает плоскость β.
Пусть a ∩ β = В (В ∈ а). По условию прямая а
принадлежит плоскости а, значит, В ∈ а. По аксиоме А3
существует прямая с, такая, что B ∈ c.

16.

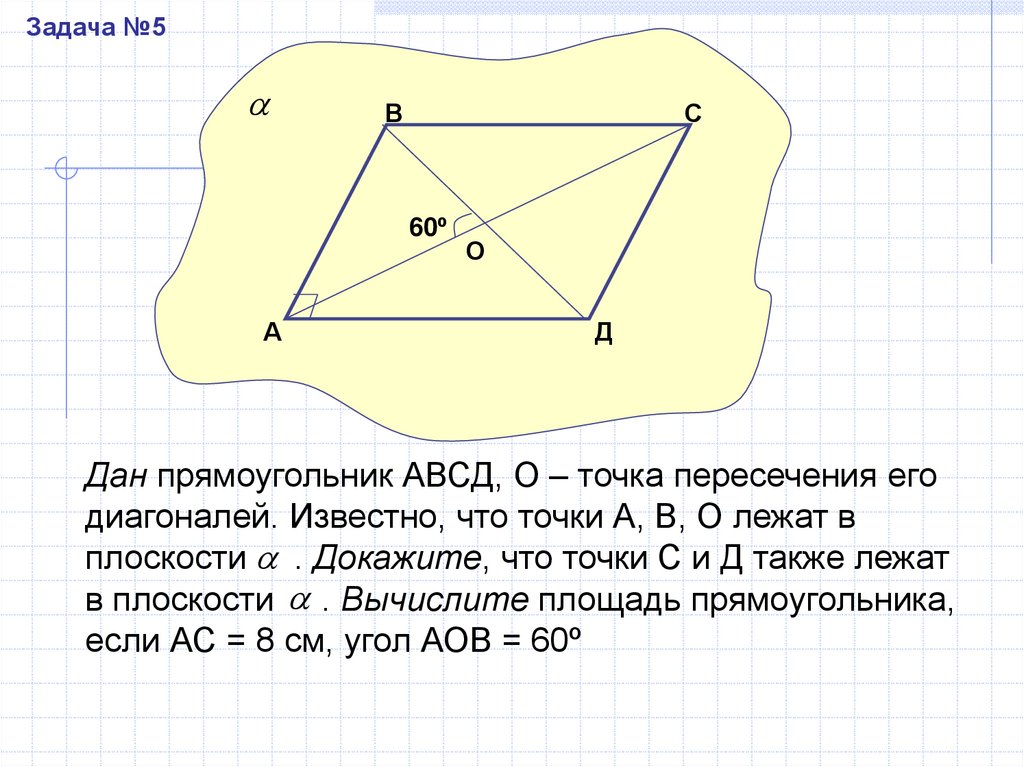
Задача №5
В
С
60º
А
О
Д
Дан прямоугольник АВСД, О – точка пересечения его
диагоналей. Известно, что точки А, В, О лежат в
плоскости . Докажите, что точки С и Д также лежат
в плоскости . Вычислите площадь прямоугольника,
если АС = 8 см, угол АОВ = 60º

17.

Домашнее задание: пункты 1-3 прочитать.
Решить задачи:
1. Прямые а и b пересекаются в точке О, А а, В b,
Р АВ. Докажите, что прямые а и b и точка Р лежат в
одной плоскости.
2. На данном рисунке плоскость содержит точки А, В,
С, Д, но не содержит точку М. Постройте точку К –
точку пересечения прямой АВ и плоскости МСД. Лежит
ли точка К в плоскости .
М
С
А
В
Д