Похожие презентации:
Формулы Ньютона-Котеса
1.
ФОРМУЛЫНЬЮТОНА-КОТЕСА:
МЕТОДЫ ЯМОУГОЛЬНИКОВ, ТРАПЕЦИЙ,
ПАРАБОЛ. ИНТЕГРИРОВАНИЕ С
ПОМОЩЬЮ ФОРМУЛ ГАУССА
2.
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ• Под численным интегрированием
понимается интегрирование
аналитических выражений с
помощью методов приближенных
численных методов, т.е. методов,
сводящихся к выполнению
конечного числа элементарных
операций над числами.
3.
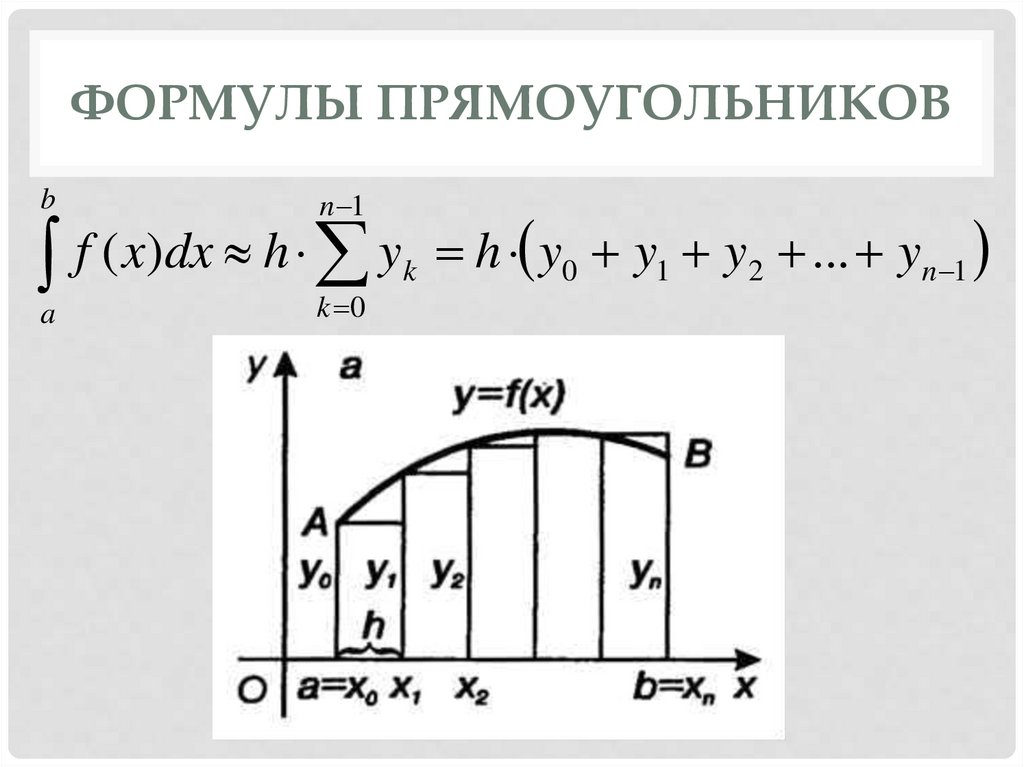
ФОРМУЛЫ ПРЯМОУГОЛЬНИКОВb
n 1
f ( x)dx h y h y y y ... y
a
k 0
k
0
1
2
n 1
4.
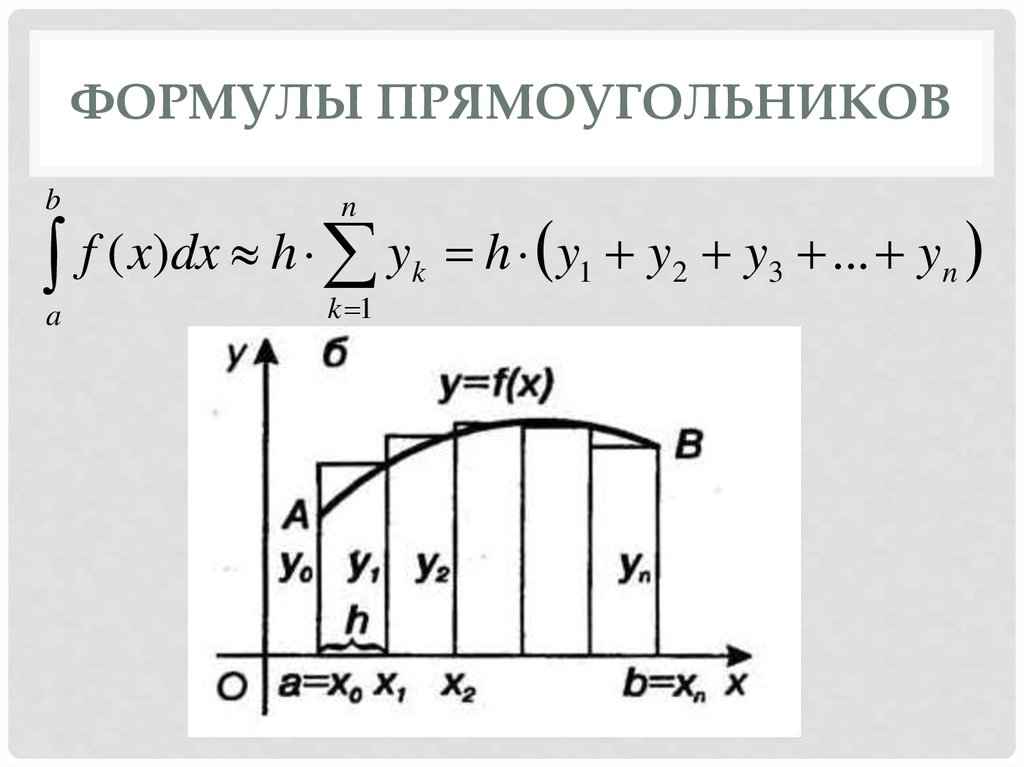
ФОРМУЛЫ ПРЯМОУГОЛЬНИКОВb
n
f ( x)dx h y h y y y ... y
a
k 1
k
1
2
3
n
5.
ПО ФОРМУЛАМ ПРЯМОУГОЛЬНИКОВ,ПРИНЯВ n=4 , ВЫЧИСЛИТЬ
9
dx
1 x 2
6.
,АБСОЛЮТНАЯ ПОГРЕШНОСТЬ МЕТОДА
ПРЯМОУГОЛЬНИКОВ ОПРЕДЕЛЯЕТСЯ
НЕРАВЕНСТВОМ
b a M
2
2 n
M max f ( x)
a x b
7.
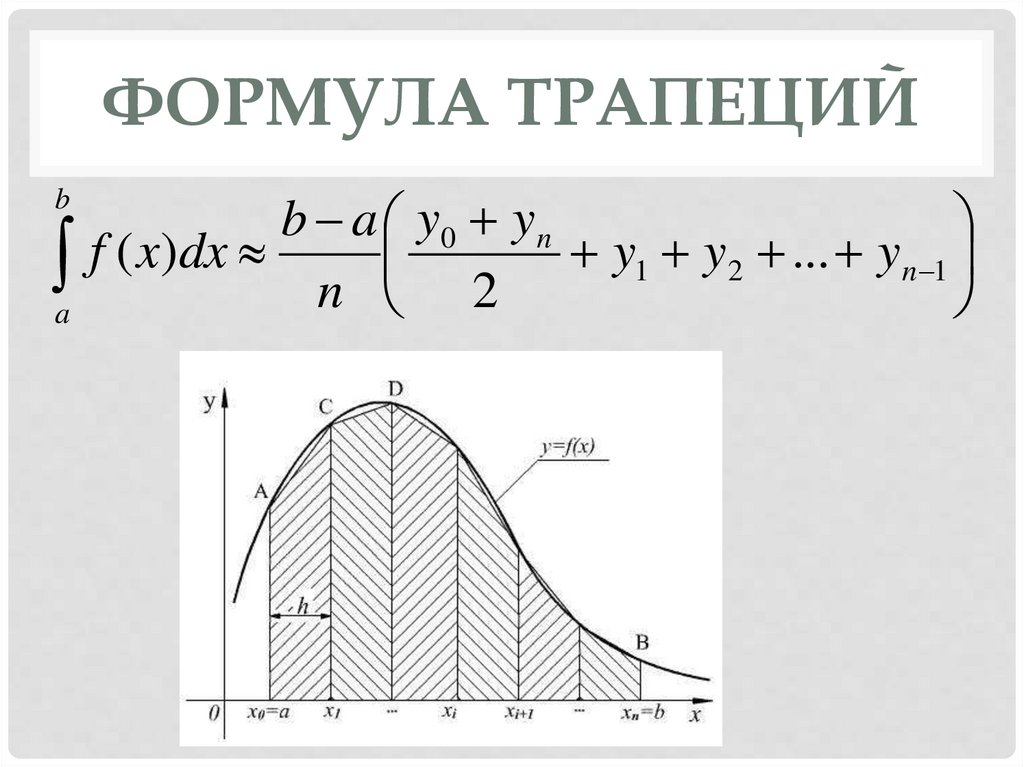
ФОРМУЛА ТРАПЕЦИЙb a y0 y n
a f ( x)dx n 2 y1 y2 ... yn 1
b
8.
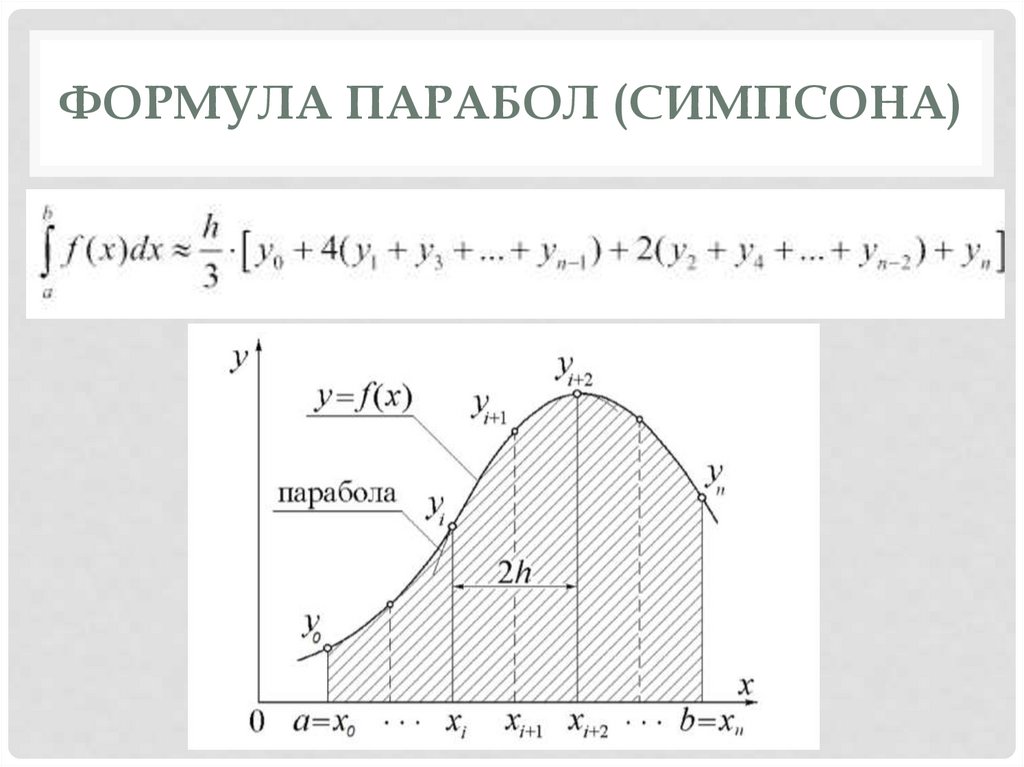
ФОРМУЛА ПАРАБОЛ (СИМПСОНА)9.
ДОМАШНЕЕ ЗАДАНИЕВычислите интеграл:
10
0
dx
x 4
• по формулам прямоугольников
(n=4);
• по формуле трапеций (n=5);
• по формуле Симпсона (2n=10).





 Математика
Математика








