Похожие презентации:
Устойчивость линейных стационарных автоматических систем
1.
Автоматика и управлениеТема 5. Устойчивость линейных
стационарных автоматических
систем
ПЗ 8. Определение устойчивости ЛСС с
использованием частотных критериев.
2.
Задача № 1С помощью критерия Михайлова оценить
характеристическое уравнение которой имеет вид:
устойчивость
АС,
0,0014р4+0,022р3+0,7р2+1,6р+5=0
Решение:
Проверяем выполнение необходимого условия:
I ai 0 (i=0…4)
Согласно критерию Михайлова поворот вектор-функции Михайлова для
устойчивой системы должен быть равен:
Δ =n 4 2
2
2
Подставляем вместо комплексной переменной р, комплексную
переменную j . Полученную таким образом вектор-функцию Михайлова
запишем в виде:
А(j )=0,0014 4-j0,022 3-0,7 2+j1,6 +5
А(j )=Х( )+jY( )
А(j )=(0,0014 4-0,7 2+5)+j(1,6 -0,022 3)
Х( )=5-0,7 2+0,0014 4
Y( )=1,6 -0,022 3
3.
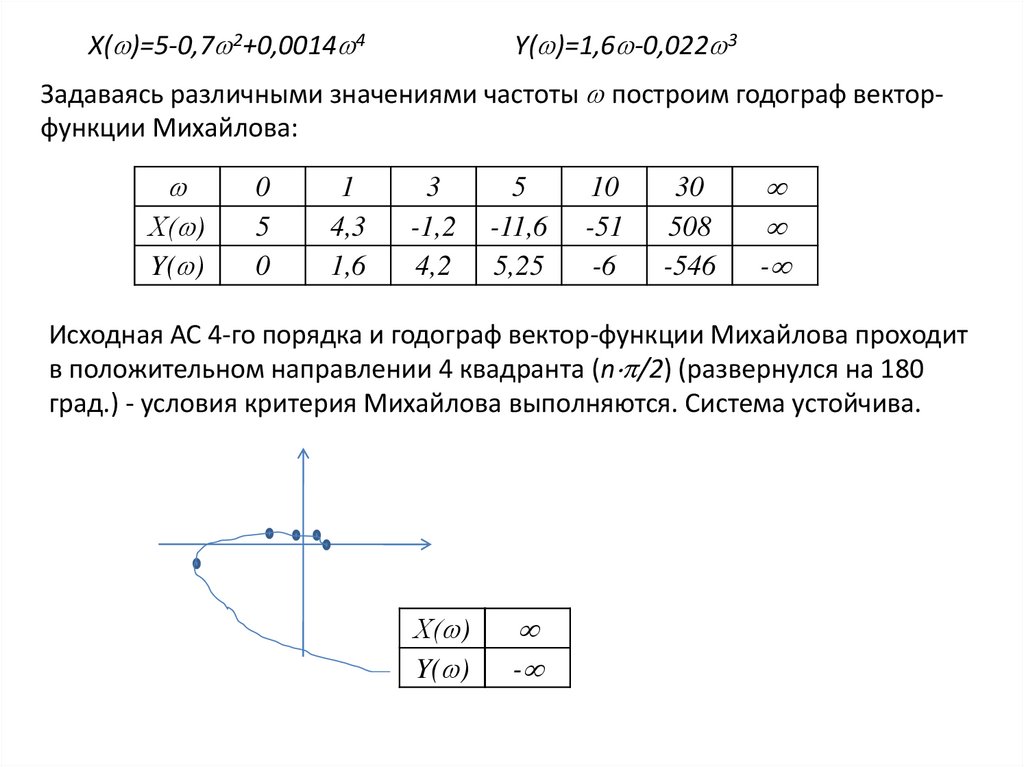
Х( )=5-0,7 2+0,0014 4Y( )=1,6 -0,022 3
Задаваясь различными значениями частоты построим годограф векторфункции Михайлова:
Х( )
Y( )
0
5
0
1
4,3
1,6
3
-1,2
4,2
5
-11,6
5,25
10
-51
-6
30
508
-546
-
Исходная АС 4-го порядка и годограф вектор-функции Михайлова проходит
в положительном направлении 4 квадранта (n /2) (развернулся на 180
град.) - условия критерия Михайлова выполняются. Система устойчива.
Х( )
Y( )
-
4.
Задача №2Определить устойчивость АС с характеристическим уравнением
р5+р4+3р3+2р2+р+0,5=0
Решение:
Функция Михайлова
А(j )=(j )5+(j )4+3(j )3+2(j )2+(j )+0,5= j 5+ 4-j3 3-2 2 +j +0,5=
= 4-2 2+0,5+j( 5-3 3+ )
Определяем корни действительной и мнимой частей А(j )
Действительной части:
4-2 2+0,5=0
в в 2 4 ас
х1,2
2а
2 4 2 2 2
2
2
2
в
в2
х1 , 2
с
2
4
1,7
1 1,7 1,3
0,3
2 0,3 0,55
Из физических соображений 1= -1,3 и 2= -0,55 не учитываем, т.к.
отрицательных частот не существует
5.
Мнимой части:5-3 3+ =0
4-3 2+1=0
3=0
2,6
3 9 4 3 5
2
2
0,4
2
4=1,6; 6=0,63
Располагаем корни в порядке возрастания
3=0, 2=0,55, 5=0,63, 1=1,3; 4=1,6.
R
I
R
I
Корни чередуются – система устойчива
R
6.
Методика оценки устойчивости системы по следствиюкритерия Михайлова:
а) определяем для замкнутой АС функцию Михайлова
А(j )=X( )+jY( ).
б)вычисляем корни вещественной и мнимой
составляющих
Х( )=0; Y( )=0
и располагаем их в порядке возрастания их значений.
в) анализируем порядок следования корней
вещественной и мнимой частей.
Если они чередуются между собой, т.е. вектор-функция
Михайлова последовательно пересекает координатные
оси, - система устойчива. В противном случае –
неустойчива.
7.
Задача №3Определить устойчивость замкнутой АС по критерию Найквиста, если её
передаточная функция в разомкнутом состоянии имеет вид:
W( p )
20( 0 ,1 p 1 )
.
p( 0 ,05 p 1 )
Решение:
Как следует из вида передаточной функции, характеристический полином
разомкнутой АС имеет один нулевой корень ( р=1) и один корень в правой
полуплоскости ( р=1). Разомкнутая система неустойчива.
Строим АФЧХ разомкнутой системы:
20( 0 ,1 j 1 )
3
20(0,1 j 1)( 0,05 2 j )
W ( j )
j ( 0 ,05 j 1 )
2 (0,0025 2 1)
( 0 ,0025 2 1 )
20 0 ,1 2
j
U ( ) jV ( ).
2
( 0 ,0025 1 )
8.
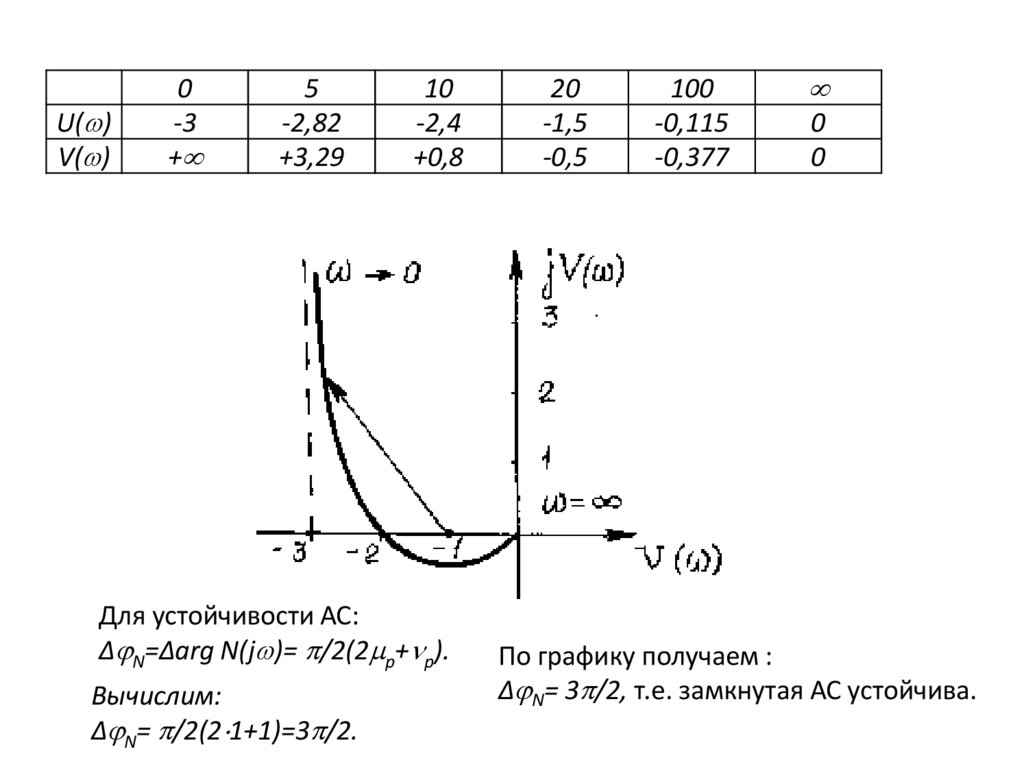
U( )V( )
0
-3
+
5
-2,82
+3,29
10
-2,4
+0,8
Для устойчивости АС:
∆ N=∆arg N(j )= /2(2 р+ р).
Вычислим:
∆ N= /2(2 1+1)=3 /2.
20
-1,5
-0,5
100
-0,115
-0,377
0
0
По графику получаем :
∆ N= 3 /2, т.е. замкнутая АС устойчива.
9.
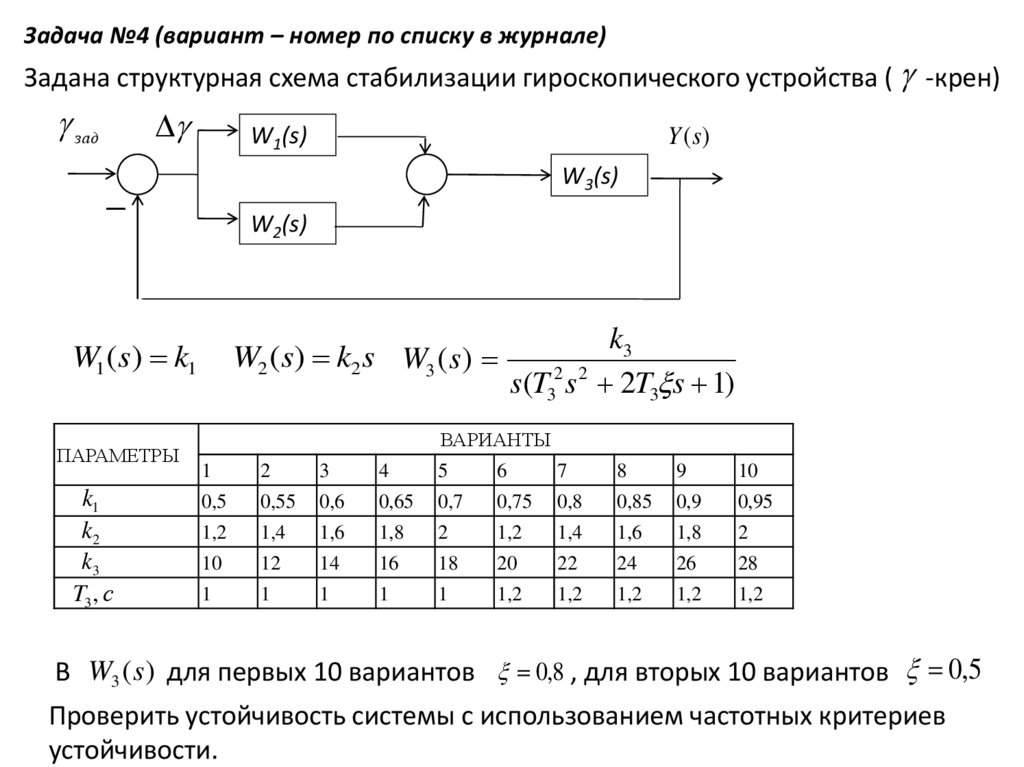
Задача №4 (вариант – номер по списку в журнале)Задана структурная схема стабилизации гироскопического устройства ( -крен)
зад
W1(s)
W3(s)
W2(s)
W1 (s) k1
ПАРАМЕТРЫ
k1
k2
k3
T3 , с
Y (s)
W2 (s) k2 s W3 ( s)
k3
s(T32 s 2 2T3 s 1)
ВАРИАНТЫ
1
2
3
4
5
6
7
8
9
10
0,5
0,55
0,6
0,65
0,7
0,75
0,8
0,85
0,9
0,95
1,2
1,4
1,6
1,8
2
1,2
1,4
1,6
1,8
2
10
12
14
16
18
20
22
24
26
28
1
1
1
1
1
1,2
1,2
1,2
1,2
1,2
В W3 ( s) для первых 10 вариантов 0,8 , для вторых 10 вариантов 0,5
Проверить устойчивость системы с использованием частотных критериев
устойчивости.
10.
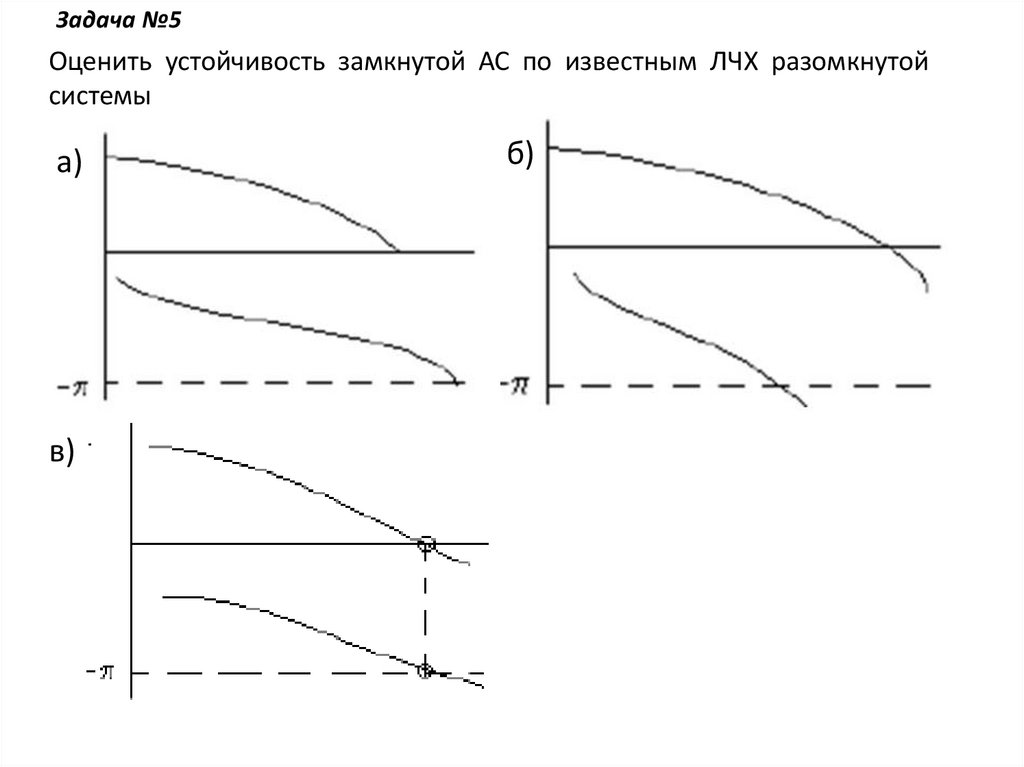
Задача №5Оценить устойчивость замкнутой АС по известным ЛЧХ разомкнутой
системы
а)
в)
б)
11.
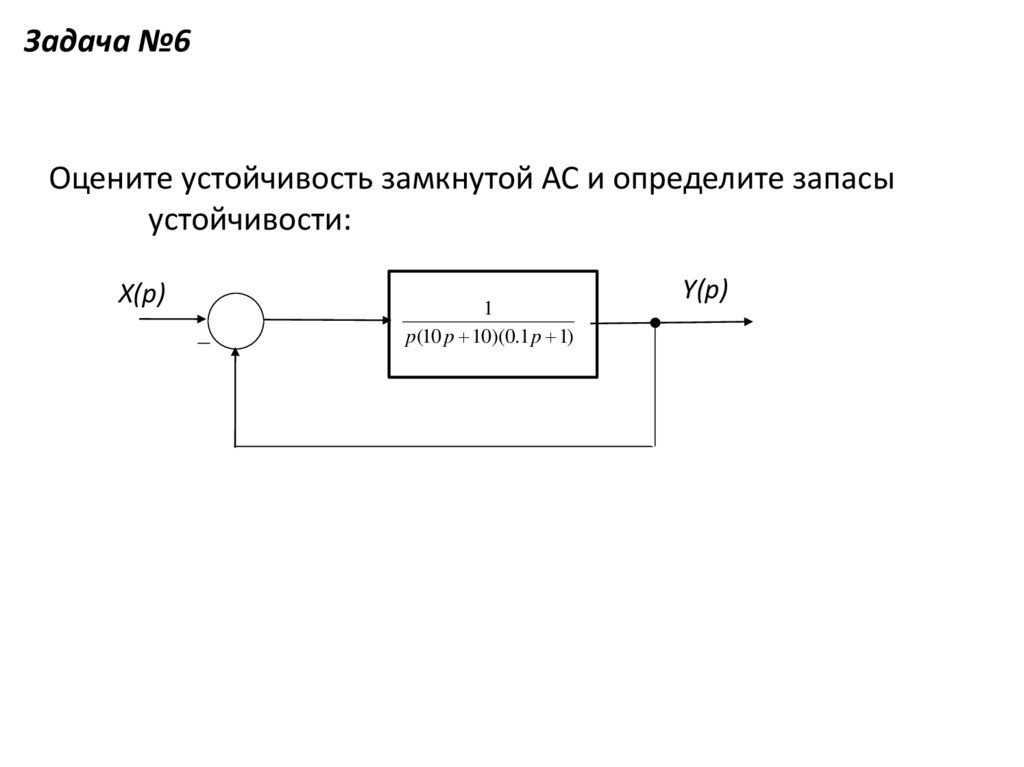
Задача №6Оцените устойчивость замкнутой АС и определите запасы
устойчивости:
X(p)
1
p(10 p 10)(0.1 p 1)
Y(p)






 Электроника
Электроника








