Похожие презентации:
Площадь треугольника
1.
Площадьтреугольника
2. Цели урока:
Изучить формулы для нахождения площадитреугольника.
Научиться применять изученные формулы
при решении задач.
3.
Какой треугольник называетсяпрямоугольным?
Как называются стороны прямоугольного
треугольника?
Что можно сказать о площадях равных фигур?
Как связанны площадь фигуры и площади ее
составляющих частей?
Какой отрезок называется высотой
треугольника?
Как вычислить площадь прямоугольника?
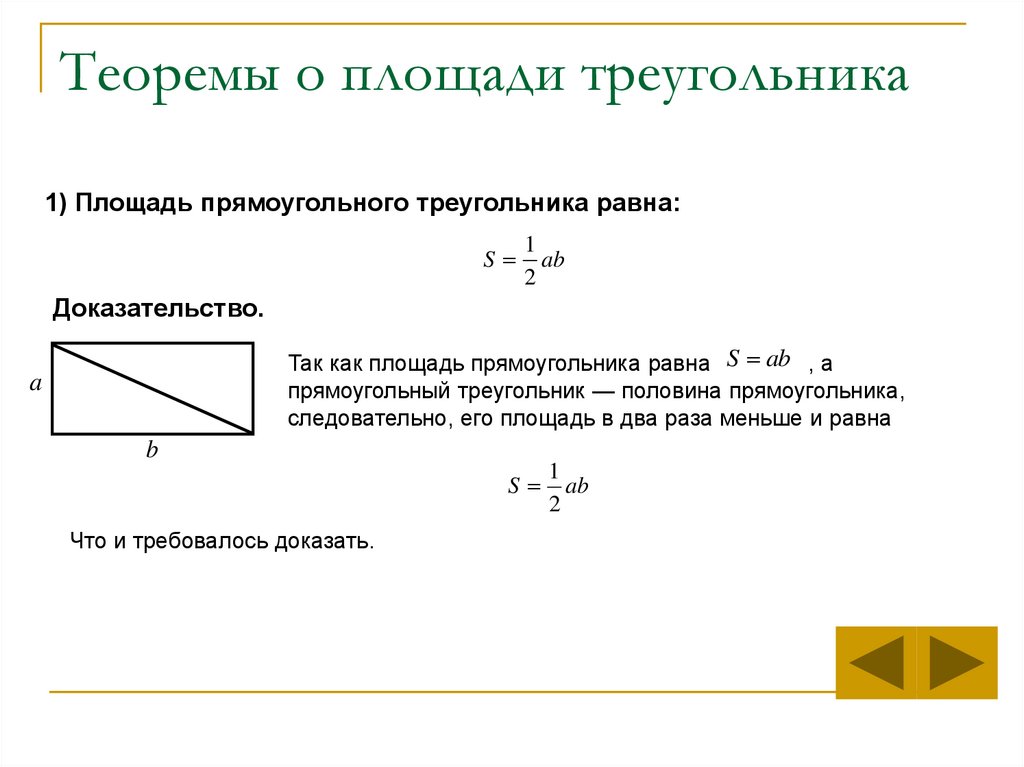
4. Теоремы о площади треугольника
1) Площадь прямоугольного треугольника равна:S
1
ab
2
Доказательство.
Так как площадь прямоугольника равна S ab , а
прямоугольный треугольник — половина прямоугольника,
следовательно, его площадь в два раза меньше и равна
a
b
S
Что и требовалось доказать.
1
ab
2
5. Теоремы о площади треугольника
2) Площадь треугольника равна:S
Доказательство.
b
S1
x
h
S2
а
с
1
ah
2
Возьмём произвольный треугольник. Проведем
высоту h, которая делит данный треугольник на
два прямоугольных треугольника.
S S1 S 2 S
Что и требовалось доказать.
1
1
1
1
hx h a x h( x a x) ha
2
2
2
2
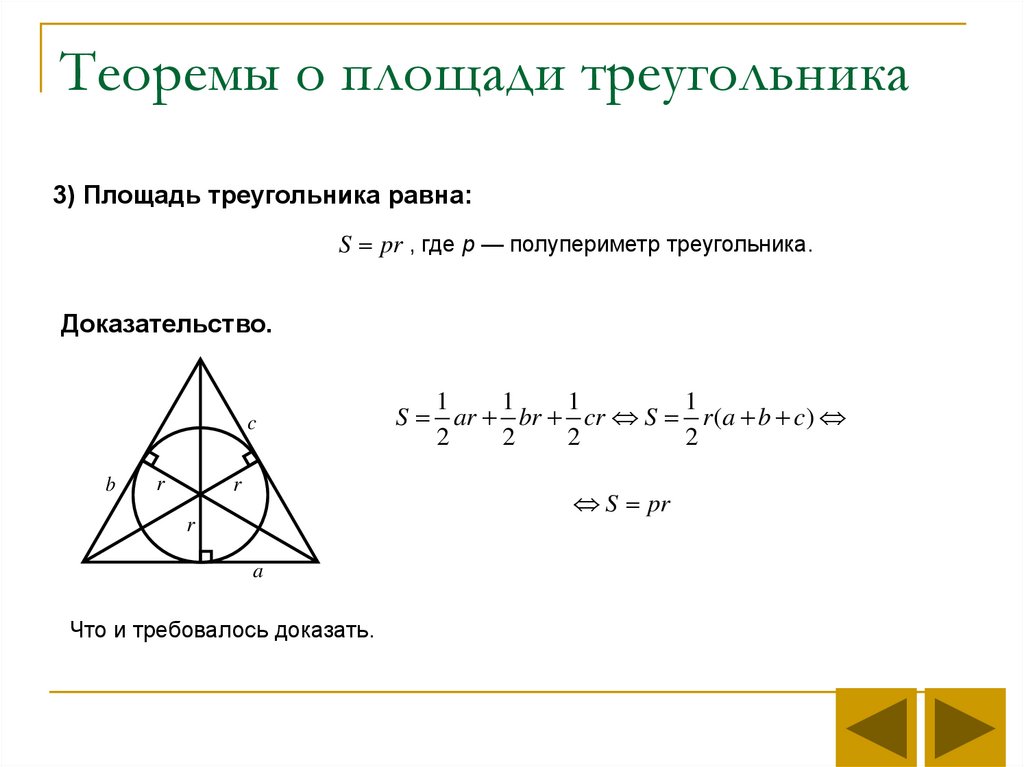
6. Теоремы о площади треугольника
3) Площадь треугольника равна:S pr , где p — полупериметр треугольника.
Доказательство.
c
b
r
r
1
1
1
1
S ar br cr S r (a b c)
2
2
2
2
S pr
r
a
Что и требовалось доказать.
7. Древние источники
Часть папируса АхмесаЧасть Древневавилонской
клинописи
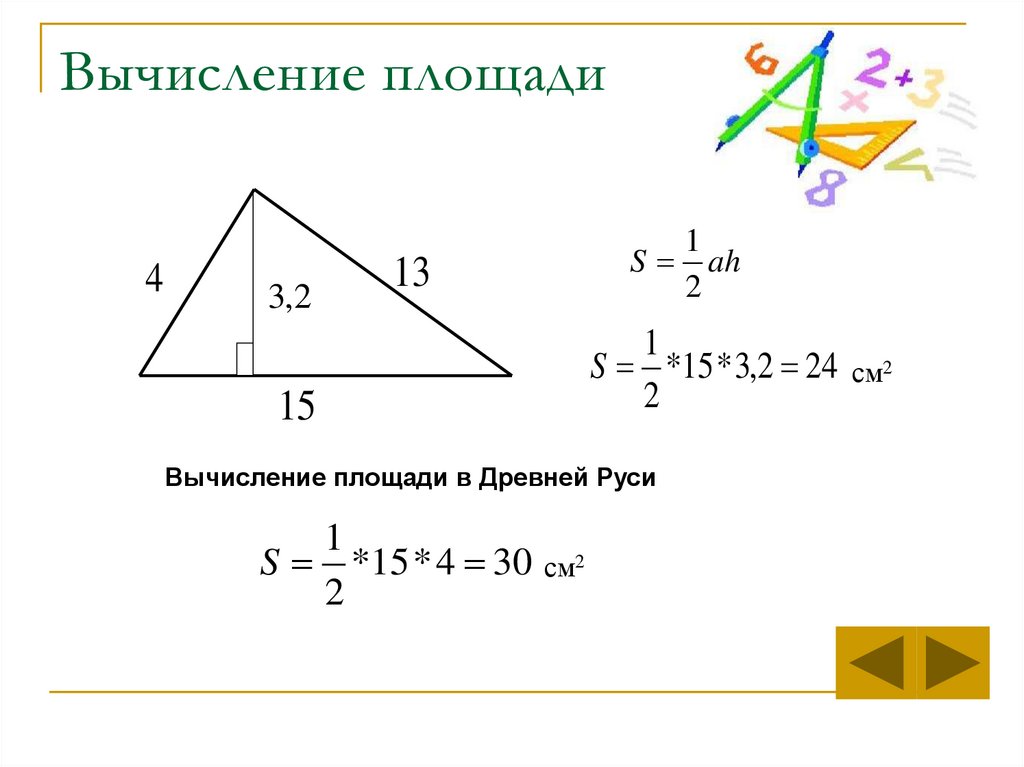
8. Вычисление площади
43,2
S
13
1
S *15 * 3,2 24
2
15
Вычисление площади в Древней Руси
1
S *15 * 4 30
2
1
ah
2
см2
см2
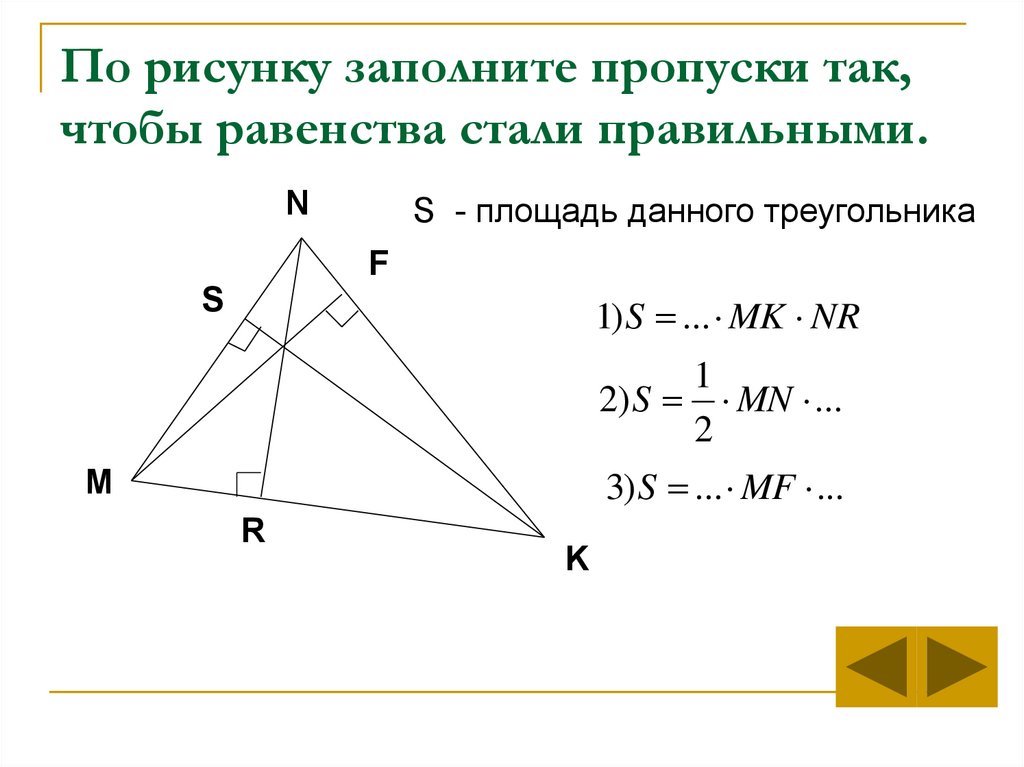
9. По рисунку заполните пропуски так, чтобы равенства стали правильными.
NS - площадь данного треугольника
F
S
1) S ... MK NR
1
2) S MN ...
2
3) S ... MF ...
M
R
K
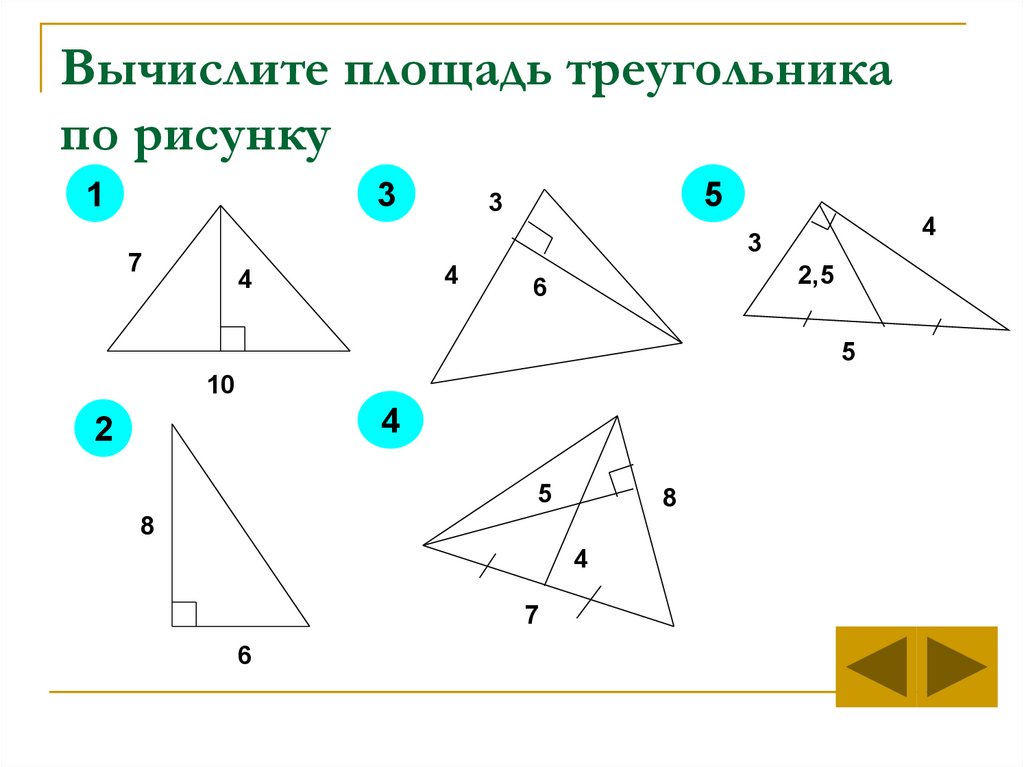
10. Вычислите площадь треугольника по рисунку
13
5
3
4
3
7
4
4
2,5
6
5
10
4
2
5
8
8
4
7
6
11.
12. Задание группам
Найдите радиус окружности,вписанной в данный треугольник.
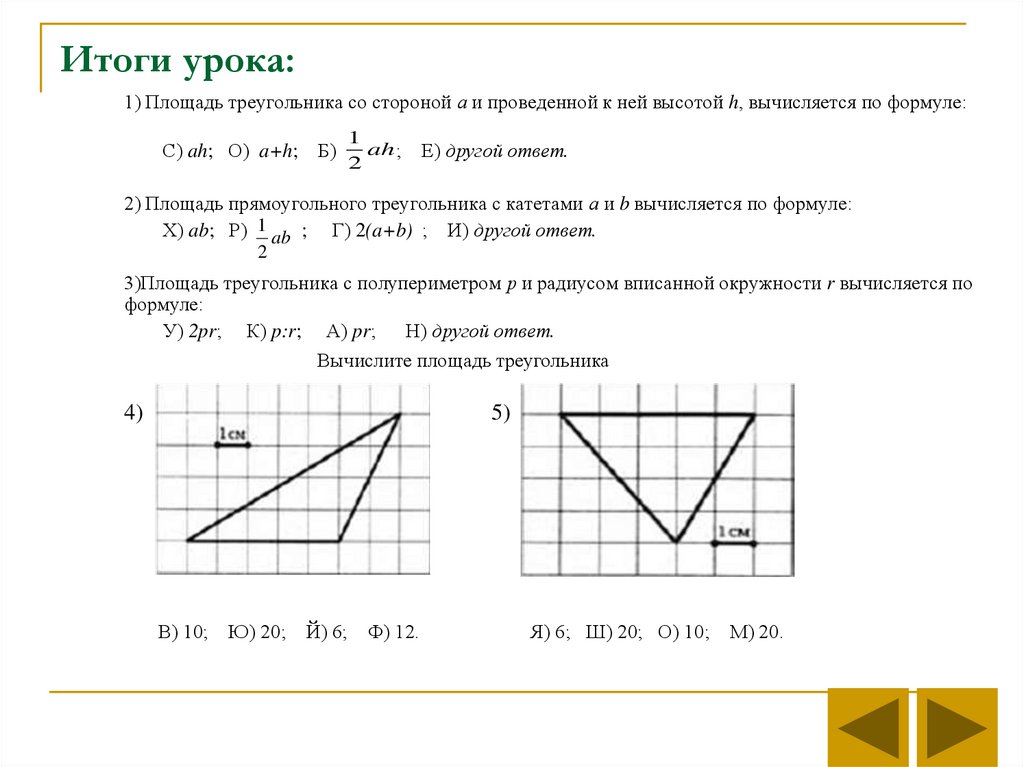
13. Итоги урока:
1) Площадь треугольника со стороной а и проведенной к ней высотой h, вычисляется по формуле:С) ah; О) a+h; Б)
1
ah ;
2
Е) другой ответ.
2) Площадь прямоугольного треугольника с катетами а и b вычисляется по формуле:
Х) ab; Р) 1 ab ; Г) 2(a+b) ; И) другой ответ.
2
3)Площадь треугольника с полупериметром р и радиусом вписанной окружности r вычисляется по
формуле:
У) 2pr; К) p:r; А) pr; Н) другой ответ.
Вычислите площадь треугольника
4)
5)
В) 10; Ю) 20; Й) 6; Ф) 12.
Я) 6; Ш) 20; О) 10; М) 20.
14. Домашнее задание:
Составить «жизненную» задачу навычисление площадей. Решить.








 Математика
Математика








