Решение задач с помощью дробных рациональных уравнений

1.

Решение задач с
помощью
дробных
рациональных
уравнений

2.

Задачи на движение
по течению и против течения реки
Собственная скорость катера Vc
Скорость течения реки Vт
по течению
Vc+Vт
против течения Vc-Vт
По течению

3.

ПЕРВАЯ!!!Катер отправился в путь в 15 часов,
прошел
7км против течения реки и сделал остановку на 2
часа. После этого он прошел еще 27 км по течению
реки и прибыл в пункт назначения в 19 часов. Найти
собственную скорость катера , если скорость
Движение
течения рекиv2, км/ч.
t, ч
s, км
км / ч
По течению
Против
течения
vсобст
vтечения
х 2
х 2
х
2
27
х 2
27
7
х 2
7

4.

Катер отправился в путь в 15 часов, прошел
7км против течения реки и сделал остановку на 2 часа.
После этого он прошел еще 27 км по течению реки и
прибыл в пункт назначения в 19 часов. Найти
собственную скорость катера , если скорость
течения реки 2 км/час.
Вычислим время движения катера
Составим уравнение
7
27
2
х 2 х 2

5. ВТОРАЯ!!!Задача

Катер прошел 8км по течению реки и 16 км против течения ,
затратив на весь путь 45 минут. Какова скорость движения
катера по течению, если собственная скорость катера равна 20 км/ч ?
Движение
v, км / ч
По течению
х 20
Против
течения
х 20
vсобст
vтечения
20
х
t, ч
8
х 20
16
х 20
s, км
8
16

6.

Зная, что катер затратил на весь путь 45 минут=
3
ч , составим уравнение:
4
8
16
3
х 20 х 20 4

7. Задачи на совместную работу

работа
производительность
время

8. ТРЕТЬЯ!!!Задача

Заказ на 180 деталей первый рабочий выполняет
на 3 часа быстрее, чем второй. Сколько деталей
в час делает второй рабочий, если известно, что
первый за час делает на 3 детали больше?
Работа
Первый
рабочий
Второй
рабочий
Производительность
х 3
х
Время
180
х 3
180
х
Объём работы
180
180
Зная, что первый рабочий выполняет на 3 часа быстрее,
чем второй, составим уравнение:

9.

180 180
3
х
х 3
Ответ :12деталей.

10. ЧЕТВЕРТАЯ!!!

При совместной работе двух кранов разгрузку баржи
закончили за 6 ч. Сколько времени потребовалось бы
каждому крану отдельно, если известно, что первому
для этого требуется на 5 ч больше, чем второму?
Работа
Первый
кран
Второй
кран
Вместе
Производительность
1
х 5
1
х
1
6
Время
Объём работы
х 5
х
6ч
1
1
1

11.

Зная, что при совместной работе двух кранов
разгрузку баржи закончили за 6 ч, составим
уравнение:
1
1
1
х х 5 6
Ответ : 15ч;10ч.

12. Задачи на смеси, растворы, сплавы

концентрация
mвещества
m раствора
концентрация
100%
Vвещества
V раствора
100%

13. ПЯТАЯ!!!Задача

В сплаве меди и цинка содержится 20 кг меди.
Когда к сплаву добавили 25 кг меди, её процентное
содержание увеличилось на 20%. Найдите
первоначальную массу сплава.
Масса металла, Масса сплава,
кг
кг
было
Медь
Цинк
стало
20 45
было
стало
х х 25
Концентрация
%
было
стало
20
45
100%
100%
х
х 25

14.

Зная, что процентное содержание меди в
сплаве увеличилось на 20%, составим
уравнение:
45
20
100% 100% 20%
х 25
х
45
20 1
х 25 х 5

15.

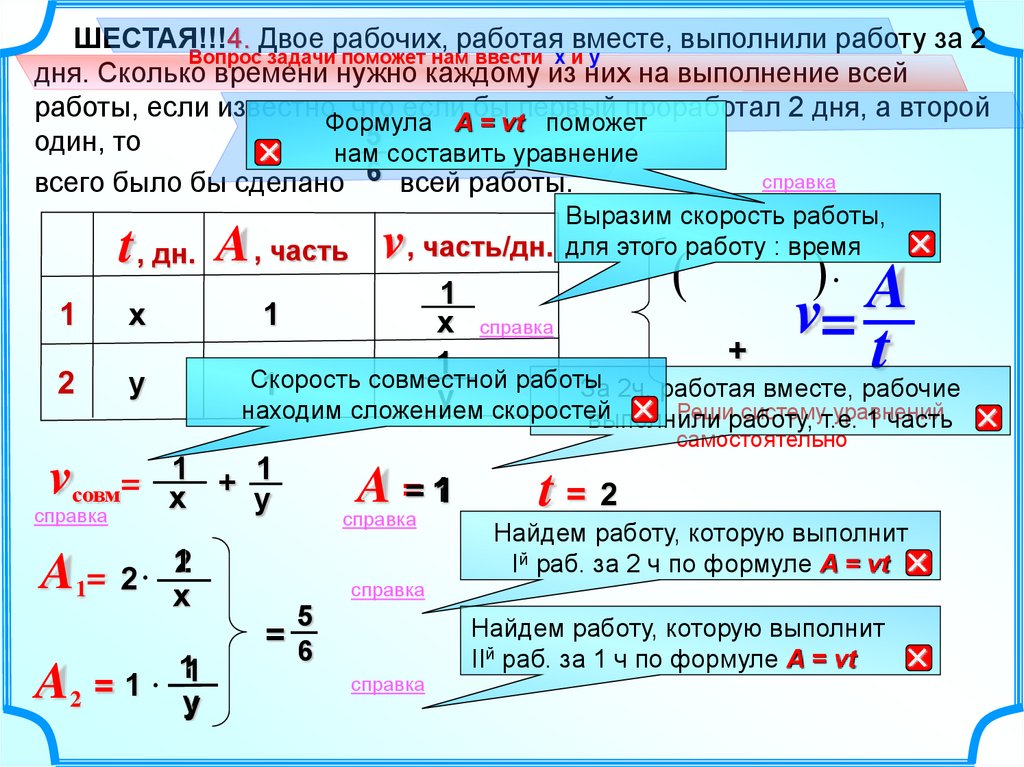
ШЕСТАЯ!!!4. Двое рабочих, работая вместе, выполнили работу за 2
Вопрос задачи поможет нам ввести х и у
дня. Сколько времени нужно каждому из них на выполнение всей
работы, если известно, что если бы первый проработал 2 дня, а второй
Формула A = vt поможет
один, то
нам56 составить уравнение
справка
всего было бы сделано
всей работы.
t , дн. A , часть v
1
х
2
у
Выразим скорость работы,
, часть/дн. для этого работу : время
A
v
1
1
х справка
+
1
Скорость
совместной работы
1
За 2ч, работая вместе, рабочие
у
находим сложением скоростей Реши систему уравнений
=t
выполнили работу, т.е. 1 часть
самостоятельно
vсовм=
справка
A1= 2
A2 = 1
1 + 1
х
у
1
2
х
11
у
A=1
справка
справка
5
=6
справка
t=2
Найдем работу, которую выполнит
Iй раб. за 2 ч по формуле A = vt
Найдем работу, которую выполнит
IIй раб. за 1 ч по формуле A = vt

16.

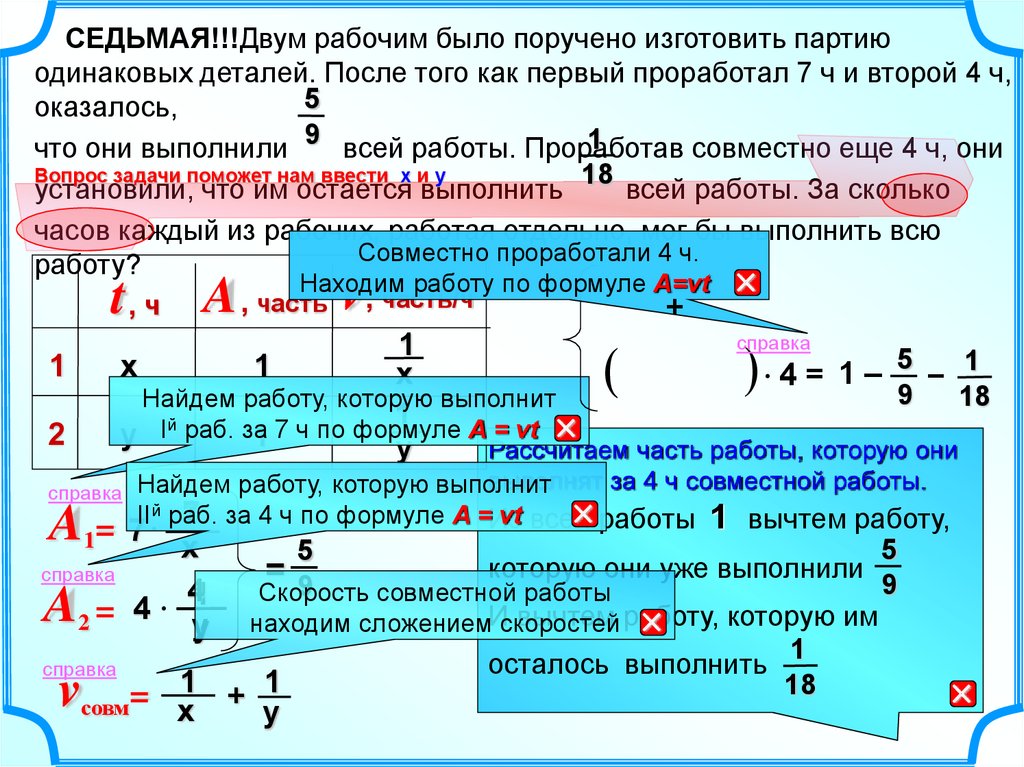
СЕДЬМАЯ!!!Двум рабочим было поручено изготовить партию
одинаковых деталей. После того как первый проработал 7 ч и второй 4 ч,
5
оказалось,
1
что они выполнили 9 всей работы. Проработав
совместно еще 4 ч, они
Вопрос задачи поможет нам ввести х и у
18
установили, что им остается выполнить
всей работы. За сколько
часов каждый из рабочих, работая отдельно, мог бы выполнить всю
Совместно проработали 4 ч.
работу?
Находим работу по формуле А=vt
, часть/ч
,
часть
,ч
+
1
2
справка
1
х
1
х
4 = 1 – 59 – 1
18
Найдем работу, которую выполнит
1
A = vt
у Iй раб. за1 7 ч по формуле
у
Рассчитаем часть работы, которую они
справка
выполнят за 4 ч совместной работы.
Найдем работу, которую выполнит
1
7 за 4 ч по формуле A =Из
IIй раб.
vt всей
работы 1 вычтем работу,
A1= 7
х
справка
41
4
2=
у
A
справка
v
A
t
vсовм=
1
х
5
5
которую
они
уже
выполнили
=9
9
Скорость
совместной работы
вычтем работу,
которую им
находим сложениемИскоростей
1
осталось выполнить
18
+ 1
у

17.

4 5
7
х + у = 9
1
1
5
1
4
=
1
–
–
+
х
у
9 18
4 5
7
х + у = 9
4
4 17 – 5 – 1
х + у = 18 9 18
–
7
4
5
х + у =9
3
3
х = 18
7
18 +
4
у =
х = 18
4
3
=
у
18
у = 24
4
5
у =9
5
– 7
9 18
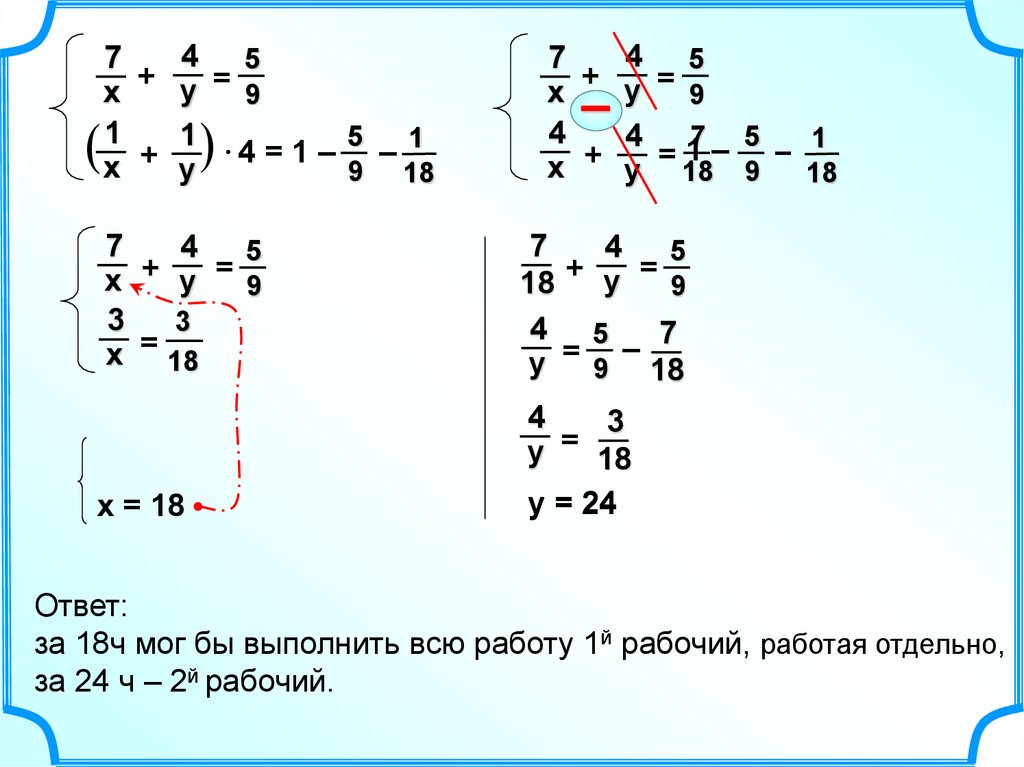
Ответ:
за 18ч мог бы выполнить всю работу 1й рабочий, работая отдельно,
за 24 ч – 2й рабочий.

18.

СЕМЬ задач
решили?!
МОЛОДЦЫ!!!

19.

Далее просто
смотрим и
вникаем!!!

20.

. Из городов A и B навстречу друг другу выехали мотоциклист и
велосипедист. Мотоциклист приехал в B на 3 часа раньше, чем
в задаче не
дано
велосипедист приехал в A, аЕсли
встретились
они
через 48 минут после
расстояние, очень удобно считать
выезда. Сколько часов затратил на путь из B в A велосипедист?
весь путь, как 1 целая часть.
на весь путь
t, ч S, часть v, часть/ч
Велосипедист
B-A
х
1
Мотоциклист
A-B
у
1
v
навстречу
1
х часть/ч
B
1
1
х + у
t
встречи
48
60
1
х
1
у
x–у=3
1 4
1
=1
х + у 5
S
1
4 ч
5
1 часть
1
у часть/ч
A
Ответ: 4 ч

21.

6. При испытании двух двигателей было установлено, что первый
израсходовал 300 г, а второй 192 г бензина, причем второй работал на
2 ч меньше, чем первый. Первый двигатель затрачивал в час на 6 г
бензина больше, чем второй. Какое количество бензина в час
расходовал каждый из двигателей?
Составить
можнокаждого
иначе…
Начнем суравнение
времени работы
двигателя (ч)
t ,ч
1
2
х+2
A, г
300
справка
справка
х
192
справка расход горючего для каждого
Общий
двигателя – это А (г)
v, г/ч
Выразим скорость работы,
300 для этого работу : время
х+2
192
х
A
v=
t
300
192
=
х+2
х на+66г/ч
>
Но, решив это уравнение, придется сделать еще дополнительные
действия, чтобы ответить на вопрос задачи.

22.

№113367. Расстояние между городами A и B равно 390 км. Из
города A в город B выехал автомобиль, а через 30 минут следом за
ним со скоростью 70 км/ч выехал мотоциклист, догнал автомобиль
в городе C и повернул обратно. Когда он вернулся в A, автомобиль
прибыл в B. Найдите расстояние от A до C. Ответ дайте в
километрах.
70 км/ч
30 мин
S
А
C
390
В
Решение. Обозначим расстояние от А до С за S км, скорость
автомобиля – за x км/ч. Тогда время движения на этом
участке можно выразить уравнением:
S
S
1
для мотоциклиста
для автомобиля
x 70 2

23.

А время движения автомобиля на всем участке от А до В:
2S 1 390
70 2
х
для мотоциклиста
S
1
S
x 70 2 ,
2S 1 390 ;
70 2
х
S S 35
x 70 ,
2S 35 390 ;
70
х
для автомобиля
70S
х
,
S 35
2S 35 390 S 35 ;
70
70S
2S 35 390 S 35
70
70S
70S
2S 2 35S 390S 390 35
2S 2 355S 13650 0
S 210
S 32,5 – не удовл-ет условию S > 0
S 210
Ответ: 210.

24.

6. При испытании двух двигателей было установлено, что первый
израсходовал 300 г, а второй 192 г бензина, причем второй работал на
2 ч меньше, чем первый. Первый двигатель затрачивал в час на 6 г
бензина больше, чем второй. Какое количество бензина в час
расходовал каждый из двигателей?
Решим
эту сже
задачу работы
с помощью
системы уравнений…
Начнем
времени
каждого
двигателя (ч)
Введем переменную для расхода
горючего в час (г/ч)
1
2
t, ч
v, г/ч A, г
х+2
y+6
справка
справка
х
y
(х+2)(у+6) = 300,
ху = 192.
справка
(х+2)(у+6) =
ху
Найдем общий расход бензина
300 по формуле A = vt
= 192

25.

(х+2)(у+6) = 300,
ху+6х+2у+12 = 300,
ху = 192;
ху = 192
192;
192+6х+2у+12 = 300,
ху = 192;
t, ч
х+2
3х+у=
1 48,
6х+2у= 96, : 2
ху = 192;
v, г/ч A, г
y ху = 192;
ху
y+6 у=(х+2)(у+6)
48 – 3х , = 300
ху =2192; х
= 192
3х2 – 48х + 192 = 0
D
= 242 – 3 192 = 0
4
24 + 0
x=
=8
3
у = 48 – 3 8 = 24
у= 48 – 3х ,
у = 24,
х(48 – 3х) = 192;
х = 8.
48х – 3х2 = 192
Теперь ответим на вопрос задачи.
24 г/ч расходует 2й двигатель,
30 г/ч – 1й двигатель.