Похожие презентации:
Правило быстрого возведения в квадрат суммы или разности
1.
“Чтобы переварить знания надопоглощать их с аппетитом”
Анатоль Франс
французский писатель
2.
Прочитайте следующие выражения, используя слова:«сумма», «разность», «квадрат», «куб», «произведение»
3
b)
(a +
2
2
a +b
a·b
2ab
2
(a + b)
(a – b)
2
3.
Запишите следующие словосочетания на математическомязыке:
квадрат числа семь
квадрат выражения 2у
произведение a и 3b
удвоенное произведение 7n и 3k
квадрат суммы выражений 5x и 4y
квадрат разности выражений 3х и 1.
4.
27
2
(2у)
3ab
(5x +
(3х
2
4y)
2
-1) .
5.
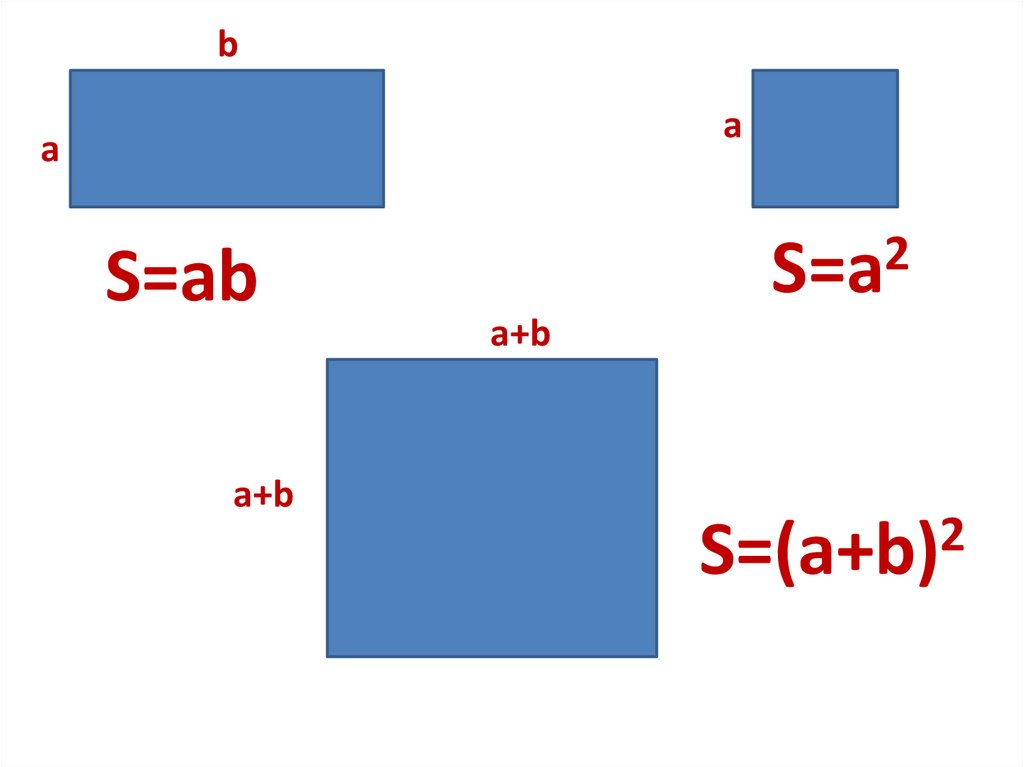
ba
a
S=ab
a+b
2
S=a
a+b
2
S=(a+b)
6.
( 3+х)(х+2)=3x+6+х2+2x=х2+5x+6(5-y)(4-y)=20-5y-4y-y2=20-9y-y2
2
2
(a+8)(a+8)=a +8a+8a+64=a +16a+64
2
2
(4-x)(4-x)=16-4x-4x+x =16-8x+x
2
2
(5-y)(4-y)=20-5y-4y+y =20-9y+y
7.
( 3+х)(х+2)=3x+6+х2+2x=х2+5x+6(5-y)(4-y)=20-5y-4y+y2=20-9y+y2
2
2
(a+8)(a+8)=a +8a+8a+64=a +16a+64
2
2
(4-x)(4-x)=16-4x-4x+x =16-8x+x
2
(a+8)
2
(4-x)
8.
2(5x
–
2
7y)
Возведите двучлены в квадрат,
не используя
правила умножения многочленов:
а) (а
+ b)2;
б) (а−b)2
9.
Цель урока:узнать правило быстрого возведения в
квадрат суммы или разности.
Научиться пользоваться алгоритмом
возведения в квадрат суммы и разности двух
выражений.
.
10.
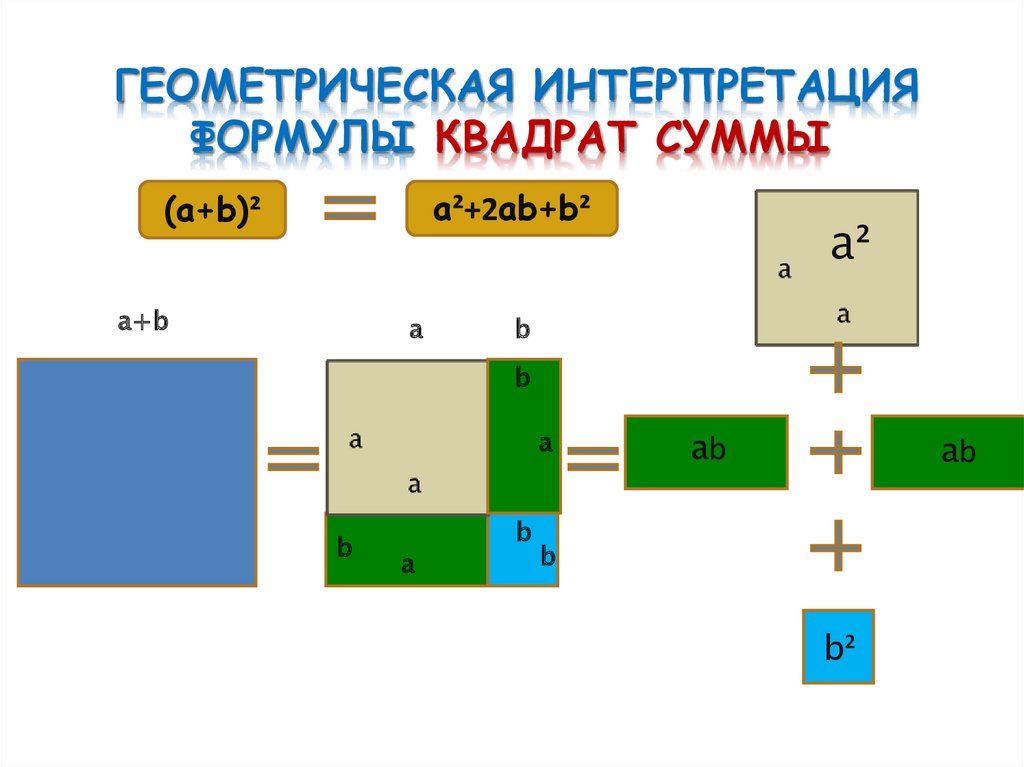
ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯФОРМУЛЫ КВАДРАТ СУММЫ
a²+2ab+b²
(a+b)²
a+b
a
b
b
b
a
b
a
a²
b
ab
ab
b
b²
11.
ИССЛЕДОВАТЕЛЬСКАЯРАБОТА
№
I
II
1.
(y + b) (y +b)
2.
(с + d ) (c +d)
3.
(x – y) (x – y)
4.
(m - n) (m- n)
(y + b) 2
(c + d)2
(x – y)2
(m - n)2
III
y 2 + 2yb + b2
c2 + 2cd + d2
x2 – 2xy + y2
m2 – 2mn + n2
12.
ФОРМУЛЫ СОКРАЩЁННОГО УМНОЖЕНИЯквадрат суммы
(а+b)² = а² +2аb+b²
квадрат разности
(а-b)² = а² -2аb+b²
Как вы думаете, почему данные формулы называются
формулами сокращённого умножения?
13.
(а +2
в)
=
2
а
+ 2ав +
2
в
Квадрат суммы двух
выражений равен квадрату
первого выражения плюс
удвоенное произведение
первого и второго выражений
плюс квадрат второго
выражения.
14.
(а -2
в)
=
2
а
- 2ав +
2
в
Квадрат разности двух
выражений равен квадрату
первого выражения минус
удвоенное произведение
первого и второго выражений
плюс квадрат второго
выражения.
15.
Заполни пропуски(поставь знак «+» или «-»):
1. (р – а)² = р² □2ра □а²
2. (8 – у)² = 64 □16у□у²
3. (s + z)² = s²□2sz□z²
4. (t + f)² = t² □2tf □f²
5. (d – m)(d – m) = d²□2dm□m²
(а+b)² = а² +2аb+b²
(а-b)² = а² -2аb+b²
16.
Заполни пропуски(поставь знак «+» или «-»):
1. (р – а)² = р² –2ра +а²
2. (8 – у)² = 64 – 16у + у²
3. (s + z)² = s² + 2sz + z²
4. (t + f)² = t² + 2tf + f²
5. (d – m)(d – m) = d² – 2dm + m²
(а+b)² = а² +2аb+b²
(а-b)² = а² -2аb+b²
17.
ФОРМУЛЫ СОКРАЩЁННОГО УМНОЖЕНИЯквадрат суммы
(а+b)² = а² +2аb+b²
квадрат разности
(а-b)² = а² -2аb+b²
Алгоритм.
18.
Алгоритм2
(5x
–
2
7y)
П 32, пример1, пример 2.
№799(а, б, е, ж)
19.
Преобразуйт е в многочлен(a 3)
2
a 2 a 3 3
2
2
a 6a 9.
2
a b a b
a 2 b 2 a b 2 a 2 2ab b 2 a b 2 a 2 2ab b 2
20.
Преобразуйт е в многочлен(x 4)
2
2
x 2 x 4 4
2
x 8 x 16.
2
a b a b
a 2 b 2 a b 2 a 2 2ab b 2 a b 2 a 2 2ab b 2
21.
Преобразуйт е в многочлен(2 x y )
2
(2 x) 2 2 x y y
2
2
4 x 4 xy y .
2
a b a b
2
a 2 b 2 a b 2 a 2 2ab b 2 a b 2 a 2 2ab b 2
22.
Самостоятельная работа1 вариант
2 вариант
Представьте в виде многочлена:
Заполни пропуски (поставь знак «+» или «-»):
(р – а)² = р² □2ра □а²
(s + z)² = s²□2sz□z²
(8 – у)² = 64 □16у□у²
(t - 10)² = t² □20t □100
23.
Проверим :1 вариант
81 18a a 2 .
2
64 16b b .
9 y 24 y 16.
2
(р – а)² = р²- 2ра +а²
2 вариант
4 4 y y2.
2
36 12c с .
2
4 x 36 x 81.
(s + z)² = s²+2sz+z²
(8 – у)² = 64 - 16у+у² (t - 10)² = t² - 20t +100
5 – «5»; 4 – «4»; 3 – «3».
24.
Проверим :1 вариант
1)(9 a ) 2 92 2 9 a a 2
2)(8 b) 2 82 2 8 b b 2
81 18a a .
2
64 16b b .
2
3)(3 y 4) 2 (3 y ) 2 2 3 y 4 42
9 y 2 24 y 16.
2 вариант
1)(2 y ) 2 2 2 y y 4 4 y
2
2
2
2
2
6
2
6
c
с
2)(6 c)
2
y .
36 12c с .
2
2
(
2
x
)
2
2
x
9
9
3)(2 x 9)
2
2
2
4 x 36 x 81.
2
25.
Предлагаю на выбор одно из заданий.№810а б,
№ 818а,
№820 а
26.
ФОРМУЛЫ СОКРАЩЁННОГО УМНОЖЕНИЯквадрат суммы
(а+b)² = а² +2аb+b²
квадрат разности
(а-b)² = а² -2аb+b²
Как вы думаете, почему данные формулы называются
формулами сокращённого умножения?
27.
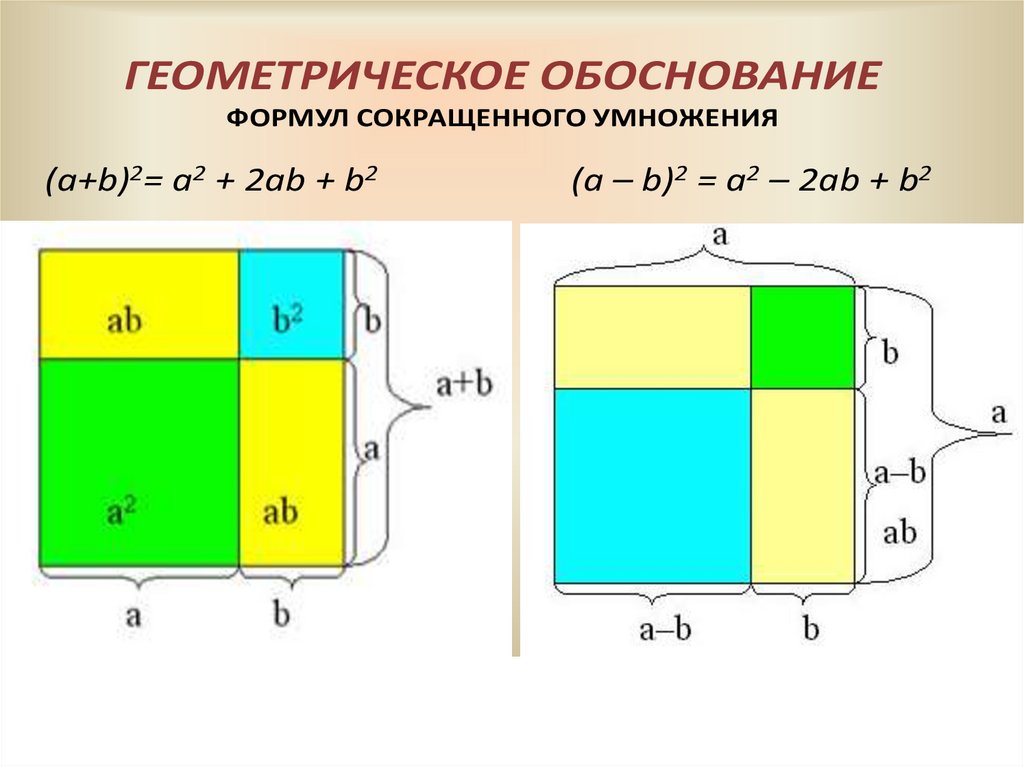
ГЕОМЕТРИЧЕСКОЕ ОБОСНОВАНИЕФОРМУЛ СОКРАЩЕННОГО УМНОЖЕНИЯ
(a+b)2= a2 + 2ab + b2
(a – b)2 = a2 – 2ab + b2
28.
Домашнее задание.п 32 (примеры 1,2, формулы1, 2)
№800, 801, 803 (а-г), 830
29.
РефлексияСамым интересным сегодня на уроке было______
Самым сложным для меня сегодня было________
Сегодня я понял____________
Сегодня я научился_________
Сегодня я задумался_________
Сегодняшний урок показал мне_________
На будущее мне надо иметь в виду_________



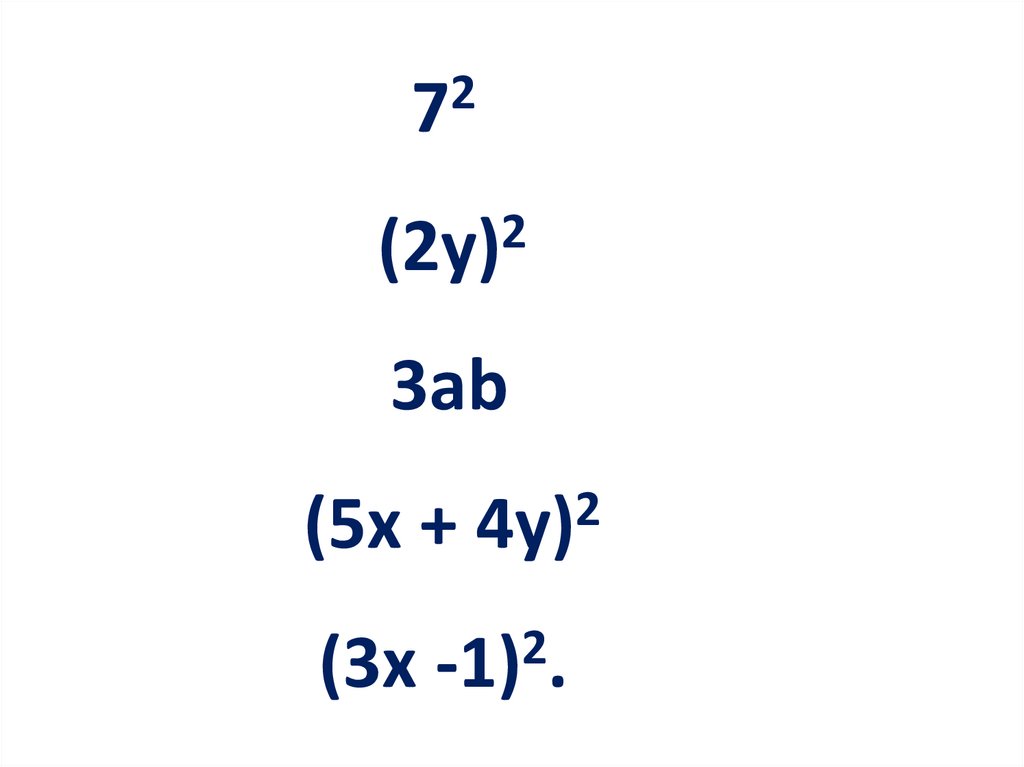
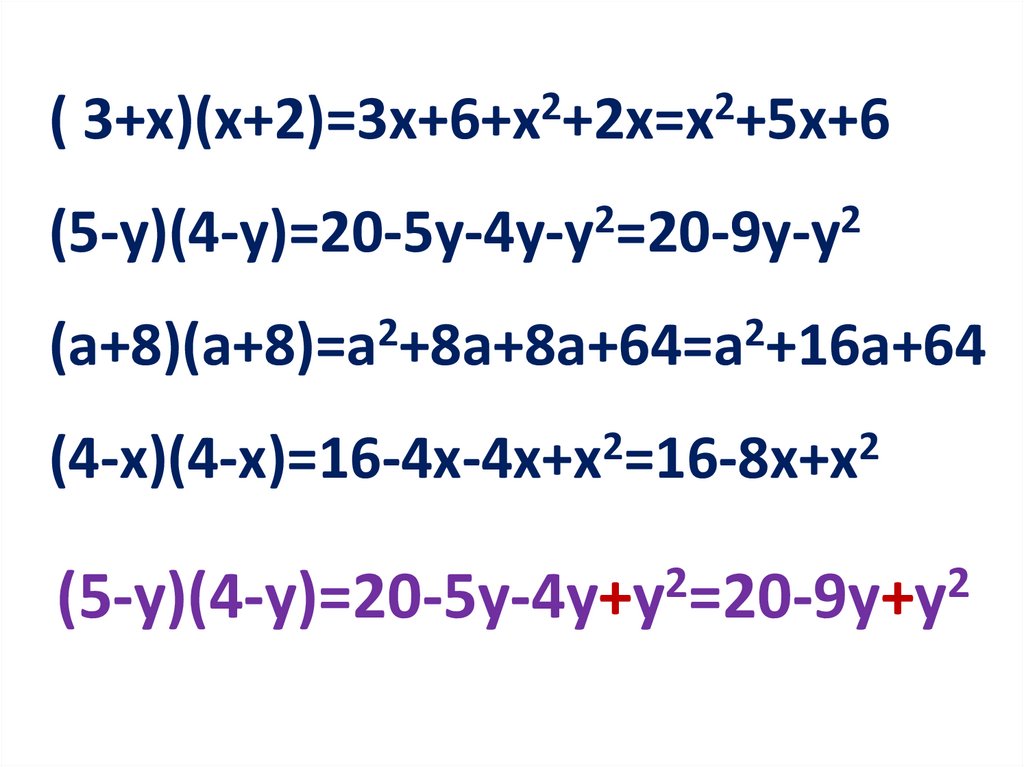
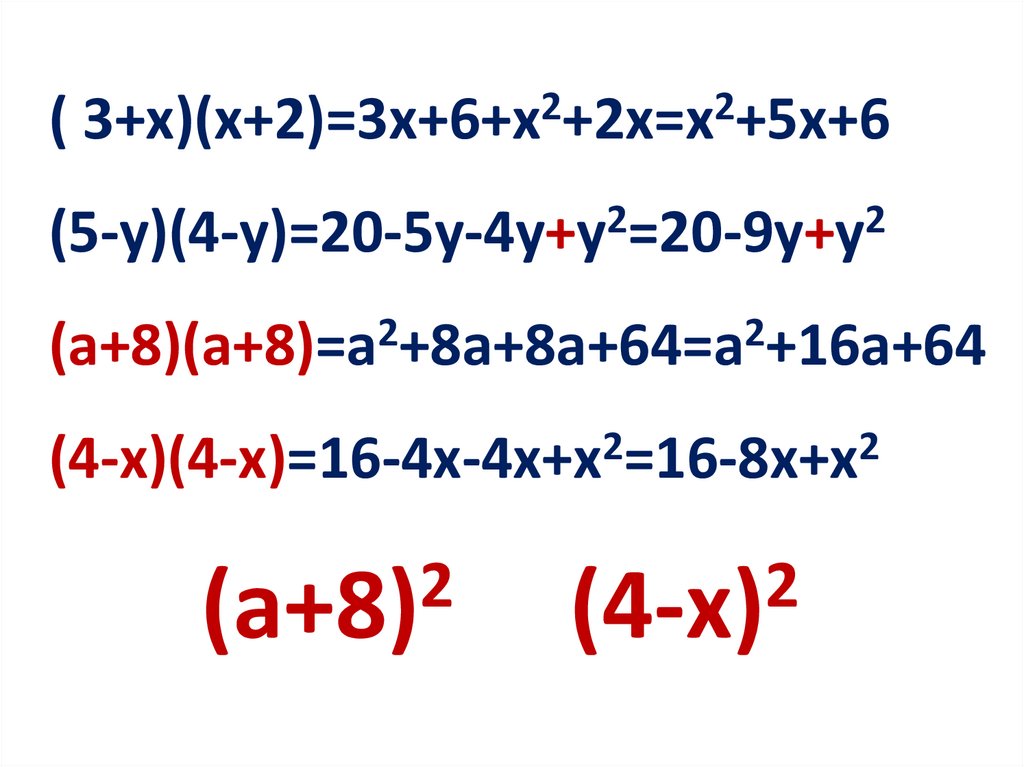




















 Математика
Математика








