Неравенства. Рациональные, иррациональные, показательные и тригонометрические неравенства

1.

Неравенства. Рациональные,
иррациональные,
показательные и
тригонометрические
неравенства. Основные приемы
их решения.

2.

Цель:
рассмотреть основные приемы решения
рациональных, иррациональных,
показательных неравенств, показать
алгоритм решения тригонометрических
неравенств с использованием
единичной окружности научиться
решать простейшие
тригонометрические неравенства,
развить умения обобщать полученные
знания.

3.

4.

5.

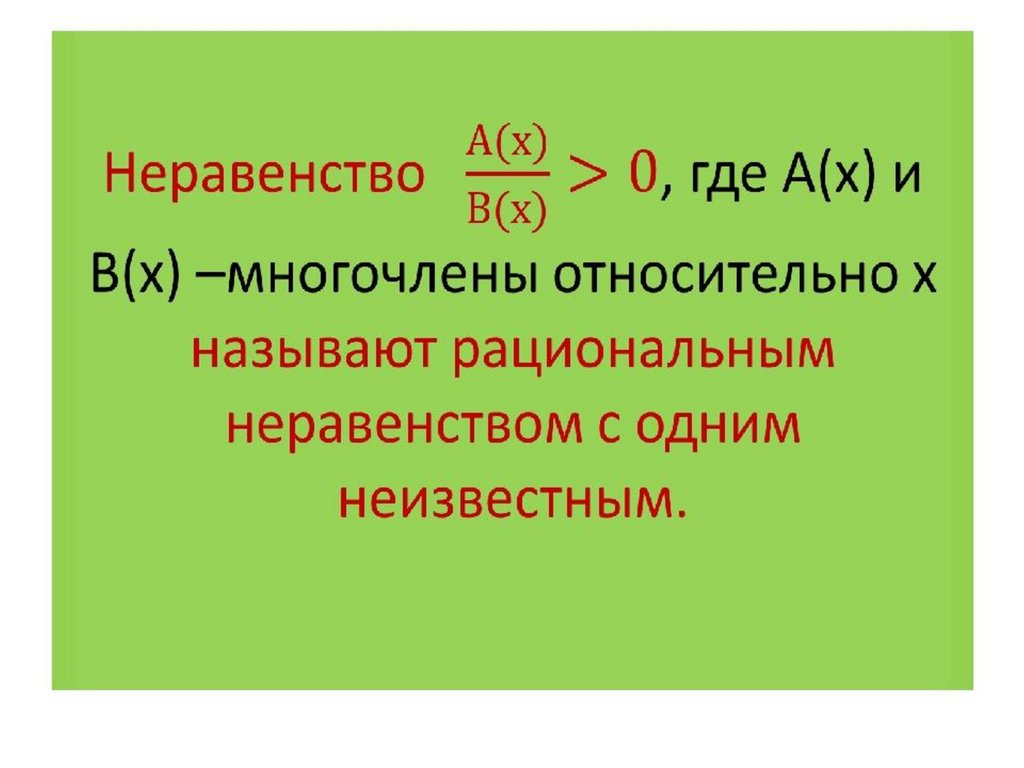
Рациональные
неравенства

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

Иррациональные
неравенства

24.

25.

26.

27.

28.

29.

30.

31.

32.

Показательные
неравенства

33.

34.

35.

36.

37.

38.

39.

40.

41.

42.

43.

44.

45.

46.

47.

Тригонометрические
неравенства
неравенства cost >a,
cost ≥ a, cost <a, cost ≤ a
неравенства sint >a,
sint ≥ a, sint <a, sint ≤ a

48.

Неравенство sint > a
Алгоритм решения
y
1
1. Отметить на оси ординат
интервал y > a.
2.Выделить дугу окружности,
соответствующую интервалу.
3. Выбрать положительный
t1
π-t1
a
0
-1
x
обход дуги ( против часовой
стрелки)
4.Записать числовые значения
граничных точек, при этом
начало дуги- меньшее
значение
5. Записать общее решение
неравенства.

49.

3
2
sin x
y
3
0 ,8
2
и соответствующие точки на
окружности.
2
2. Выделяем верхнюю часть
окружности (обход совершаем
против часовой стрелки).
1.
На Оу отмечаем значение
2
x
4
3
3.
3
2
3
Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее значение.
4
2 k ;
2 k
4. Ответ: х
3
3
49

50.

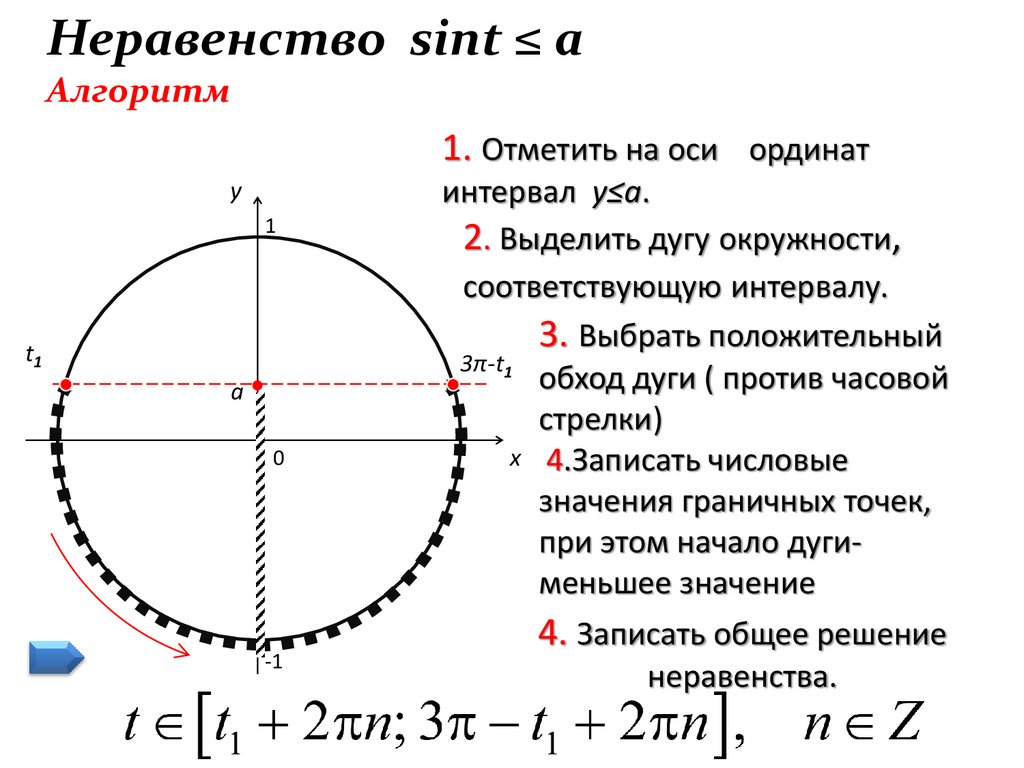
Неравенство sint ≤ a
Алгоритм
1. Отметить на оси ординат
y
1
t1
a
0
-1
интервал y≤a.
2. Выделить дугу окружности,
соответствующую интервалу.
3. Выбрать положительный
3π-t1
обход дуги ( против часовой
стрелки)
x 4.Записать числовые
значения граничных точек,
при этом начало дугименьшее значение
4. Записать общее решение
неравенства.

51.

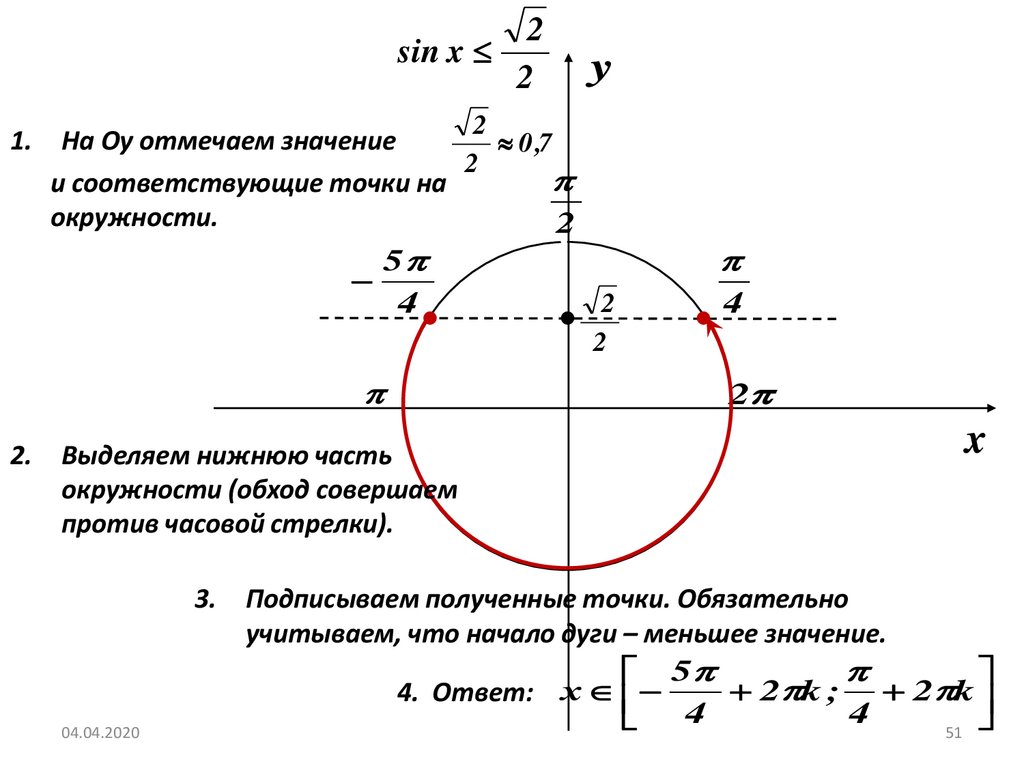
sin x
1.
y
2
На Оу отмечаем значение
0 ,7
2
и соответствующие точки на
окружности.
2
5
4
2.
2
2
2
2
4
2
x
Выделяем нижнюю часть
окружности (обход совершаем
против часовой стрелки).
3.
04.04.2020
Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее значение.
5
2 k ; 2 k
4. Ответ: х
4
4
51

52.

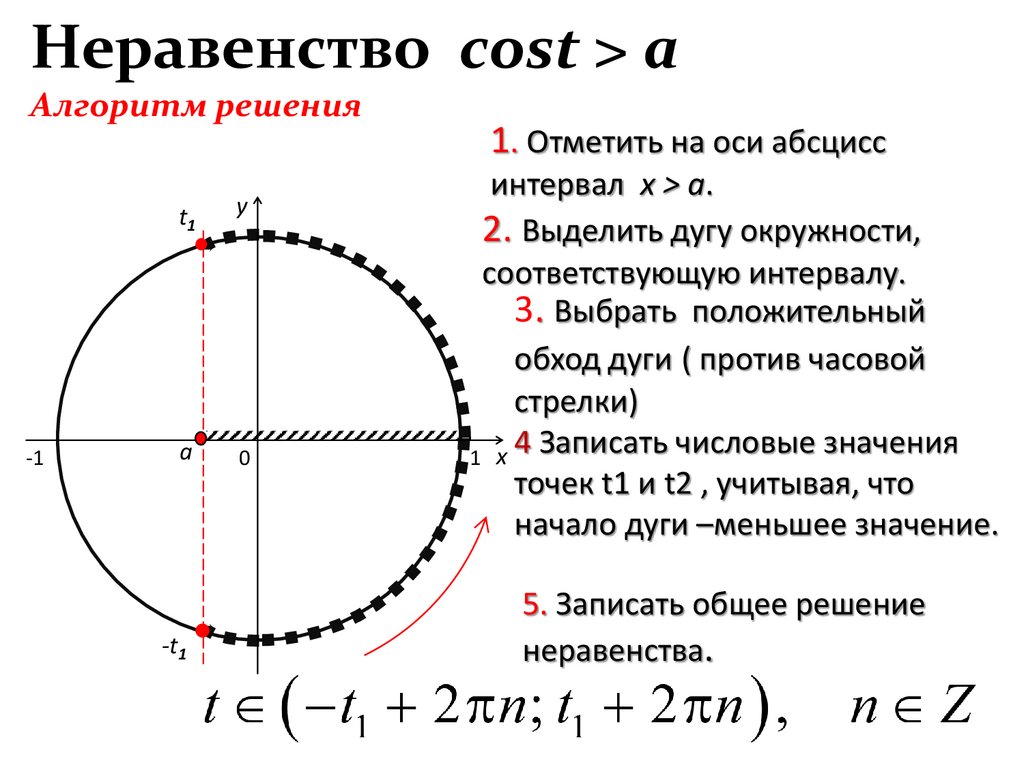
Неравенство cost > a
Алгоритм решения
-1
t1
y
a
0
-t1
1. Отметить на оси абсцисс
интервал x > a.
2. Выделить дугу окружности,
соответствующую интервалу.
3. Выбрать положительный
обход дуги ( против часовой
стрелки)
4 Записать числовые значения
1 x
точек t1 и t2 , учитывая, что
начало дуги –меньшее значение.
5. Записать общее решение
неравенства.

53.

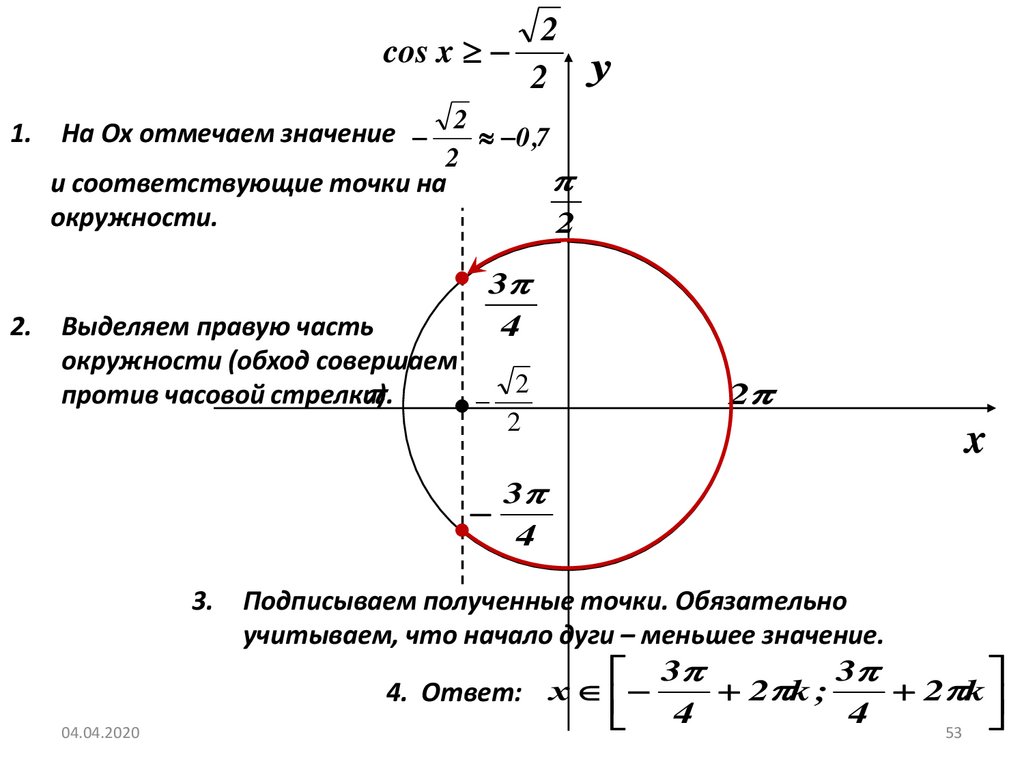
cos x
1.
2.
2
2 y
На Ох отмечаем значение 2 0 ,7
2
и соответствующие точки на
окружности.
2
3
4
Выделяем правую часть
окружности (обход совершаем
2
против часовой стрелки).
2
3.
04.04.2020
2
x
3
4
Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее значение.
3
3
2 k ;
2 k
4. Ответ: х
4
4
53

54.

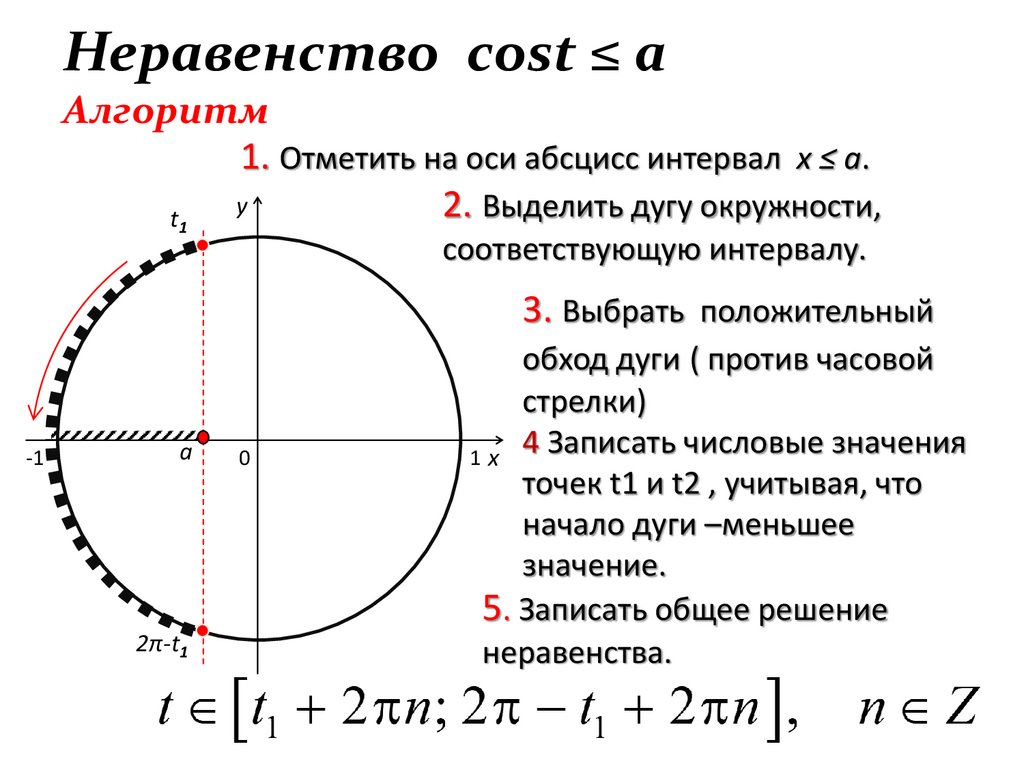
Неравенство cost ≤ a
Алгоритм
1. Отметить на оси абсцисс интервал x ≤ a.
y
2. Выделить дугу окружности,
t1
соответствующую интервалу.
3. Выбрать положительный
-1
a
2π-t1
0
обход дуги ( против часовой
стрелки)
4 Записать числовые значения
1x
точек t1 и t2 , учитывая, что
начало дуги –меньшее
значение.
5. Записать общее решение
неравенства.

55.

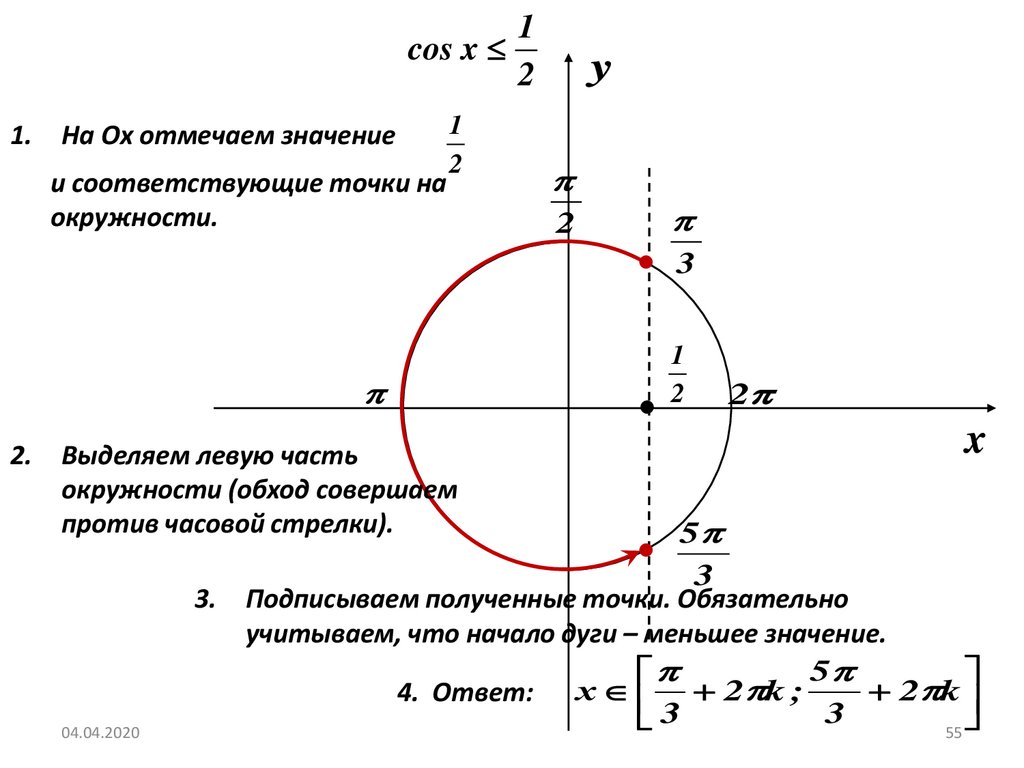
1
cos x
2
1.
На Оx отмечаем значение
и соответствующие точки на
окружности.
1
2
y
2
3
2.
Выделяем левую часть
окружности (обход совершаем
против часовой стрелки).
3.
04.04.2020
1
2
2
x
5
3
Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее значение.
5
х 2 k ;
2 k
4. Ответ:
3
3
55

56.

Решите неравенства

57.

Домашнее задание:
Решите неравенства