Задачи, приводящие к понятию производной

1. Задачи, приводящие к понятию производной.

10
9
8
7
6
5
4
3
2
1
0
Y
X
1
2
3
4
5
6
7
8
9
10

2.

► К понятию производной можно прийти,
рассматривая, например, такое широко
используемое в физике понятие, как
мгновенная скорость неравномерно
движущегося тела.
► Мгновенной скоростью тела называют
скорость, которую оно имеет в данный
момент времени (в данной точке траектории)

3. Производная

Центральные понятия дифференциального исчисления
– производная и дифференциал возникли при
рассмотрении большого числа задач естествознания и
математики, приводивших к вычислению пределов
одного и того же типа. Важнейшие среди них –
физическая задача определения скорости
неравномерного движения и геометрическая задача
построения касательной к кривой.

4. Задача 1 (о скорости движения).

По прямой, на которой заданы начало отсчета,
единица измерения (метр) и направление,
движется некоторое тело (материальная точка).
• Закон движения задан формулой s=s (t), где t —
время (в секундах), s (t) — положение тела на
прямой (координата движущейся материальной
точки) в момент времени t по отношению к
началу отсчета (в метрах).
• Найти скорость движения тела в момент
времени t (в м/с).

5.

Пусть в некоторый момент времени времени t,
точка занимает положение М: OM = x= S(t),
через время Δt, т.е. в момент t + Δt, точка
окажется в M1, где
ОM1 = S + ΔS = S(t +Δt).
За время Δt, точка проходит путь
ΔS = S(t + Δt) – S(t).

6.

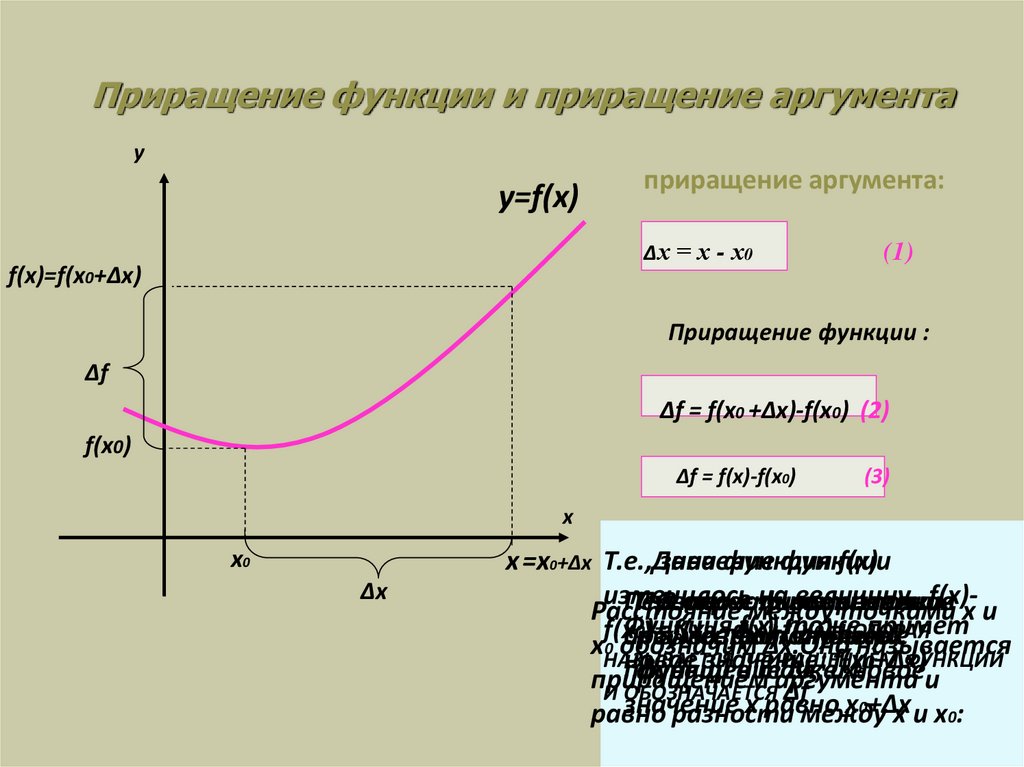
7. Приращение функции и приращение аргумента

y
y=f(x)
приращение аргумента:
∆х = х - х0
f(x)=f(x0+∆x)
(1)
Приращение функции :
∆f
∆f = f(x0 +∆x)-f(x0) (2)
f(x0)
∆f = f(x)-f(x0)
(3)
x
x0
∆x
x =x0+∆x Т.е.,Дана
значение
функция
функции
f(x)
изменилось
на
величину
f(x)Первоначальное
Пусть
В окрестности
х0-между
фиксированная
значение
точки
Расстояние
точками
хи
Функция
f(х)
тоже
примет
f(xаргумента
0точка,
)=хf(x
0 +∆x)-f(x
0),КОТОРАЯ
0 возьмём
f(х0)получило
значение
точку
х
хНАЗЫВАЕТСЯ
0 обозначим ∆х.Оно называется
ФУНКЦИИ
новое
значение:
0+∆x)
приращение
функци
вПРИРАЩЕНИЕМ
точке
∆х, иf(x
хновое
0
приращением
аргумента
и
И ОБОЗНАЧАЕТСЯ ∆f
значение
х равно
х0+∆х
равно
разности
между
х и х 0:

8.

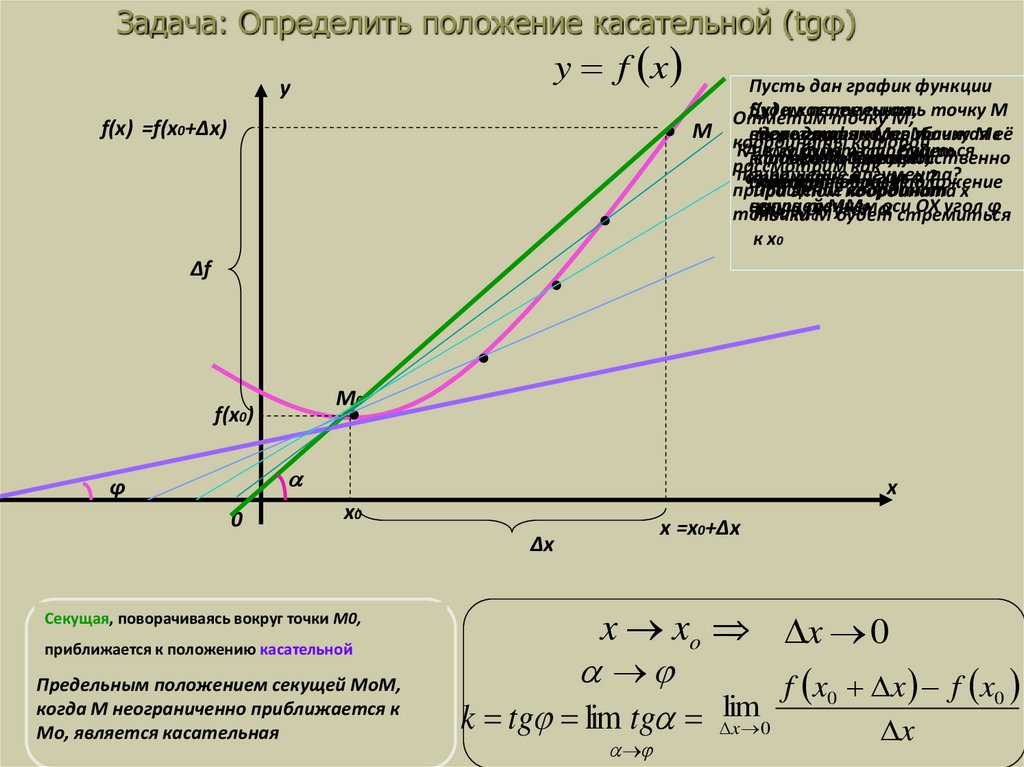
9. Задача: Определить положение касательной (tgφ)

y f x
у
f(x) =f(x0+∆x)
М
Пусть дан график функции
f(х) и касательная,
Будем
перемещать
Отметим
точку М, точку М
проходящая
через
точку
М0её
вдоль
Черезграфика,
точки
Мприближая
иМ
0
координаты
которой
КА,которая
чему
будет
стремиться
к
какому
углу
будет
с
кпроведём
точке Мобразует
0.секущую,
Соответственно
рассмотрим
как
приращение
аргумента?
стремиться
уголположение
?с
положительным
будет
меняться
которая
образует
приращение
координат
При
этом
координата
х
направлением
оси
ОХ
угол
φ
секущей
ММ
0
осьюМОХ
стремиться
точки
0М угол
точки
будет
к х0
∆f
М0
f(x0)
φ
0
х
х0
х =x0+∆x
∆x
Секущая, поворачиваясь вокруг точки М0,
приближается к положению касательной
Предельным положением секущей МоМ,
когда М неограниченно приближается к
Мо, является касательная
x xo x 0
f x0 x f x0
lim
k tg lim tg x 0
x

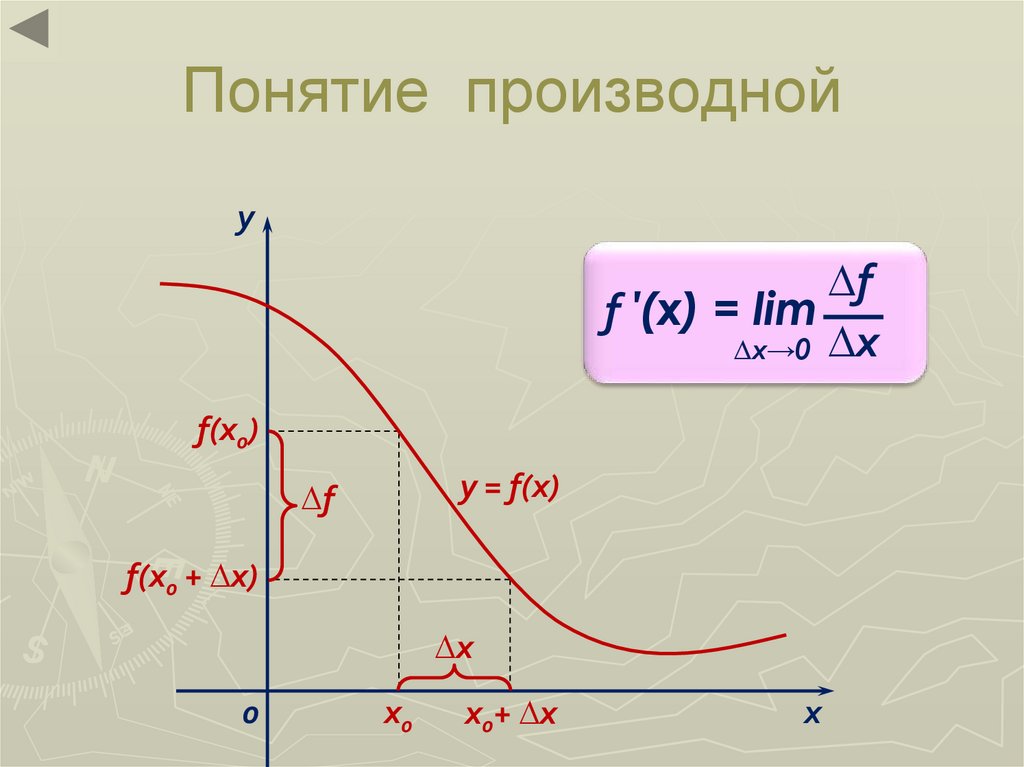
10. Понятие производной

Производной функции у = f(x), заданной на некотором
интервале (a; b), в некоторой точке х этого
интервала называют предел отношения приращения
функции в этой точке к соответствующему
приращению
аргумента,
когда
приращение
аргумента стремится к нулю.
∆f
f ′(x) = lim
∆x→0 ∆x
Нахождение производной называют дифференцированием

11. Понятие производной

у
∆f
f ′(x) = lim
∆x→0 ∆x
f(x0)
у = f(x)
∆f
f(x0 + ∆х)
∆х
0
х0
х0+ ∆х
х

12.

Алгоритм нахождения
производной
1. Зафиксировать значение х0, найти f(x0).
2. Дать аргументу х0 приращение ∆х, перейти в
новую точку х0 + ∆х, найти f(x0 + ∆х).
3. Найти приращение функции: ∆f = f(x0 + ∆х) – f(x0).
∆f
4. Составить отношение
.
∆х
∆f
5. Вычислить lim
.
∆x→0 ∆х
6. Этот предел и есть f ′(x0).

13. Примеры

1. Найти производную функции y = kx + b в точке хo
1. f x o kxo b
2. f x o Δx k x o Δx b
3. Δf f x o Δx f x o k x o Δx b kxo b
kxo k Δx b kxo b k Δx
Δf
k Δx
4.
k
Δx
Δx
Δf
5. lim
lim k k
Δx 0 Δ x
Δx 0
kx b k

14. Примеры

2. Найти производную функции y = C (C – const) в точке хo
1. f xo С
2. f x o Δx С
3. Δf f x o Δx f x o С С 0
Δf
0
4.
0
Δx Δx
Δf
5. lim
lim 0 0
Δx 0 Δ x
Δx 0
С 0

15. Примеры

3. Найти производную функции y = x2 в точке хo
1. f xo xо
2
2. f xo Δx xo Δx
2
3. Δf f x o Δx f x o x o Δx x o
2
2
x о2 2 x o Δx Δx 2 x о2 2 x o Δx Δx 2
2x o Δx Δx 2 Δx 2 x o Δx
Δf
4.
2 x o Δx
Δx
Δx
Δx
Δf
5. lim
lim 2 x o Δx 2 x o
Δx 0 Δ x
Δx 0
x 2х
2

16. Примеры

4. Найти производную функции y = √x в точке хo
1. f x o x o
2. f x o Δx x o Δx
3. Δf f x o Δx f x o x o Δx x o
x Δx x x Δx x x Δx x
2
o
o
o
o
x o Δx x o
x o Δx x o
x o Δx x o
Δf
4.
Δx Δx
o
2
o
x o Δx x o
Δx
x o Δx x o
Δx
x o Δx x o
1
x o Δx x o

17. Примеры

4. Найти производную функции y = √x в точке хo
Δf
4.
Δx Δx
Δx
x o Δx x o
1
x o Δx x o
Δf
1
1
5. lim
lim
2 x
Δx 0 Δx
Δx 0 x Δx
x
o
o
o
x
1
2 х

18. Примеры

5. Найти производную функции y = 1/x в точке хo
Δf
Δx
1
4.
2
2
Δx Δx x о x o Δx
x о x o Δx
Δf
1
1
2
5. lim
lim 2
Δx 0 Δx
Δx 0 x x Δx
xо
o
о
1
1
2
х
х

19. Таблица производных

f (x)
C
f ′(x)
0
f ′(x)
1/(2√x)
k
f (x)
√x
ex
kx + b
x2
2x
ax
ax lna
xn
nxn–1
tg x
1/cos2x
1/x
– 1/x2
ctg x
– 1/sin2x
sin x
cos x
ln x
1/x
cos x
– sin x
loga x
1/(x lna)
ex

20. Правила нахождения производной

1. Если функции u(x) и v(x) имеют в точке х
производные, то их сумма u(x) + v(x) также имеет в
этой точке производную, причем
(u + v)′ = u′ + v′
2. Если функция u(x) имеет в точке х производную и С –
данное число, то функция С∙u(x) также имеет в этой
точке производную, причем
(Сu)′ = С∙u′

21. Правила нахождения производной

3. Если функции u(x) и v(x) имеют в точке х
производные, то их произведение u(x) ∙ v(x) также
имеет в этой точке производную, причем
(u ∙ v)′ = u′∙v + u∙v′
4. Если функция v(x) имеет в точке х производную и
1
v(x) ≠ 0, то функция
также имеет в этой точке
v(x)
производную, причем
()
v′
1′
=– 2
v
v

22. Правила нахождения производной

5. Если функции u(x) и v(x) имеют в точке х
u(x)
производные и v(x) ≠ 0, то функция
также имеет
v(x)
в этой точке производную, причем
( )
u ′
u′v – uv′
v =
v2

23. Производная сложной функции

Сложная функция: y g f x .
y f 5;
Примеры: 1) y 3 x 2 x .
2
2
5
f 3 x 2 x.
2) y sin x .
y f;
f sin x.
Правило нахождения производной сложной функции
/
/
/
g f x g f f x
(производная сложной функции равна
производной основной функции
на производную внутренней функции)
Слайд №
23

24. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ

Сложная функция: y g f x .
Правило нахождения производной сложной функции
сложной функции равна
g / f x g / f f / x (производная
производной основной функции
на производную внутренней функции)
Простая
функция
Производная
простой
функции
Сложная
функция
1
f x
1
x
1
2
x
1
1
Пример:
1) y
. y ;
f
sin x
f / sin x.
Производная сложной функции
/
f
x
1
/
2
f x 2
f x
f x
1
1
cos x
/
1
№ sin x 2 cos x 242 .
y
sin 2Слайд
x
sin x
sin x
sin x
/

25. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ

Сложная функция:y g f x .
Правило нахождения производной сложной функции
сложной функции равна
g / f x g / f f / x (производная
производной основной функции
на производную внутренней функции)
Простая
функция
x
Пример:
Производная
простой
функции
Сложная
функция
1
f x
2 x
Производная сложной функции
1
2 f x
f / x
f / x
2 f x
1) y 2 x 3 x . y f ;
f 2 x 3 x.
1) y 2 x x .
3
1
2 2x x
3
2 x 1
3
Слайд №
/
6x2
2x 2x 1
2
3x
2 x2 1
.
25

26. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ

Сложная функция:y g f x .
Правило нахождения производной сложной функции
сложной функции равна
g / f x g / f f / x (производная
производной основной функции
на производную внутренней функции)
Простая
функция
Производная
простой
функции
Сложная
функция
Производная сложной
функции
sin x
cos x
sin f x
cos f x f / x
Пример:
1) y sin 2 x .
3
y sin f ;
f 2x .
3 /
y sin 2 x cos 2 x 2 x 2 cos 2 x .
3
3
3
3
/
/
Слайд №
26

27. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ

Простая
функция
Производная
простой
функции
Сложная
функция
Производная сложной функции
n
nx n 1
f n x
n f n 1 x f / x
1
x
1
2
x
1
f x
x
2 x
f x
sin x
cos x
sin f x
cos f x f / x
cos x
sin x
cos f x
sin f x f / x
tgx
1
2
cos x
tgf x
/
f
x
1
/
f x
2
cos f x
cos 2 f x 27
x
1
Слайд №
f / x
2
f x
f / x
2 f x

28. Закрепление изученного материала.

Вычислите производные:
4
у
(
x
3
)
1)
2) у ( х 3 х 2 11)3
3) у sin( 5 x 3)
4) у cos10 x
5) у tg 4 x
6)
Слайд №
у х2 1
28

29.

у ( 2 3 х)8
у 5х 2 3
у (2 х 3) 4
Слайд №
29