Похожие презентации:
Понятие производной
1.
Понятиепроизводной.
Урок лекция на 2
часа.
2.
Содержание1. Приращение функции
2. Геометрический смысл приращения
функции
3. Понятие производной.
4. Алгоритм нахождения производной.
5. Примеры.
6. Таблица производных.
3. Приращение функции
4.
Дан график функции у=4-х2По графику найти значение
функции в точке х1=1 и
х2=2
у
4
Разность х2 - х1=2-1=1; ∆x=1
f (1)=3; f(2)=0; f(2)- f(1)=0-3= -3
∆f=-3
3
2
∆f
1
-2
-1
0
1
2
∆x
х
5.
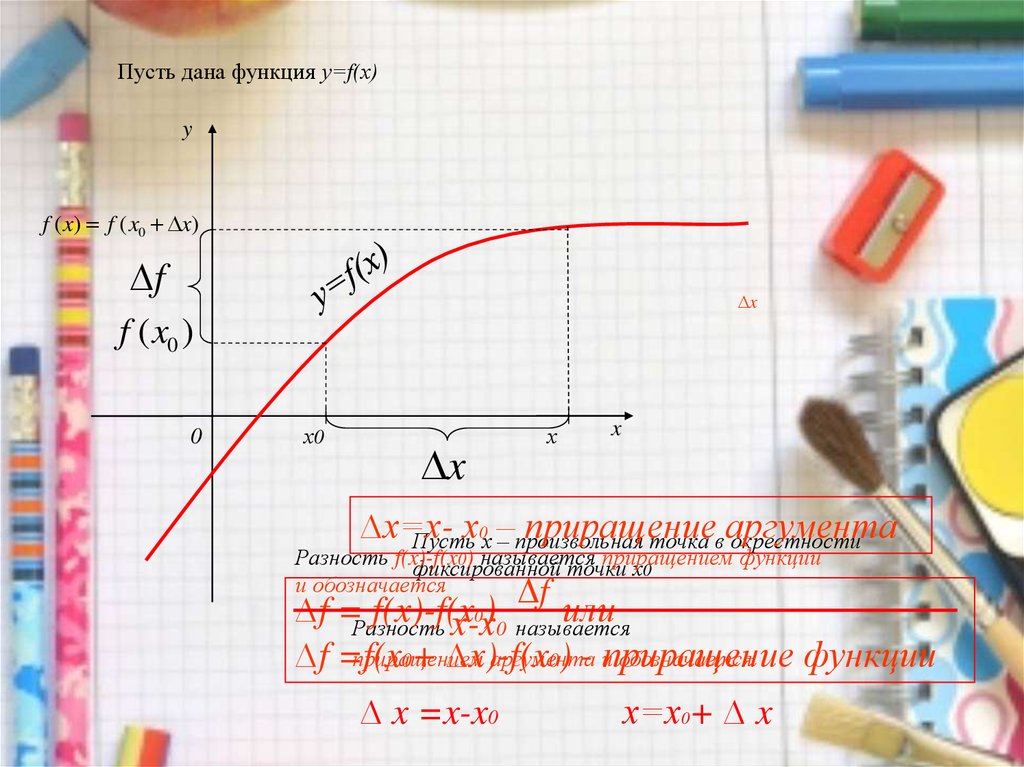
Пусть дана функция у=f(х)y
f ( x) f ( x0 x)
f
x
f ( x0 )
0
х0
x
х
x
∆х=хх0х –– произвольная
приращение
Пусть
точка в аргумента
окрестности
Разность f(x)-f(x
0) называется приращением функции
фиксированной
точки х0
и обозначается
f
∆f =Разность
f(x)-f(x
0)
или
х-х
0 называется
приращением
аргумента
обозначается
∆f =f(x
0+ ∆x)-f(x
0) - и
приращение
функции
∆ x =x-x0
х=х0+ ∆ x
6.
СодержаниеПример 1:
Найти приращение аргумента и приращение
2
функции в точке х0, если
f ( x) x
x 1,9
x0 2
Решение:
x x x0 ;
x 1,9 2 0,1;
f f ( x) f ( x0 );
f f (1,9) f (2) 1,9 2 3,61 4 0,39
2
2
Ответ : x 0,1; f 0, 39
7. Геометрический смысл приращения функции
y=kх+by
В
f ( x) f ( x0 x)
f
А
f ( x0 )
0
f
k tg
x
х0
f
С
x
x
х
k tg
ABC - прямоугольный
x
BC
tg
AC
Прямая l , проходящая через
любые две точки графика функции,
называется секущей к графику функции.
-угловой коэффициент
секущей к графику
функции
8.
Содержание№184(а )
Пример
f ( x)
Решение :
1 2
x ; x0 0; x 1
2
tg
x x x0 ;
f f ( x) f ( x0 );
x 1 0 1;
1
k tg
2
f
;
x
1 2 1 2 1
f f (1) f (0) 1 0
2
2
2
0 острый
1
Ответ : tg ; острый
2
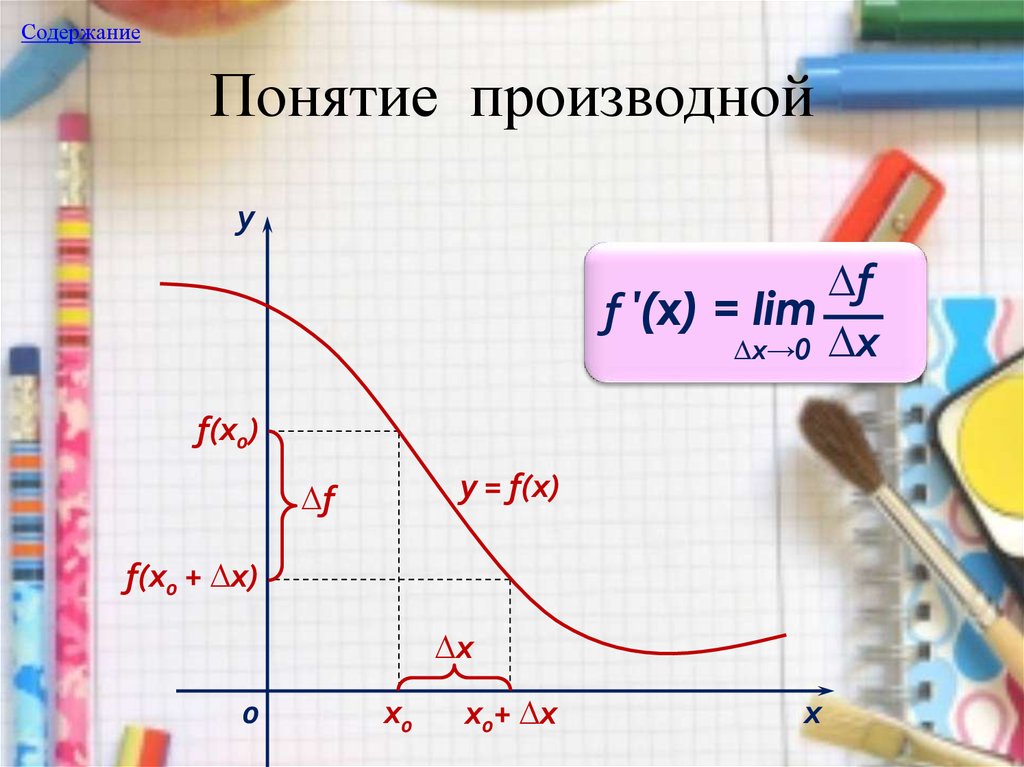
9. Понятие производной
Производной функции у = f(x), заданной на некотороминтервале (a; b), в некоторой точке х этого
интервала называют предел отношения приращения
функции в этой точке к соответствующему
приращению
аргумента,
когда
приращение
аргумента стремится к нулю.
∆f
f ′(x) = lim
∆x→0 ∆x
Нахождение производной называют дифференцированием
10. Понятие производной
СодержаниеПонятие производной
у
∆f
f ′(x) = lim
∆x→0 ∆x
f(x0)
у = f(x)
∆f
f(x0 + ∆х)
∆х
0
х0
х0+ ∆х
х
11.
СодержаниеАлгоритм нахождения
производной
1. Зафиксировать значение х0, найти f(x0).
2. Дать аргументу х0 приращение ∆х, перейти в
новую точку х0 + ∆х, найти f(x0 + ∆х).
3. Найти приращение функции: ∆f = f(x0 + ∆х) – f(x0).
∆f
4. Составить отношение
.
∆х
∆f
5. Вычислить lim
.
∆x→0 ∆х
6. Этот предел и есть f ′(x0).
12. Примеры
СодержаниеПримеры
1. Найти производную функции y = kx + b в точке хo
1. f xo kxo b
2. f xo Δx k xo Δx b
3. Δf f x o Δx f x o k x o Δx b kxo b
kxo k Δx b kxo b k Δx
Δf
k Δx
4.
k
Δx
Δx
Δf
5. lim
lim k k
Δx 0 Δx
Δx 0
kx b
k
13. Примеры
СодержаниеПримеры
2. Найти производную функции y = C (C – const) в точке хo
1. f xo С
2. f xo Δx С
3. Δf f xo Δx f xo С С 0
Δf
0
4.
0
Δx Δx
Δf
5. lim
lim 0 0
Δx 0 Δ x
Δx 0
С 0
14. Примеры
СодержаниеПримеры
3. Найти производную функции y = x2 в точке хo
1. f xo xо
2
2. f xo Δx xo Δx
2
3. Δf f x o Δx f x o x o Δx x o
2
2
x о2 2 x o Δx Δx 2 x о2 2 x o Δx Δx 2
2x o Δx Δx 2 Δx 2 x o Δx
Δf
4.
2 x o Δx
Δx
Δx
Δx
Δf
5. lim
lim 2 x o Δx 2 x o
Δx 0 Δ x
Δx 0
x 2х
2
15. Примеры
СодержаниеПримеры
4. Найти производную функции y = √x в точке хo
1. f x o x o
2. f xo Δx xo Δx
3. Δf f xo Δx f x o x o Δx x o
x o Δx x o
x o Δx x o
x o Δx x o
x o Δx x o
x o Δx x o
Δf
4.
Δx Δx
x o Δx
x
2
o
x o Δx x o
Δx
x o Δx x o
Δx
x o Δx x o
2
1
x o Δx x o
16. Примеры
СодержаниеПримеры
4. Найти производную функции y = √x в точке хo
Δf
4.
Δx Δx
Δx
x o Δx x o
1
x o Δx x o
Δf
1
1
5. lim
lim
2 x
Δx 0 Δx
Δx 0 x Δx
x
o
o
o
x
1
2 х
17. Примеры
СодержаниеПримеры
5. Найти производную функции y = 1/x в точке хo
1
1. f x o
xо
1
2. f x o Δx
x o Δx
1
1
3. Δf f x o Δx f x o
x o Δx x o
x o x o Δx
Δx
2
x o x o Δx
x о x o Δx
Δf
Δx
1
4.
2
2
Δx Δx x о x o Δx
x о x o Δx
18. Примеры
СодержаниеПримеры
5. Найти производную функции y = 1/x в точке хo
Δf
Δx
1
4.
2
2
Δx Δx x о x o Δx
x о x o Δx
Δf
1
1
2
5. lim
lim 2
Δx 0 Δx
Δx 0 x x Δx
xо
o
о
1
1
2
х
х
19. Таблица производных
СодержаниеТаблица производных
f (x)
C
f ′(x)
0
f (x)
√x
f ′(x)
1/(2√x)
kx + b
k
ex
ex
x2
2x
ax
ax lna
xn
nxn–1
tg x
1/cos2x
1/x
– 1/x2
ctg x
– 1/sin2x
sin x
cos x
ln x
1/x
cos x
– sin x
loga x
1/(x lna)



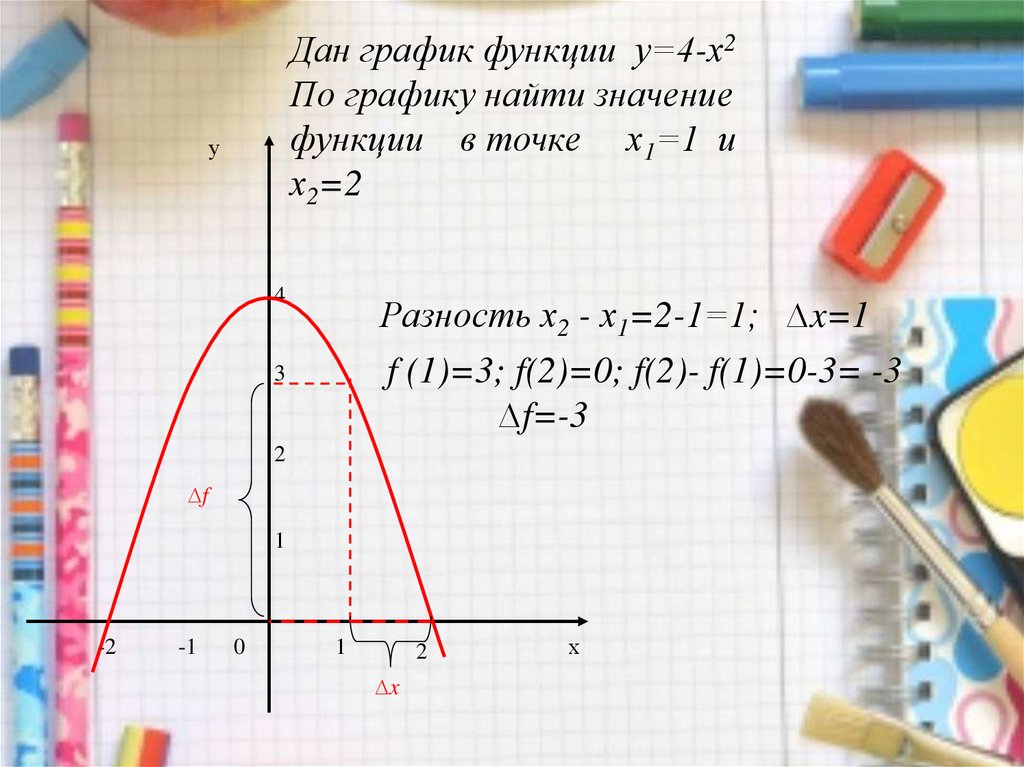













 Математика
Математика








