Задачи, приводящие к понятию производной

1. Задачи, приводящие к понятию производной.

10
9
8
7
6
5
4
3
2
1
0
Y
X
1
2
3
4
5
6
7
8
9
10

2. В начале было слово.

► К понятию производной можно
прийти, рассматривая, например,
такое широко используемое в
физике понятие, как мгновенная
скорость неравномерно
движущегося тела.
► Мы познакомились с этим
понятием, изучая в курсе физики
раздел кинематики, а точнее
кинематики прямолинейного
неравномерного движения.

3.

► Совершенно верно. Как же Вы
представляете себе мгновенную
скорость? Что это такое?
► Мгновенной скоростью тела
называют скорость, которую оно
имеет в данный момент времени (в
данной точке траектории)

4.

А как Вы представляете себе
мгновенную скорость?
Так и представляю… Если тело
движется равномерно, то в разные
моменты времени его скорость
одинакова. Если тело движется
неравномерно (ускоряясь или
замедляясь, то в разные моменты
времени его скорость будет, вообще
говоря, различной

5.

Разве Вы не чувствуете, что фраза
«скорость в данный момент времени» не
более как синоним фразы «мгновенная
скорость»? Как говорится, «что в лоб, что
по лбу». Термин «скорость в данный
момент времени нуждается в разъяснении
в той же мере, в какой нуждается в нём
термин «мгновенная скорость».
► Физик эту проблему решает просто. У
него есть приборы, например, спидометр.
А математик создаст математическую
модель процесса.
Итак, проблема поставлена. Приступим к её
решению.

6.

Остановись мгновенье –
мы тебя исследуем !
Сначала мы определили «территорию» своих
исследований. В каких ещё науках математика поможет
решить подобную проблему.
Оказалось, что связь между количественными
характеристиками самых различных процессов,
исследуемых физикой, химией, биологией, экономикой,
техническими науками, аналогична связи между путём и
скоростью.
Основным математическим понятием, выражающим
эту связь является производная.

7. Производная

Центральные понятия дифференциального исчисления
– производная и дифференциал возникли при
рассмотрении большого числа задач естествознания и
математики, приводивших к вычислению пределов
одного и того же типа. Важнейшие среди них –
физическая задача определения скорости
неравномерного движения и геометрическая задача
построения касательной к кривой.
Рассмотрим подробно каждую из них.

8.

Будем вслед за итальянским учёным
Г.Галилеем изучать закон
свободного падения тел. Поднимем
камешек и затем из состояния покоя
отпустим его. Движение свободно
падающего тела явно
неравномерное. Скорость v
постепенно возрастает. Но как
именно выглядит зависимость v(t) ?

9.

Фиксируем момент t, в который мы хотим знать значение
скорости v(t). Пусть h – небольшой промежуток времени,
прошедший от момента t. За это время падающее тело пройдёт
путь, равный s(t+h)-s(t).
Если промежуток времени h очень мал, то приближённо
s(t+h)-s(t)≈v(t)∙h, или s (t h) s (t ) v (t ) , причём
h
последнее приближённое равенство тем точнее, чем меньше h.
Значит величину v(t) скорости в момент t можно
рассматривать как предел, к которому стремится отношение,
выражающее среднюю скорость на интервале времени от
момента t до момента t+h.
Сказанное записывают в виде
s (t h) s (t )
v(t ) lim
h 0
h

10. Задача о мгновенной скорости

► Предел средней скорости за
промежуток времени от t0 до t при
t→ t0, называется мгновенной
скоростью v(t0) в момент времени t0
v(t0) =
S (t ) S (t0 )
f ( x) f ( x0 )
lim vср (t0 ; t ) lim
lim
t t 0
t t 0
x x0
t t0
x x0

11. А л г о р и т м

Алгоритм
∆t = t – t0
2) ∆v = v(t+t0) - v(t0)
∆x = x – x0
∆f = f(x+x0) – f(x0)
3)
. v v(t0 t ) v(t0 )
t
t t0
f ( x0 x) f ( x0 )
f
x
x x0
1)
S
4) v
. (t0 ) S lim
t 0 t
f
f ( x0 ) lim
x 0 x

12.

Рассмотрим теперь другой классический пример,
который решается в терминах производной, построение касательной к кривой. Требуется построить
прямую Т, касательную в т. А к кривой – графику
функции y = f(x).

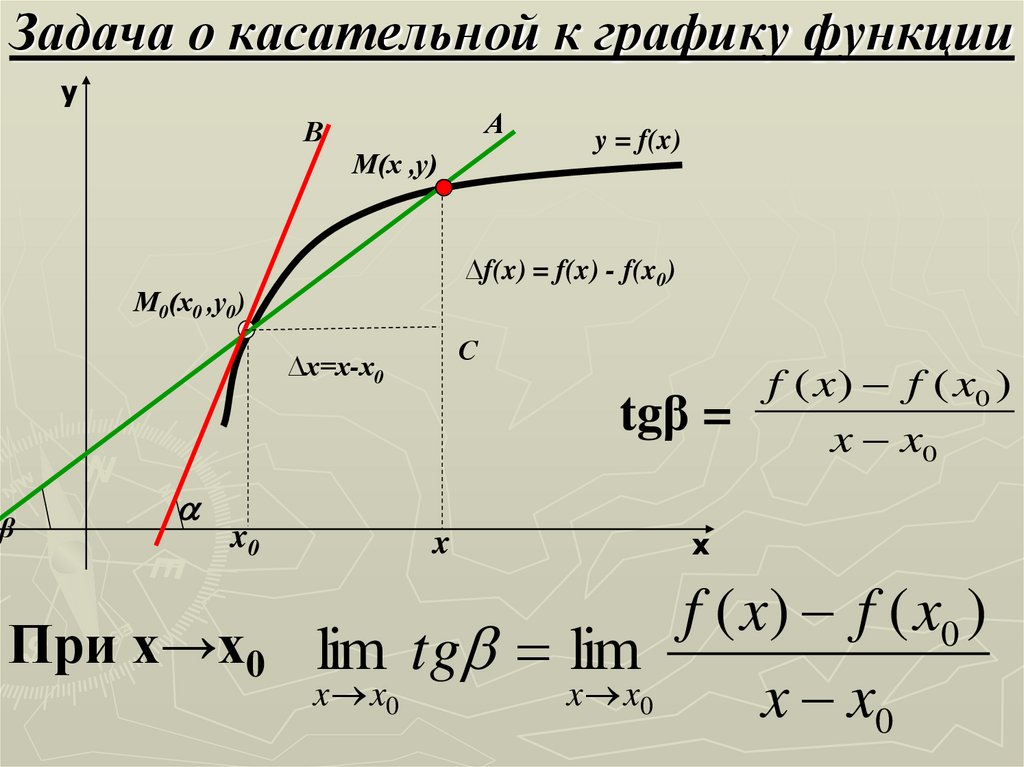
13. Задача о касательной к графику функции

y
А
В
М(х ,у)
y = f(x)
∆f(x) = f(x) - f(x0)
М0(х0 ,у0)
С
∆х=х-х0
tgβ =
β
x0
При х→х0
x
f ( x) f ( x0 )
x x0
x
f ( x) f ( x0 )
lim tg lim
x x0
x x0
x x0

14. А л г о р и т м

Алгоритм
1)
2)
3)
4)
∆x = x – x0
∆f = f(x+x0) – f(x0)
f ( x0 x ) f ( x0 )
f
x
x x0
f
f ( x0 ) lim
x 0 x

15.

Задача о скорости химической реакции
Средняя скорость растворения соли в воде за
промежуток времени [t0;t1] (масса соли,
растворившейся в воде изменяется по закону
х = f(t)) определяется по формуле
х f (t1 ) f (t0 )
vср
t
t1 вtданный
0
Скорость растворения
момент времени
v(t0 ) f (t0 )
.

16. А л г о р и т м

Алгоритм
1)
∆t = t – t0
2) ∆f = f(t1) - f(t0)
∆x = x – x0
∆f = f(x) – f(x0)
f (t1 ) f (t0 )
f
3) .
t
t t0
f
4) v. (t0 ) f (t0 ) lim
t 0 t
f ( x1 ) f ( x0 )
f
x
x x0
f
f ( x0 ) lim
x 0 x

17.

1
y
y =f(x)
A
D
M0
C
x
O
B
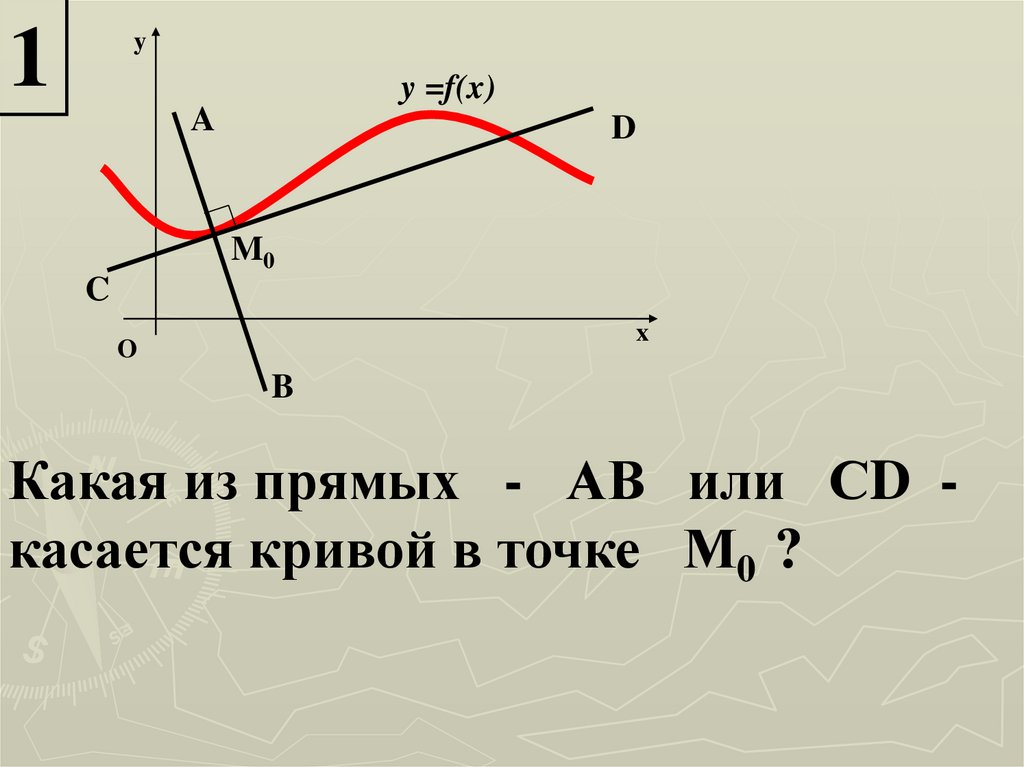
Какая из прямых - АВ или СD касается кривой в точке М0 ?

18.

2 Следует ли считать
понятия «прямая
касается кривой» и
«прямая пересекает
кривую»
взаимоисключающими ?

19.

3
y
А 0
В
С
D E
F
x
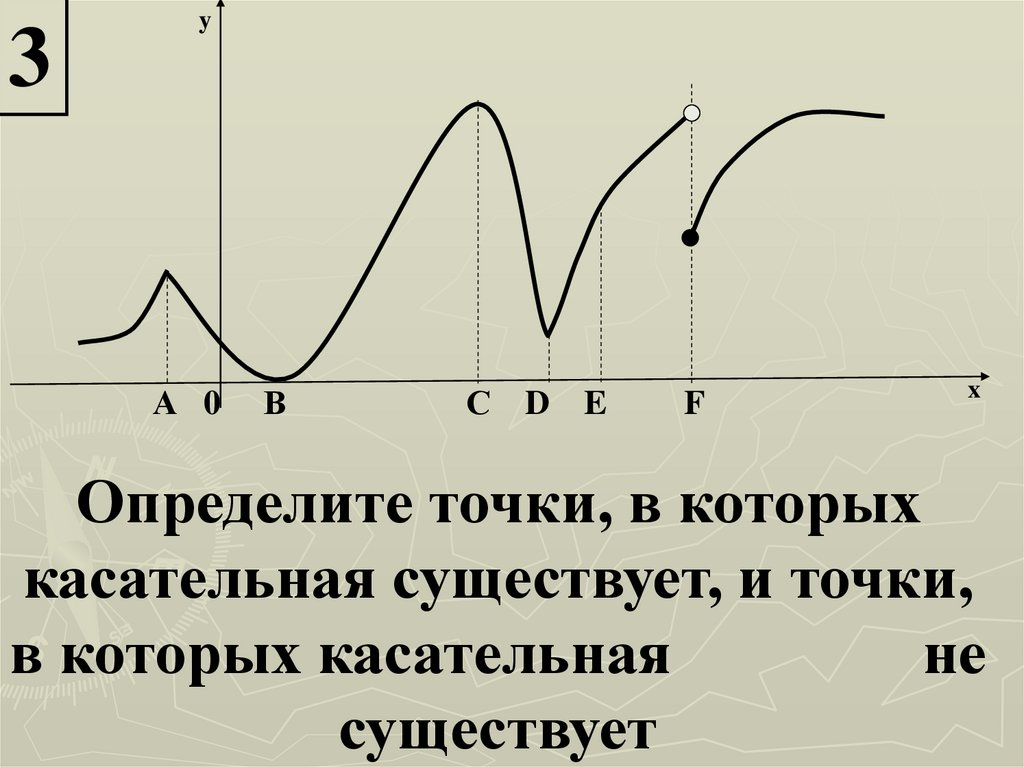
Определите точки, в которых
касательная существует, и точки,
в которых касательная
не
существует

20.

4
y
M
y=f(x)
∆y
M0
T
∆x
0
x0
x0+∆x
x
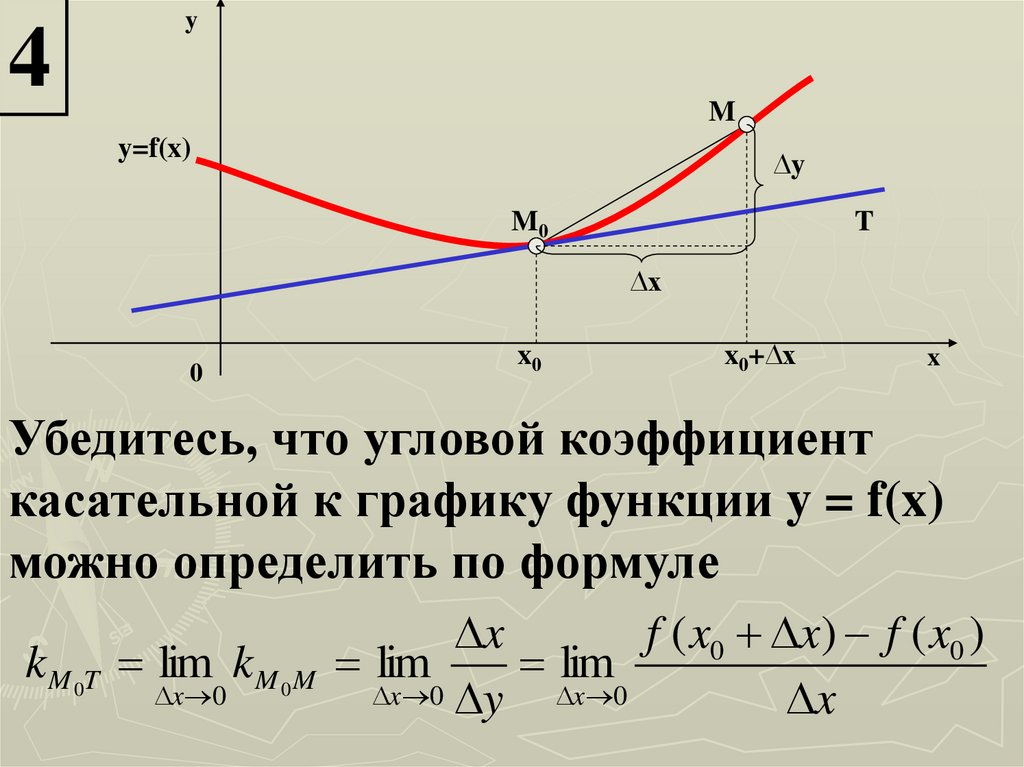
Убедитесь, что угловой коэффициент
касательной к графику функции y = f(x)
можно определить по формуле
f ( x0 x) f ( x0 )
x
k M 0T lim k M 0 M lim
lim
x 0
x 0 y
x 0
x

21.

5
►Найдите угловой коэффициент
касательной к параболе у = х2 :
►а) в точке (1;1);
2
►б) в точке (х0 ; х 0 ).
►Используя полученный результат,
найдите способ построения
касательной в любой точке
параболы.

22.

6
►Найдите угловой коэффициент
касательной к кривой у = х3 в точках
3
(х0 ; х 0 ); (1 ; 1); (0 ; 0).
►Как построить касательную к кривой
у = х3 в любой её точке ? Какая
прямая является касательной в токе
(0 ; 0) ?