Похожие презентации:
Производная. Задачи, приводящие к понятию производной
1.
Производная
2.
Содержание1. Задачи, приводящие к понятию производной
2. Понятие производной.
3. Алгоритм нахождения производной.
4. Примеры.
5. Таблица производных.
6. Физический смысл производной.
7. Геометрический смысл производной
8. Правила нахождения производных.
9. Непрерывность функции.
3. Задачи, приводящие к понятию производной
Задача 1 (о скорости движения)По прямой, на которой заданы начало отсчета,
единица измерения (метр) и направление,
движется некоторое тело (материальная точка).
Закон движения задан формулой s=s (t), где t —
время (в секундах), s (t) — положение тела на
прямой (координата движущейся материальной
точки) в момент времени t по отношению к
началу отсчета (в метрах).
Найти скорость движения тела в момент времени
t (в м/с).
4. Задачи, приводящие к понятию производной
ОМ
N
Предположим, что в начальный момент времени t тело
находилось в точке M, её координата – s(t).
за время t оно прошло путь МN .
Координата точки N – s(t+ t).
Тогда МN = s = s(t+ t) – s(t)
Нетрудно найти среднюю скорость движения тела за
промежуток времени [t; t+∆t] :
s
vср
t
5.
Задачи, приводящие к понятию производнойА что такое скорость v (t) в момент времени t (её
называют иногда мгновенной скоростью)?
Можно сказать так: это средняя скорость
движения за промежуток времени [t; t+∆t]
при условии , что ∆t выбирается все меньше и
меньше;
иными словами, при условии, что ∆t→0.
Это значит , что
v t lim vср
t 0
s
v(t ) lim
t
t 0
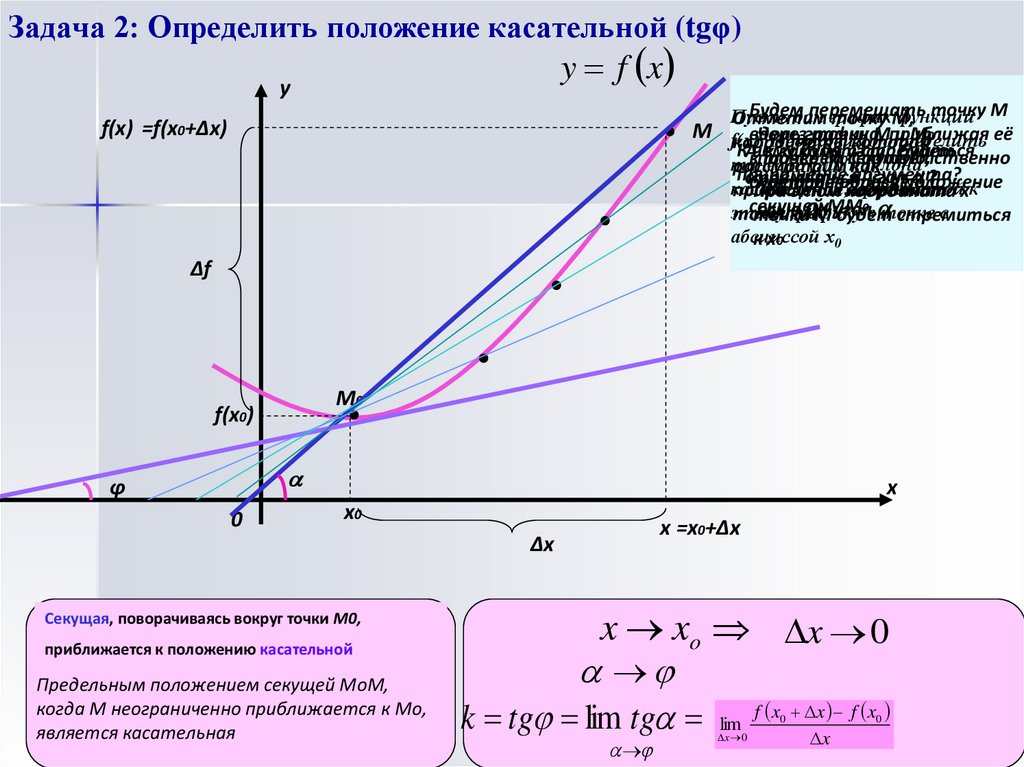
6. Задача 2: Определить положение касательной (tgφ)
y f xу
Будем
перемещать
точку М
Пусть
дан
график
функции
Отметим
точку М,
М f(x).
вдоль
графика,
приближая
её
Через
точки
Мопределить
и М0
Необходимо
координаты
которой
КАкчему
будет
стремиться
к
какому
углу
будет
точке
М0.секущую,
Соответственно
проведём
тангенс
угла
наклона
рассмотрим
как
приращение
аргумента?
стремиться
уголположение
?с
будет
меняться
которая
образует
касательной,
проведённой
приращение
координат
При
этом
координата
хк
секущей
ММ
0
осью
этому
графику
в точке
с
точки
МОХ
0М угол
точки
будет
стремиться
абсциссой
х0
к х0
f(x) =f(x0+∆x)
∆f
М0
f(x0)
φ
0
х
х0
х =x0+∆x
∆x
Секущая, поворачиваясь вокруг точки М0,
приближается к положению касательной
Предельным положением секущей МоМ,
когда М неограниченно приближается к Мо,
является касательная
x xo x 0
k tg lim tg lim f x xx f x
0
x 0
0
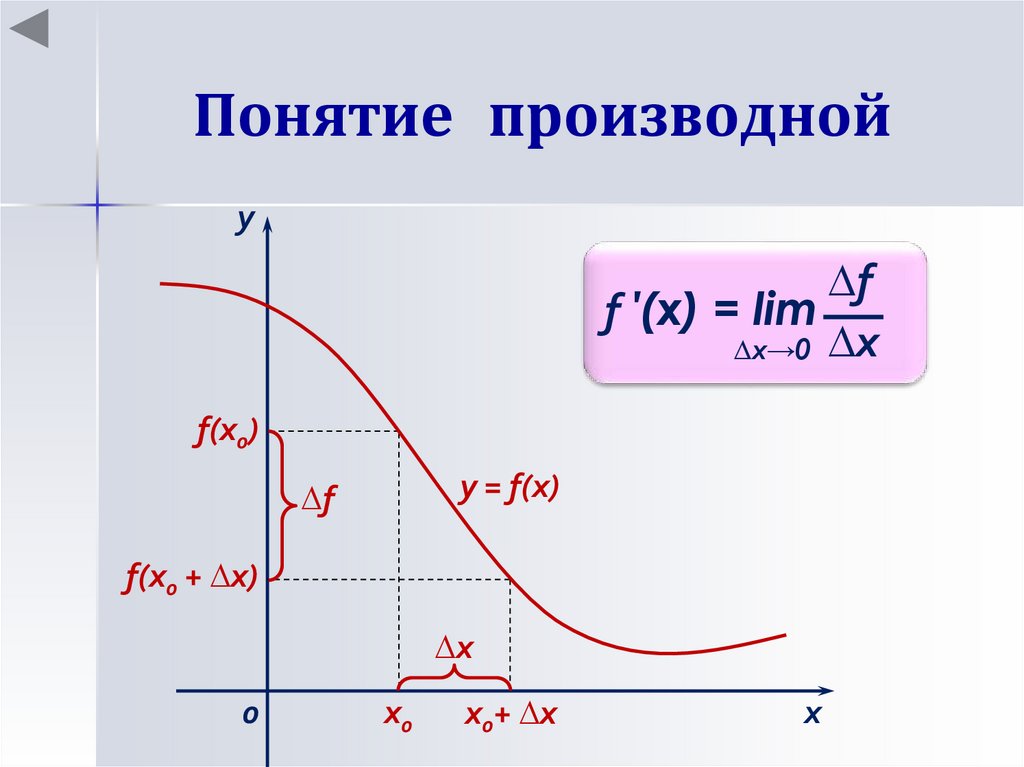
7. Понятие производной
Производной функции у = f(x), заданной на некотороминтервале (a; b), в некоторой точке х этого интервала
называют предел отношения приращения функции в
этой точке к соответствующему приращению
аргумента, когда приращение аргумента стремится к
нулю.
∆f
f ′(x) = lim
∆x→0 ∆x
Нахождение производной называют дифференцированием
8. Понятие производной
у∆f
f ′(x) = lim
∆x→0 ∆x
f(x0)
у = f(x)
∆f
f(x0 + ∆х)
∆х
0
х0
х0+ ∆х
х
9.
Алгоритм нахожденияпроизводной
1. Зафиксировать значение х0, найти f(x0).
2. Дать аргументу х0 приращение ∆х, перейти в
новую точку х0 + ∆х, найти f(x0 + ∆х).
3. Найти приращение функции: ∆f = f(x0 + ∆х) – f(x0).
∆f
4. Составить отношение
.
∆х
∆f
5. Вычислить lim
.
∆x→0 ∆х
6. Этот предел и есть f ′(x0).
10. Примеры
1. Найти производную функции y = kx + b в точке хo1. f x o kxo b
2. f x o Δx k x o Δx b
3. Δf f x o Δx f x o k x o Δx b kxo b
kxo k Δx b kxo b k Δx
Δf
k Δx
4.
k
Δx
Δx
Δf
5. lim
lim k k
Δx 0 Δ x
Δx 0
kx b k
11. Примеры
2. Найти производную функции y = C (C – const) в точке хo1. f xo С
2. f x o Δx С
3. Δf f x o Δx f x o С С 0
Δf
0
4.
0
Δx Δx
Δf
5. lim
lim 0 0
Δx 0 Δ x
Δx 0
С 0
12. Примеры
3. Найти производную функции y = x2 в точке хo1. f xo xо
2
2. f xo Δx xo Δx
2
3. Δf f x o Δx f x o x o Δx x o
2
2
x о2 2 x o Δx Δx 2 x о2 2 x o Δx Δx 2
2x o Δx Δx 2 Δx 2 x o Δx
Δf
4.
2 x o Δx
Δx
Δx
Δx
Δf
5. lim
lim 2 x o Δx 2 x o
Δx 0 Δ x
Δx 0
x 2х
2
13. Примеры
4. Найти производную функции y = √x в точке хo1. f x o x o
2. f x o Δx x o Δx
3. Δf f x o Δx f x o x o Δx x o
x Δx x x Δx x x Δx x
2
o
o
o
o
x o Δx x o
x o Δx x o
x o Δx x o
Δf
4.
Δx Δx
o
2
o
x o Δx x o
Δx
x o Δx x o
Δx
x o Δx x o
1
x o Δx x o
14. Примеры
4. Найти производную функции y = √x в точке хoΔf
4.
Δx Δx
Δx
x o Δx x o
1
x o Δx x o
Δf
1
1
5. lim
lim
2 x
Δx 0 Δx
Δx 0 x Δx
x
o
o
o
x
1
2 х
15. Примеры
5. Найти производную функции y = 1/x в точке хo1
1. f x o
xо
1
2. f x o Δx
x o Δx
1
1
3. Δf f x o Δx f x o
x o Δx x o
x o x o Δx
Δx
2
x o x o Δx
x о x o Δx
Δf
Δx
1
4.
2
2
Δx Δx x о x o Δx
x о x o Δx
16. Примеры
5. Найти производную функции y = 1/x в точке хoΔf
Δx
1
4.
2
2
Δx Δx x о x o Δx
x о x o Δx
Δf
1
1
2
5. lim
lim 2
Δx 0 Δx
Δx 0 x x Δx
xо
o
о
1
1
2
х
х
17. Таблица производных
f (x)f ′(x)
C
0
kx + b
k
x2
2x
xn
nxn–1
1
x
1
2
x
18. Таблица производных
f (x)f ′(x)
х
1
2 x
sin x
cos x
cos x
ex
– sin x
ex
ax
ax lna
19. Таблица производных
f (x)f ′(x)
tg x
1
2
cos x
1
2
sin x
1
x
1
x ln a
ctg x
ln x
loga x
20. Физический ( механический ) смысл производной
Если при прямолинейном движении путь s,пройденный точкой, есть функция от времени t,
т.е. s = s(t), то скорость точки есть производная
от пути по времени, т.е. v(t) = s′(t).
Производная выражает мгновенную скорость в
момент времени t.
21.
Геометрический смысл производнойПроизводная функции в данной точке численно равна тангенсу
угла наклона касательной, проведенной к графику через эту
точку, к положительному направлению оси ОХ.
22. Правила нахождения производной
1. Если функции u(x) и v(x) имеют в точке хпроизводные, то их сумма u(x) + v(x) также имеет в
этой точке производную, причем
(u + v)′ = u′ + v′
2. Если функция u(x) имеет в точке х производную и С –
данное число, то функция С∙u(x) также имеет в этой
точке производную, причем
(Сu)′ = С∙u′
23. Правила нахождения производной
3. Если функции u(x) и v(x) имеют в точке хпроизводные, то их произведение u(x) ∙ v(x) также
имеет в этой точке производную, причем
(u ∙ v)′ = u′∙v + u∙v′
4. Если функция v(x) имеет в точке х производную и
1
v(x) ≠ 0, то функция
также имеет в этой точке
v(x)
производную, причем
()
v′
1′
=– 2
v
v
24. Правила нахождения производной
5. Если функции u(x) и v(x) имеют в точке хu(x)
производные и v(x) ≠ 0, то функция
также имеет
v(x)
в этой точке производную, причем
( )
u ′
u′v – uv′
v =
v2
25. Производная сложной функции
(f(g(x)))′ = f′(g(x))∙g′(x)Примеры:
1. ((5x – 3)3)′ = 3(5x – 3)2∙(5x – 3)′ =
= 3(5x – 3)2 ∙ 5 = 15(5x – 3)2
2. (sin(4x + 8))′ = cos(4x + 8)∙(4x + 8)′ =
= cos(4x + 8)∙4 = 4 cos(4x + 8)
26.
Если функция имеет производную (дифференцируема)в точке х, то она непрерывна в этой точке.
























 Математика
Математика








