Теорема Менелая при решении задач ОГЭ и ЕГЭ (Мастер-класс)

1.

Теорема Менелая при
решении задач ОГЭ и ЕГЭ
(Мастер-класс)
Учитель математики и физики
МБОУ «Бурнашевская СОШ»
Зарифуллина Милауша Галимхановна
Август, 2019 год

2.

Цель работы – изучить теорему Менелая
и рассмотреть ее применение
к решению планиметрических задач.
Задача работы - выявление эффективности
применения теоремы Менелая по
сравнению с другими способами решения
планиметрических задач.

3.

Менела́й Александри́йский (ок. 100 н. э.) —
древнегреческий математик и астроном. Время
его жизни и деятельности определяется
приведёнными в «Алмагесте» Птолемея двумя
астрономическими наблюдениями, которые
Менелай произвёл в Риме в первом году
царствования Трояна, то есть в 98 году н. э..
Главное сочинение Меналая — «Сферика» в трёх
книгах. Его греческий оригинал утрачен, и
содержание его известно по арабским, а также
последующим вторичным латинским и еврейским
переводам.

4.

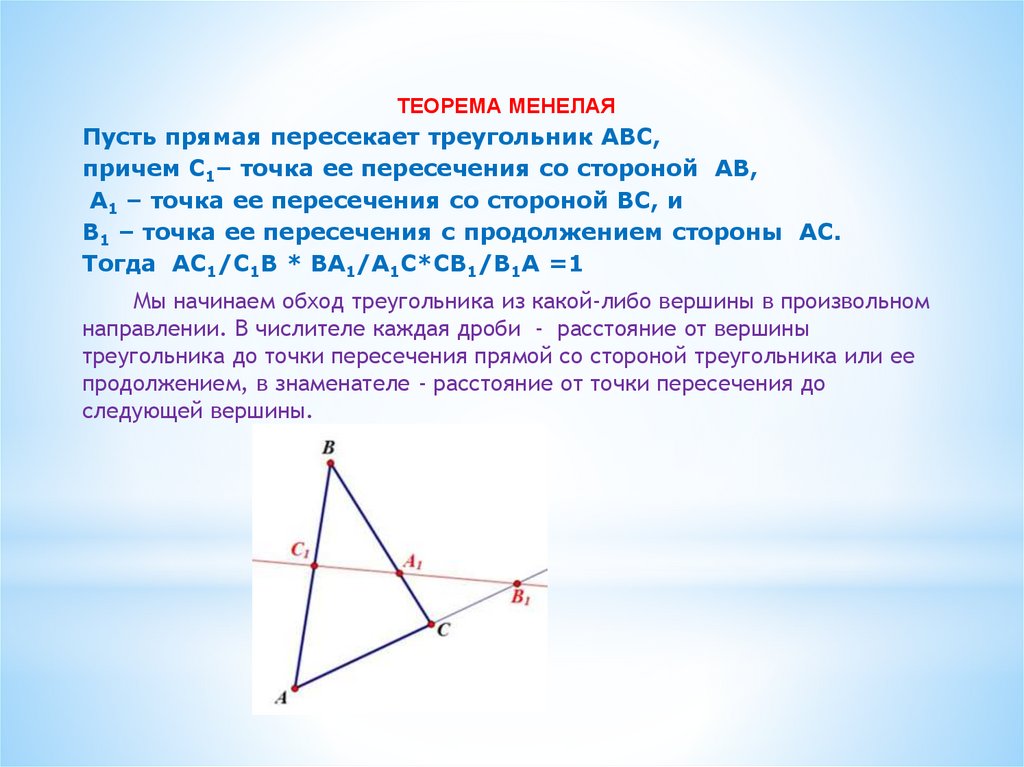
ТЕОРЕМА МЕНЕЛАЯ
Пусть прямая пересекает треугольник ABC,
причем С1– точка ее пересечения со стороной AB,
А1 – точка ее пересечения со стороной BC, и
В1 – точка ее пересечения с продолжением стороны AC.
Тогда АС1/С1В * ВА1/А1С*СВ1/В1А =1
Мы начинаем обход треугольника из какой-либо вершины в произвольном
направлении. В числителе каждая дроби - расстояние от вершины
треугольника до точки пересечения прямой со стороной треугольника или ее
продолжением, в знаменателе - расстояние от точки пересечения до
следующей вершины.

5.

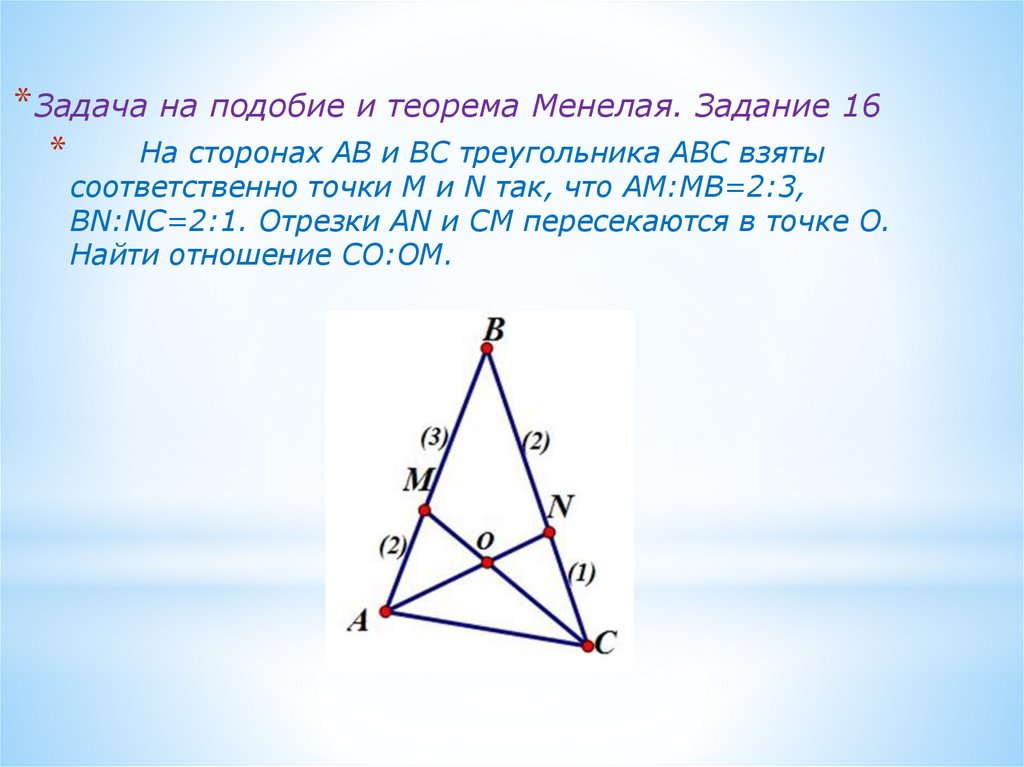
* Задача на подобие и теорема Менелая. Задание 16
*
На сторонах AB и BC треугольника ABC взяты
соответственно точки M и N так, что AM:MB=2:3,
BN:NC=2:1. Отрезки AN и CM пересекаются в точке O.
Найти отношение CO:OM.

6.

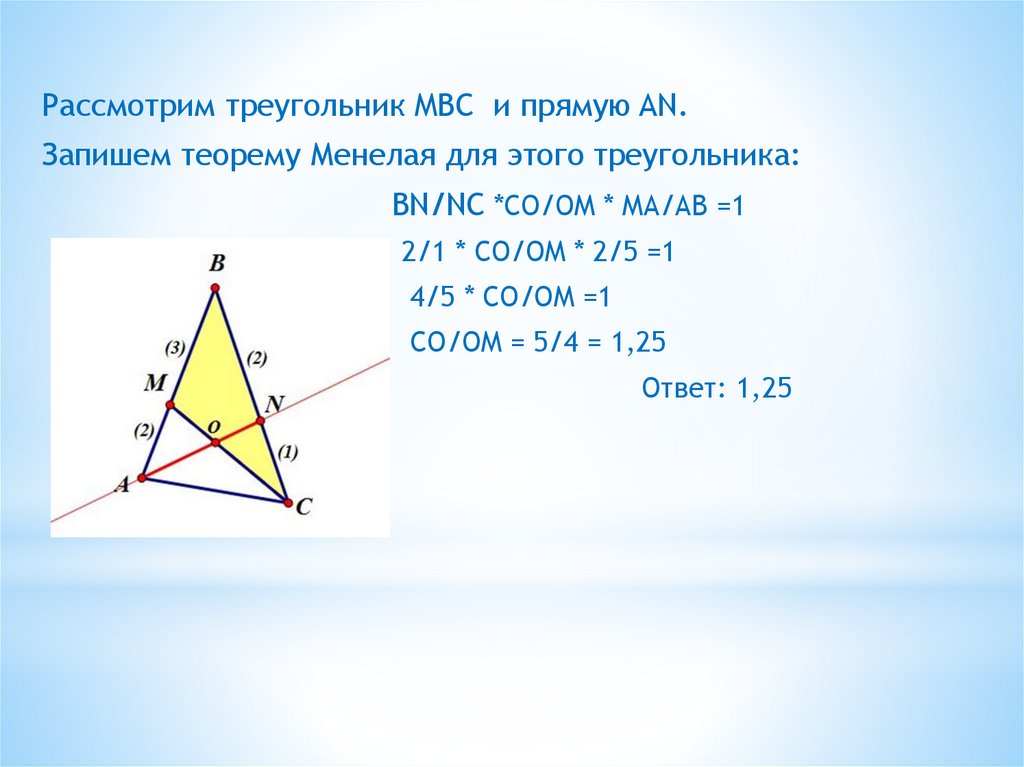
Рассмотрим треугольник MBC и прямую AN.
Запишем теорему Менелая для этого треугольника:
BN/NC *CO/OM * MA/AB =1
2/1 * CO/OM * 2/5 =1
4/5 * CO/OM =1
CO/OM = 5/4 = 1,25
Ответ: 1,25

7.

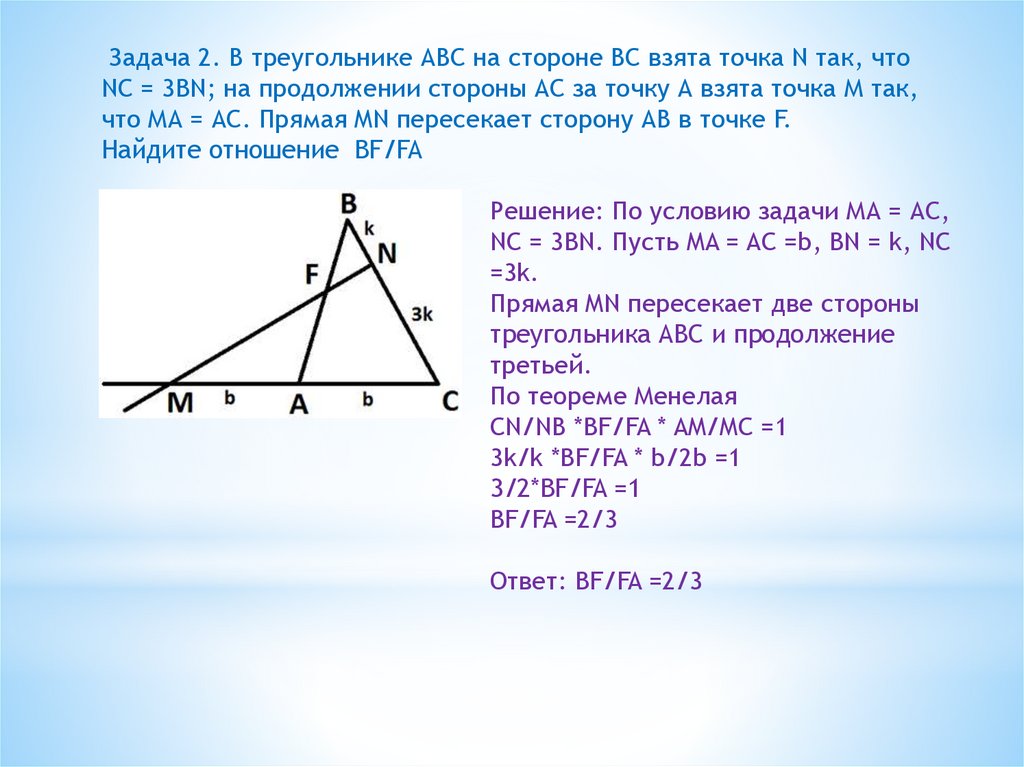
Задача 2. В треугольнике АВС на стороне ВС взята точка N так, что
NC = 3BN; на продолжении стороны АС за точку А взята точка М так,
что МА = АС. Прямая MN пересекает сторону АВ в точке F.
Найдите отношение BF/FA
Решение: По условию задачи МА = АС,
NC = 3BN. Пусть MA = AC =b, BN = k, NC
=3k.
Прямая MN пересекает две стороны
треугольника АВС и продолжение
третьей.
По теореме Менелая
СN/NВ *BF/FA * AM/MC =1
3k/k *BF/FA * b/2b =1
3/2*BF/FA =1
BF/FA =2/3
Ответ: BF/FA =2/3

8.

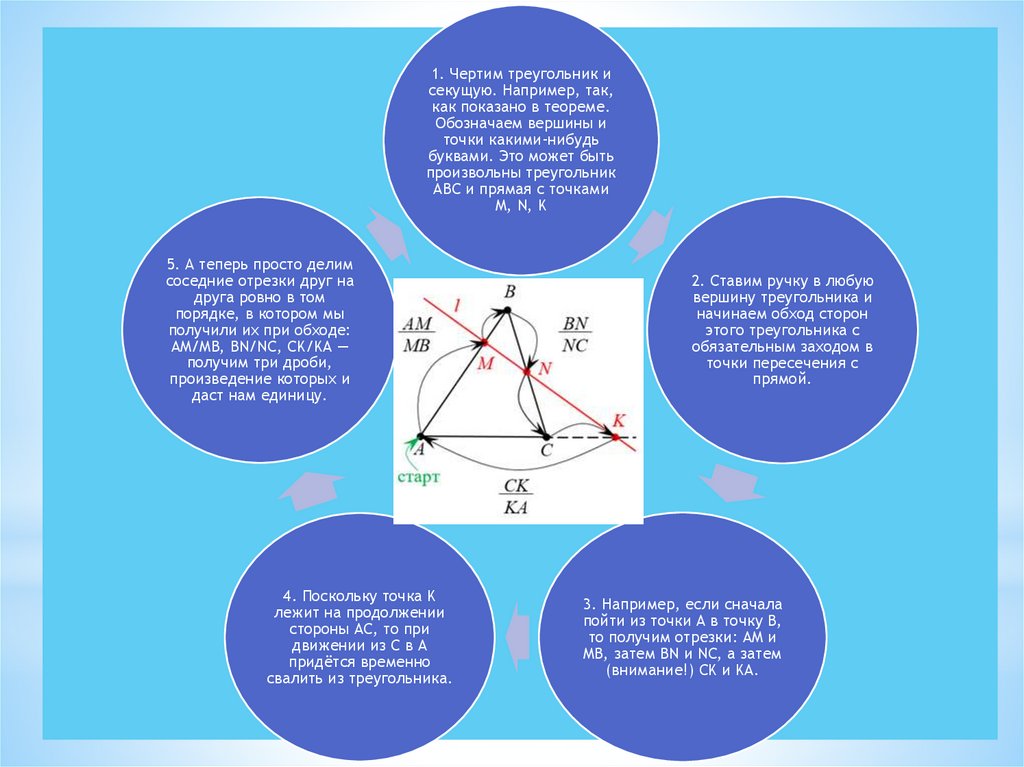
1. Чертим треугольник и
секущую. Например, так,
как показано в теореме.
Обозначаем вершины и
точки какими-нибудь
буквами. Это может быть
произвольны треугольник
ABC и прямая с точками
M, N, K
5. А теперь просто делим
соседние отрезки друг на
друга ровно в том
порядке, в котором мы
получили их при обходе:
AM/MB, BN/NC, CK/KA —
получим три дроби,
произведение которых и
даст нам единицу.
4. Поскольку точка K
лежит на продолжении
стороны AC, то при
движении из C в A
придётся временно
свалить из треугольника.
2. Ставим ручку в любую
вершину треугольника и
начинаем обход сторон
этого треугольника с
обязательным заходом в
точки пересечения с
прямой.
3. Например, если сначала
пойти из точки A в точку B,
то получим отрезки: AM и
MB, затем BN и NC, а затем
(внимание!) CK и KA.

9.

И сразу
пара
замечаний.
1. Что будет,
если прямая l
пройдёт через
вершину
треугольника?
2. Что будет,
если выбрать
другую вершину
для старта или
пойти в другую
сторону?
Ответ: ничего.
Теорема
Менелая в
этом случае не
работает.
Ответ: будет то
же самое.
Просто
изменится
последователь
ность дробей.

10.

*
* Научно-популярный физико-математический
журнал КВАНТ №3, 1990 г.
* https://ege-ok.ru И.В. Фельдман, репетитор
по математике
* https://www.berdov.com Павел Бердов,
репетитор по математике