Применение теоремы менелая к решению планиметрических и стереометрических задач

1.

ПРИМЕНЕНИЕ
ТЕОРЕМЫ МЕНЕЛАЯ К
РЕШЕНИЮ
ПЛАНИМЕТРИЧЕСКИХ И
СТЕРЕОМЕТРИЧЕСКИХ
ЗАДАЧ
Проектная работа
ученицы 10 "A" класса
Лицея для одарённых детей
ГБОУ “ДАТ “Солнечный город”
Боттаевой Элины
Руководитель: Чепрасова Елена Петровна
Нальчик, 2024

2.

АКТУАЛЬНОСТЬ ТЕМЫ: Школьникам
часто предлагают задачи, в которых необходимо найти
отношение сторон или площадей треугольников. И при решении задач такого
типа теорема Менелая будет очень функциональна. Поэтому полезно
ознакомиться с данной теоремой и провести небольшое исследование. В
дальнейшем полученные знания пригодятся при решении заданий ЕГЭ.
ПРЕДМЕТ ИССЛЕДОВАНИЯ: многообразие планиметрических и
стереометрических задач, для решения которых применима теорема
Менелая.
ГИПОТЕЗА: решение задач с помощью теоремы
Менелая более рационально, чем их решение другими способами.
ЦЕЛЬ ИССЛЕДОВАНИЯ: заключается в расширении знаний
о разнообразии задач, которые можно решить, применяя теорему Менелая,
и более подробном изучении способов использования теоремы.

3.

ЗАДАЧИ ПРОЕКТА:
01
Изучить
03
Сравнить
теорему Менелая
Решения задач с
помощью теоремы и
обычным способом
02
Рассмотреть
04
Сделать
Применение теоремы при
решении планиметрических
и стереометрических задач
Заключение о пользе данной
теоремы и её применении в
решении задач

4.

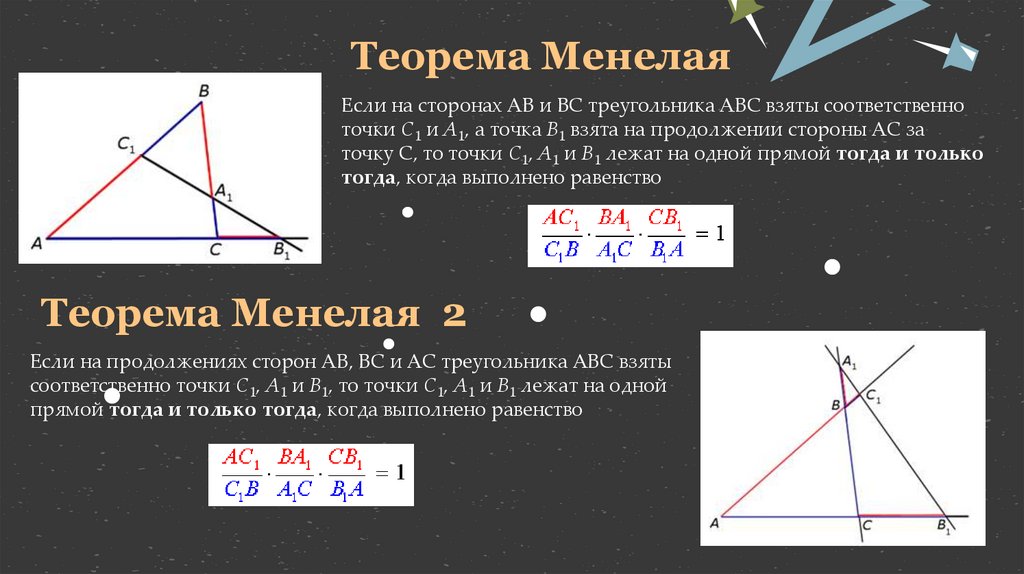
Теорема Менелая
Если на сторонах AB и BC треугольника ABC взяты соответственно
точки C1 и A1, а точка B1 взята на продолжении стороны AC за
точку C, то точки C1, A1 и B1 лежат на одной прямой тогда и только
тогда, когда выполнено равенство
Теорема Менелая 2
Если на продолжениях сторон AB, BC и AC треугольника ABC взяты
соответственно точки C1, A1 и B1, то точки C1, A1 и B1 лежат на одной
прямой тогда и только тогда, когда выполнено равенство

5.

ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
Докажем, что если точки
равенство
C1, A1 и B1 лежат на одной прямой, то выполнено
Для этого проведём через точку C прямую, параллельную прямой AB, и обозначим
буквой D её точку пересечения с прямой C1B1
Поскольку треугольник AC1B1 подобен треугольнику
CDB1, то выполнено равенство
Поскольку треугольник C1BA1 подобен треугольнику
DCA1, то выполнено равенство
Перемножив равенства, получим

6.

ПЛАНИМЕТРИЧЕСКИЕ
ЗАДАЧИ
Попробуем применить теорему
Менелая для решения
планиметрических задач,
которые встречались среди заданий
EГЭ прошлых
лет и в пособиях для
подготовки к экзамену этого года.

7.

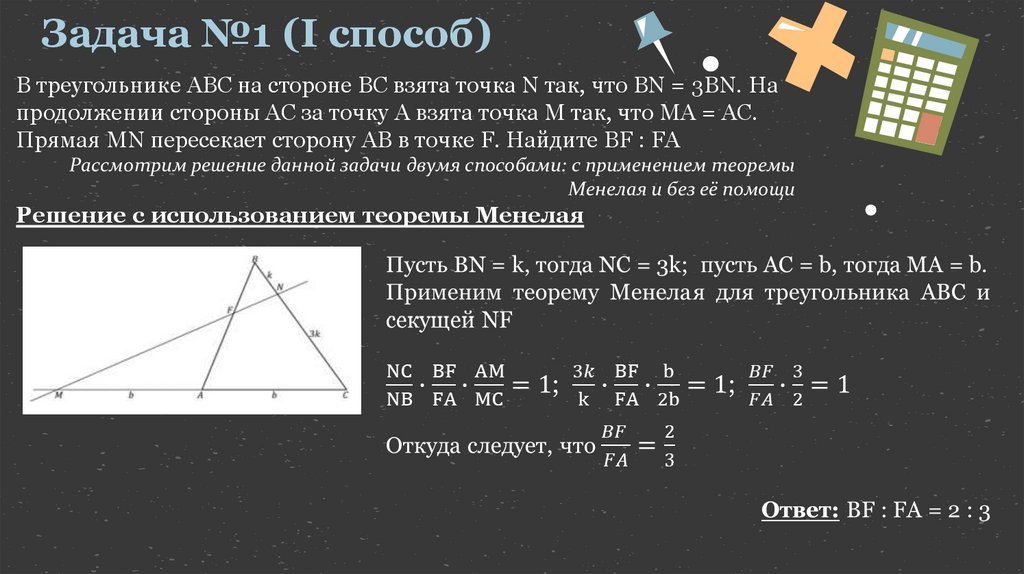
Задача №1 (I способ)
В треугольнике ABC на стороне BC взята точка N так, что BN = 3BN. На
продолжении стороны AC за точку A взята точка M так, что MA = AC.
Прямая MN пересекает сторону AB в точке F. Найдите BF : FA
Рассмотрим решение данной задачи двумя способами: с применением теоремы
Менелая и без её помощи
Решение c использованием теоремы Менелая

8.

Задача №1 (II способ)
Решение без использования теоремы Менелая
Сделаем дополнительное построение: проведём отрезок AK ∥ BC. Пусть
BN = k, тогда NC = 3k;
пусть AC = b, тогда MA = b.
Рассмотрим треугольники MKA и MNC. ∠AMK = ∠CMN – общий угол для
∆MKA и ∆MNC; ∠MKA = ∠MNC как соответственные углы, образованные
при пересечении параллельных прямых AK и BC (AK ∥ BC по
дополнительному построению) и секущей MN, K ∈ MN. Следовательно, ∆ MKA ~ ∆MNC по двум углам.

9.

Задача №2

10.

СТЕРЕОМЕТРИЧЕСКИЕ
ЗАДАЧИ
Рассмотрим применение теоремы
Менелая для упрощения
вычислений при решении
стереометрических задач

11.

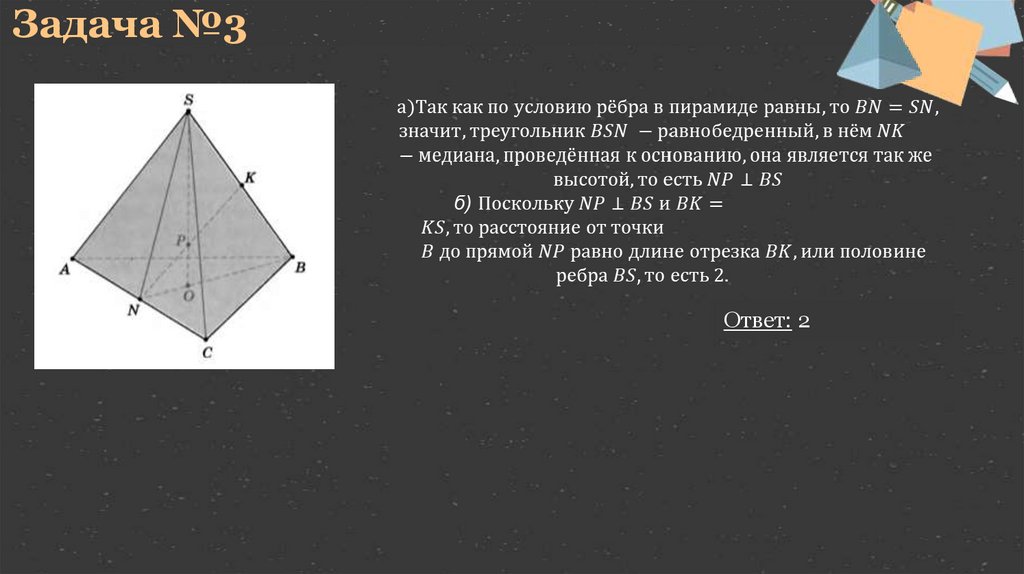
Задача №3
Ответ: 2

12.

Заключение
В процессе исследования я научилась решать
планиметрические и стереометрические задачи с
использованием теоремы Менелая. Выяснила какие случаи
решения возможны. Поняла, каким образом стоит применять
данную теорему в разных случаях. Благодаря данному проекту
я смогла систематизировать уже имеющиеся представления по
данной теме, пополнить «багаж» знаний задачами, которые мы
не изучали на уроках геометрии. Знания, полученные мной в
процессе подготовки данного проекта, помогут в будущем при
решение олимпиадных задач, задач ЕГЭ.
СПАСИБО
ЗА
ВНИМАНИЕ!