Теорема Эйлера. Опорные знания

1. Лекция №2 Теорема Эйлера

2. Опорные знания

Замечательные точки в треугольнике
Центр описанной около треугольника окружности
лежит на пересечении
серединных перпендикуляров к сторонам
треугольника.
Центр вписанной в треугольник окружности лежит
на пересечении
биссектрис треугольника.
Точка пересечения высот – ортоцентр. Соединяя
основания высот получим ортотреугольник.
Точка пересечения медиан – центроид. Соединяя
середины сторон треугольника получим серединный
треугольник.

3. Исследовательская работа, выдвижение гипотезы

1. Начертите произвольный треугольник АВС.
2. Постройте в нем ортоцентр.
3. Постройте центроид.
4. Постройте центр описанной окружности.
5. Посмотрите на расположение трех построенных
точек.
6. Выдвиньте гипотезу об их расположении.
7. Что можно предположительно сказать о
расстоянии между этими точками?
8. Уточните гипотезу.

4. Эвристическая беседа

Сначала рассмотрим отношение длин отрезков.
Какой математический метод, как правило, используется при
обосновании отношений отрезков? В каких теоремах идет речь об
отношении отрезков?
Метод подобия. В теоремах о признаках подобия треугольников.
О пересечении медиан. О средней линии. О биссектрисе угла
треугольника.
Есть ли кажущиеся подобными треугольники, в которых
сходственными сторонами были бы отрезки HG и GO? Если
доказать подобие треугольников, то эти стороны будут
пропорциональны.
Как доказать подобие треугольников? Надо воспользоваться
одним из признаков. Выясним, какие соответствующие элементы
двух треугольников можем найти. Будем отсеивать ненужные
варианты.

5. Подзадача

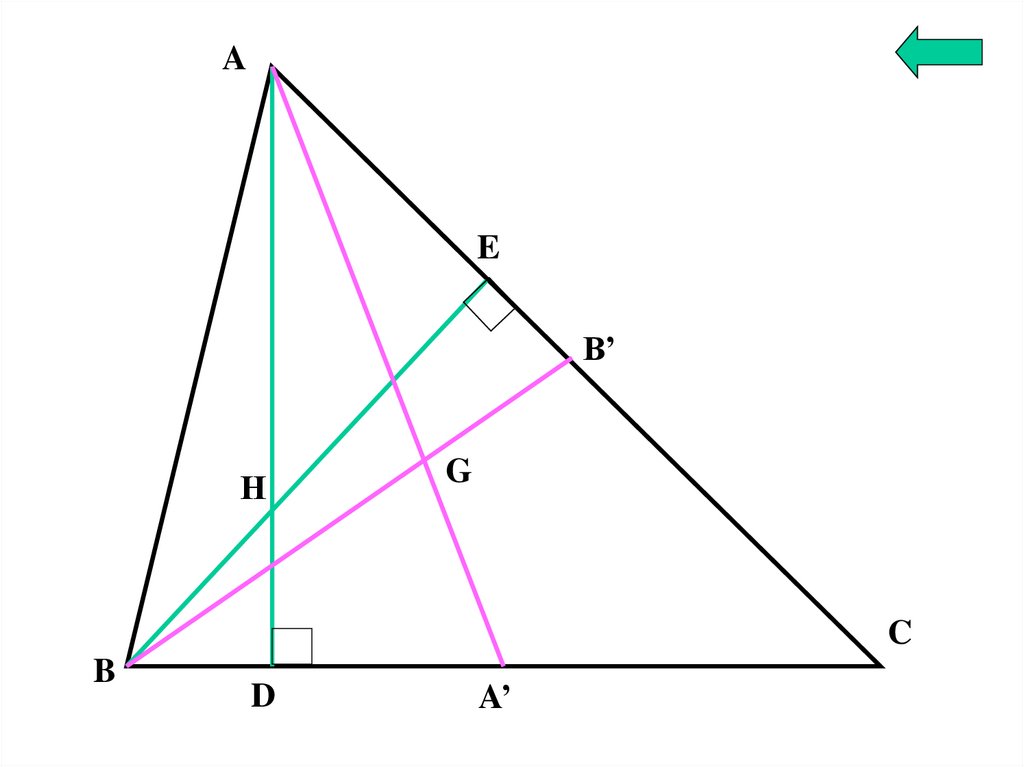
Постройте серединный треугольник.
Как он соотносится с исходным треугольником?
Каков коэффициент подобия?
В треугольнике АВС AD –
высота.
В треугольнике А’В’С’ A’D’ – высота.
Соответствующие отрезки в подобных
треугольниках пропорциональны.
Значит высоты исходного и серединного
треугольников относятся как 2:1, как и их части АН
и А’О.

6. План

1. Установить подобие треугольников AHG и
A’OG, воспользовавшись свойством медиан,
подобием исходного и серединного
треугольника, равенством накрест лежащих
углов.
2. Из подобия сделать вывод о
пропорциональности HG и GO.
3. Доказать, что три точки лежат на одной
прямой, или иначе…
отрезки, принадлежащие сторонам угла,
составляют развернутый угол.

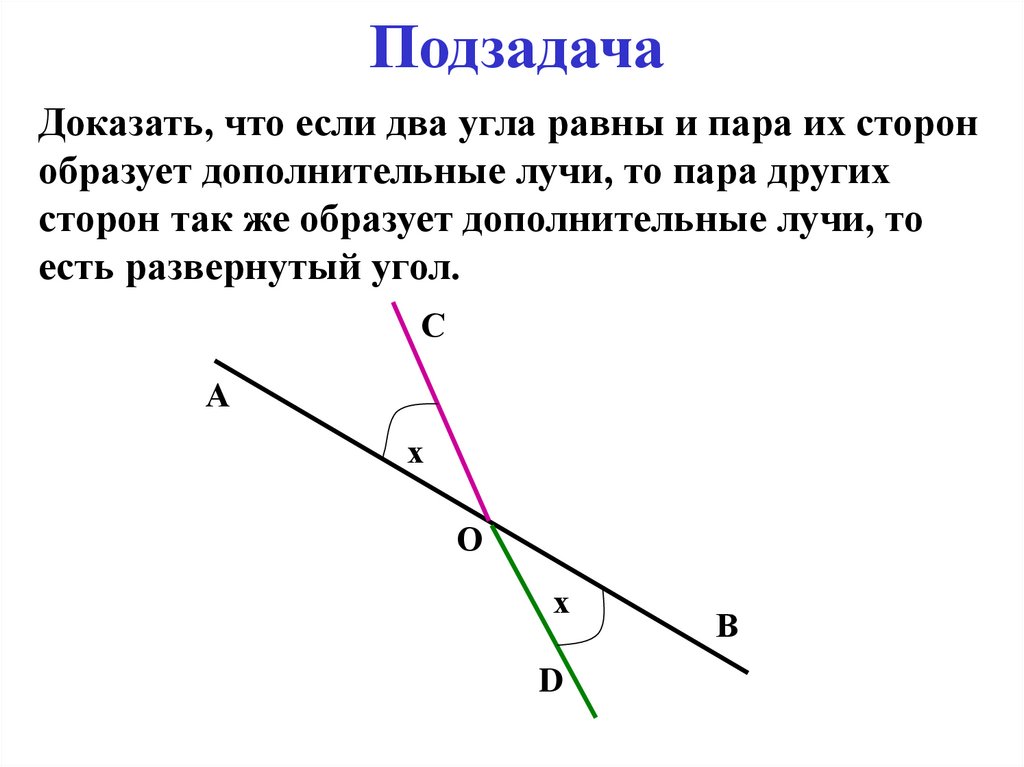
7. Подзадача

Доказать, что если два угла равны и пара их сторон
образует дополнительные лучи, то пара других
сторон так же образует дополнительные лучи, то
есть развернутый угол.
С
А
х
О
х
D
В

8. Доказательство:

1. AD BC, A’O BC, то AD||A’O - как два перпендикуляра к
одной прямой.
2. HAG= GA’O – как накрест лежащие углы при AD||A’O
и секущей AA’.
3. AG:GA’=2:1 – по теореме о пересечении медиан
треугольника.
4. АВС A’B’C’ по третьему признаку подобия, стороны
ABC пропорциональны средним линиям. k=2. Тогда
пропорциональны высоты и их соответствующие части:
AH:A’О=2:1.
5. AHG GOA’ (по первому признаку подобия), k=2, тогда
HG:GO=2:1.
6. HGA= OGA’ (из подобия), A,G,A’ – лежат на одной
прямой, то H,G,O – лежат на одной прямой (см.
подзадачу).

9. Теорема Чевы

Опорные знания
Отрезок, соединяющий вершину
треугольника с некоторой точкой на
противоположной стороне, называется
ЧЕВИАНОЙ.
Прямые конкурентны, если все они проходят
через одну точку.
Площади треугольников с равными высотами
пропорциональны
основаниям треугольников.

10. Свойство пропорции

a c a c
b d b d

11. Формулировка

Если три чевианы AX, BY, CZ
треугольника АВС конкурентны, то
|BX|:|XC| * |CY|:|YA| * |AZ|:|ZB|=1
A
Z
Y
P
C
B
X

12. Поиск решения

1. Соотнесем аналитическую запись и чертеж.
2. В состав каких фигур входят отрезки,
составляющие отношения? Например, ВХ и ХС?
3. Чем являются эти отрезки в треугольниках?
4. В чем особенность этих пар треугольников?
5. С отношением каких величин связано
отношение оснований треугольников с равными
высотами?
6. Выразим отношения через площади
треугольников сначала с вершиной А, затем Р.

13. Доказательство

BX S ABX S PBX S ABX S PBX S ABP
1.
XC S AXC S PXC
S AXC S PXC S APC
SCPY
S BYC SCPY
S BPC
CY S BYC
2.
YA S ABY S PAY S ABY S PAY S ABP
AZ S APC
3.
ZB S BPC
4. Перемножим выражение отношений отрезков
через площади треугольников.

14.

A
C
B

15.

A
E
Н
C
B
D

16.

A
E
B’
Н
G
C
B
D
A’

17.

A
E
B’
Н
O
G
C
B
D
A’

18.

A
E
B’
Н
O
G
C
B
D
A’

19. Гипотеза 1

Ортоцентр, центроид и центр
описанной окружности
произвольного треугольника лежат
на одной прямой.

20.

A
E
B’
Н
O
G
C
B
D
A’

21. Гипотеза 2

Ортоцентр, центроид и центр
описанной окружности
произвольного треугольника лежат
на одной прямой.
Центроид делит расстояние от
ортоцентра до центра описанной
окружности в отношении 2:1.

22.

A
E
B’
Н
O
G
C
B
D
A’

23.

A
E
D’
Н
B’
O
G
C
B
D
A’