Похожие презентации:
Решение систем линейных уравнений
1. Решение систем линейных уравнений
2. Графический способ решения систем линейных уравнений
3. Дана система линейных уравнений
x y 1,2 x y 4.
Рассмотрим каждое
уравнение в
отдельности.
Геометрической
иллюстрацией уравнения с
двумя неизвестными служит
его график на координатной
плоскости.
4. Дана система линейных уравнений
первоеx y 1, Рассмотрим
уравнение
2 x y 4. x y 1
Выразим из этого
уравнения y через x .
y x 1
5.
Данное уравнение можно рассматриватькак формулу, задающую линейную
функцию.
y x 1
Поэтому графиком данного уравнения
является прямая.
Для построения графика найдем две точки.
1)
x 0, y 1;
2)
x 2, y 3.
6. Построим график
y x 17. Вернемся к системе линейных уравнений
второеx y 1, Рассмотрим
уравнение
2 x y 4. 2 x y 4
Выразим из этого
уравнения y через x .
y 2 x 4
8.
Данное уравнение также как и первоеможно рассматривать как формулу,
задающую линейную функцию.
y 2 x 4
Поэтому графиком данного уравнения
является прямая.
Для построения графика найдем две точки.
1)
x 0, y 4;
2)
x 2, y 0.
9. Построим график второй функции
y x 1y 2 x 4
10. Найдем координаты точки пересечения прямых
y x 1y x 1
A(1; 2)
y 2 x 4
Ответ:
(1; 2)
11. Для графического решения системы нужно:
1. Построить графики каждого изуравнений системы.
2. Найти координаты точки пересечения
построенных прямых (если они
пересекаются)
На плоскости возможны три случая
взаимного расположения двух прямых
― графиков уравнений системы
12. Три случая взаимного расположения двух прямых
1. Прямые пересекаются.То есть имеют одну общую точку.
Тогда система
уравнений имеет
единственное
решение.
Например, как в
рассмотренной системе
y x 1
y 2 x 4
13. Три случая взаимного расположения двух прямых
2. Прямые параллельны.То есть не имеют общих точек.
Тогда система
уравнений
решений не имеет.
Например:
y x 1
y x 2
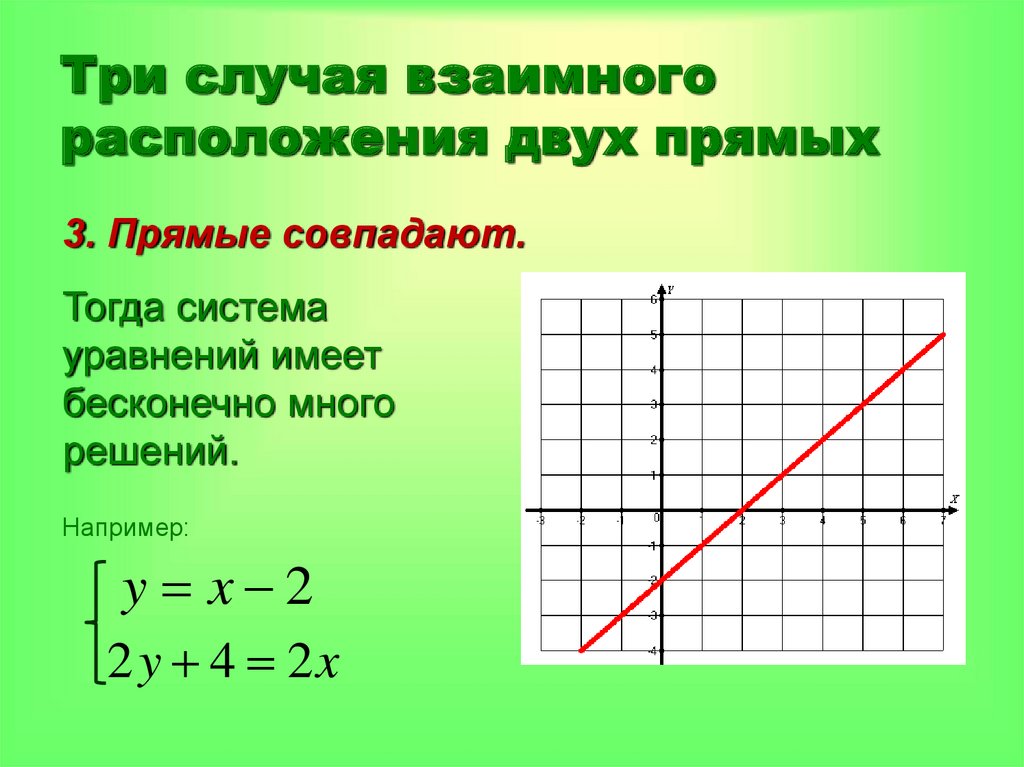
14. Три случая взаимного расположения двух прямых
3. Прямые совпадают.Тогда система
уравнений имеет
бесконечно много
решений.
Например:
y x 2
2 y 4 2x
15.
Материал дляповторения :
Красный учебник;
стр. 74 – 79, § 13
15
16. Способ подстановки при решении систем линейных уравнений
17. Способ подстановки
Этот способ удобен тогда, когда хотя бы одиниз коэффициентов при x или y равен 1 или -1.
Дана система уравнений Рассмотрим каждое
2 x y 4,
3x 4 y 27.
(1)
(2)
1) Выразим одно из
неизвестных через другое
неизвестное из любого
уравнения.
уравнение в
отдельности.
2 x y 4,
y 4 2 x
y 4 2x
(1)
18.
Способ подстановкиВернемся в систему:
2) Полученное для
y выражение
подставим вместо
данной
неизвестной во
второе уравнение.
y 2 x 4,
3x 4 y 27.
y 2 x 4,
3x 4(2 x 4) 27.
(1)
(2)
(1)
(2)
Получилось уравнение с одной
неизвестной
19.
Способ подстановки3) Выходим из системы
и решаем уравнение с
одной неизвестной:
3 x 4(2 x 4) 27,
3 x 8 x 16 27,
11x 16 27,
11x 27 16,
11x 11,
x 1.
Возвращаемся в
систему:.
y 2 x 4, (1)
x 1. ( 2)
20.
Способ подстановкиВозвращаемся в
систему:
y 2 x 4, (1)
x 1. ( 2)
4) Подставим найденное значение x в первое
уравнение и найдем вторую неизвестную
y 2 1 4, (1)
x 1. (2)
Запишем ответ.
y 6, (1)
x 1 . ( 2)
Ответ:
(1; 6)
21.
Материал дляповторения :
Красный учебник;
стр. 80 – 83, § 14
21
22. Способ сложения при решении систем линейных уравнений
Этот способ используюттогда, когда нет
коэффициентов при x или y
равных 1 или -1.
23. Способ сложения
Задача 1. Решить систему уравнений7 x 2 y 27, (1)
5 x 2 y 33. (2)
В тех случаях, когда в обоих линейных
уравнениях системы при каком-либо из
неизвестных коэффициентами являются
противоположные или одинаковые числа,
удобно применять способ алгебраического
сложения уравнений.
24. Способ сложения
Задача 1. Решить систему уравнений7 x 2 y 27, (1)
5 x 2 y 33. (2)
Предположим, что числа x
и y ─ решения системы,
при которых оба равенства
системы равны.
7 x 2 y 27,
+
5 x 2 y 33.
Сложим эти равенства.
В результате получим
тоже верное равенство,
(7х – 2у) + (5х + 2у) = 27 + 33
так как к равному
12 x 60
прибавляли равное.
x 5
25. Способ сложения
Задача 1. Решить систему уравненийВернемся в систему, записав
одно из исходных уравнений и
полученное значение x.
7 x 2 y 27, (1)
5 x 2 y 33. (2)
x 5, (1)
5 x 2 y 33. (2)
5 5 2 y 33,
2 y 33 25,
2 y 8; y 4.
Подставим найденное значение
x во второе уравнение, найдем
вторую неизвестную.
Тогда пара чисел (5; 4) и будет
решением системы.
Ответ: (5; 4)
26. Способ сложения
Задача 2. Решить систему уравнений1) Выберем неизвестную
(1) (например x),
2 x 5 y 1,
3 x 4 y 5. ( 2)
уравняем коэффициенты
при х умножением на
соответствующие числа.
2 x 5 y 1, 3
2
3
x
4
y
5
6 x 15 y 3,
6 x 8 y 10.
27. Способ сложения
Задача 2. Решить систему уравнений(1)
2 x 5 y 1,
3 x 4 y 5. ( 2)
2) Вычтем одно
уравнение из другого.
6 x 15 y 3,
─
6 x 8 y 10.
(6х + 15у) – (6х + 8у) = - 3 – (- 10)
6х + 15у – 6х – 8у = - 3 +10
7 y 7, y 1
3) Решим полученное
уравнение с одним
неизвестным
4) Вернемся в систему,
записав одно из исходных
уравнений и полученное
значение y
2 x 5 y 1, (1)
y 1. ( 2)
28. Способ сложения
4) Вернемся в систему,записав одно из исходных
уравнений и полученное
значение y
2 x 5 y 1, (1)
y 1. ( 2)
5) Подставим найденное
2 x 5 1 1,
значение y в первое
2 x 6,
x 3.
уравнение, найдем
вторую неизвестную.
Тогда пара чисел (-3; 1) и будет решением системы.
Ответ: ( - 3; 1)
29.
Материал дляповторения :
Красный учебник;
стр. 83 – 86, § 15
29




























 Математика
Математика