Задачи на построение сечений куба

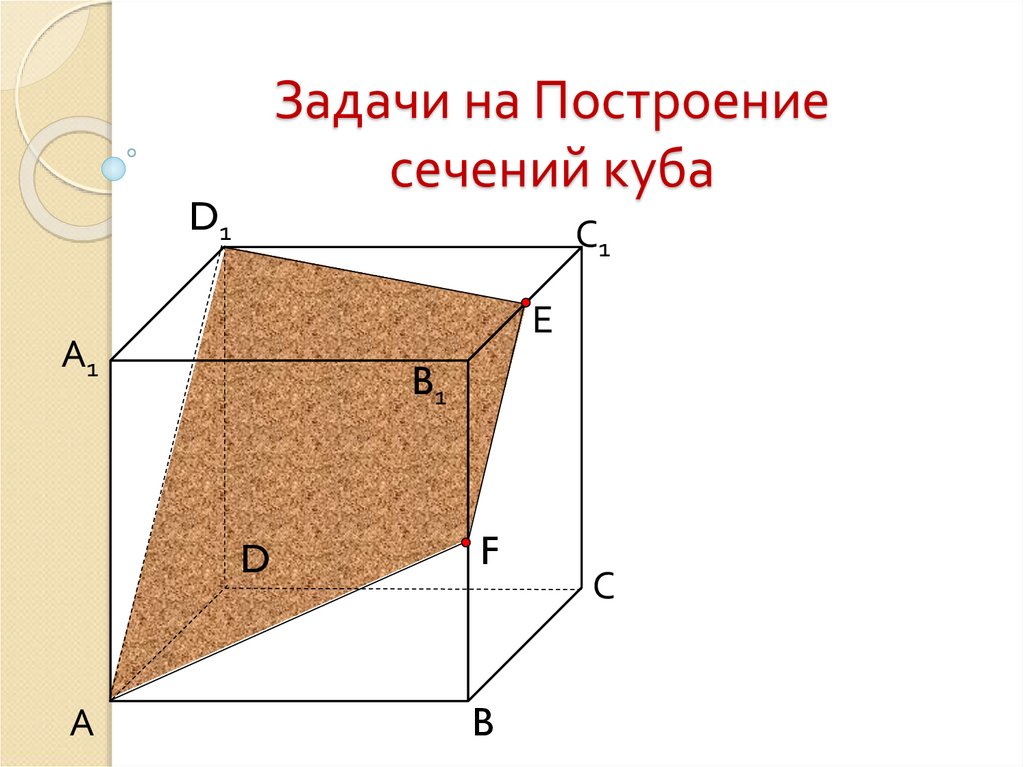
1. Задачи на Построение сечений куба

D1
С1
Е
А1
B1
D
А
F
B
С

2. Проверочная работа.

1 вариант
2 вариант
1. тетраэдр
1. параллелепипед
2. Свойства параллелепипеда

3. Секущей плоскостью куба называется любая плоскость, по обе стороны от которой имеются точки данного куба.

Секущая плоскость пересекает грани куба по
отрезкам.
Многоугольник, сторонами которого являются
данные отрезки, называется сечением куба.
Сечениями куба могут быть треугольники,
четырёхугольники, пятиугольники и
шестиугольники.
При построении сечений следует учитывать тот
факт, что если секущая плоскость пересекает две
противоположные грани по каким-то отрезкам, то
эти отрезки параллельны. (Объясните почему).

4.

B1
C1
D1
A1
M
K
ВАЖНО!
B
С
D
ЕслиAсекущая плоскость пересекает
противоположные грани, то она
K DCC1
пересекает их по параллельным
M BCC1
отрезкам.

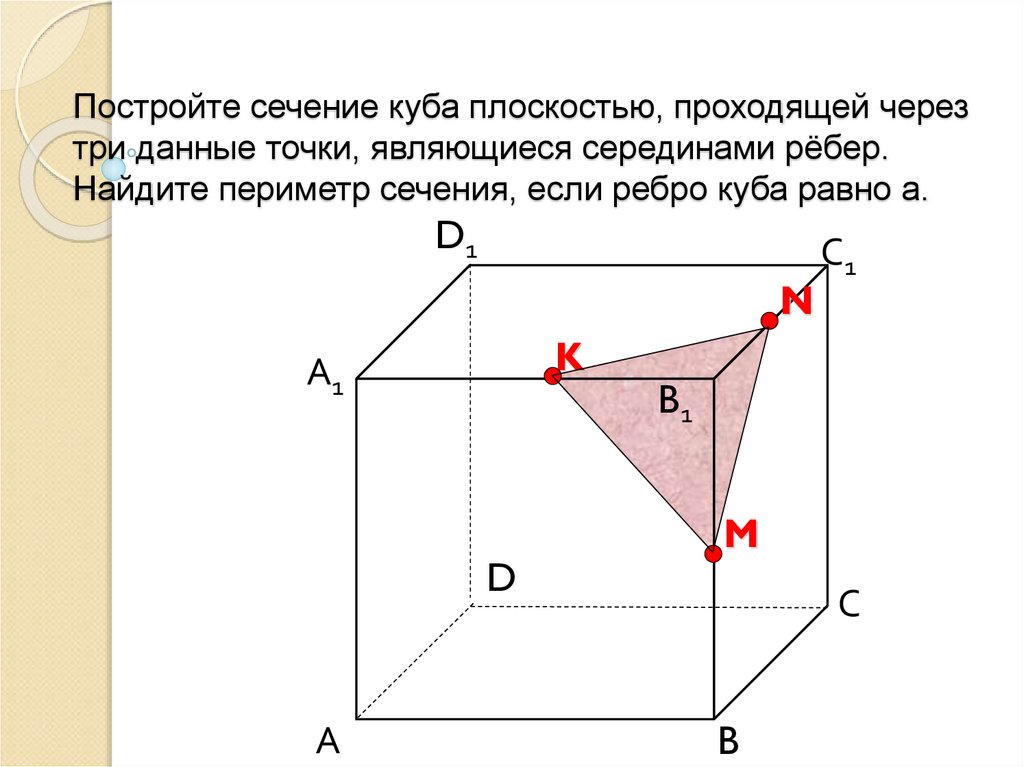
5. Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами рёбер. Найдите периметр сечения,

если ребро куба равно а.
D1
N
K
А1
D
А
С1
B1
M
С
B

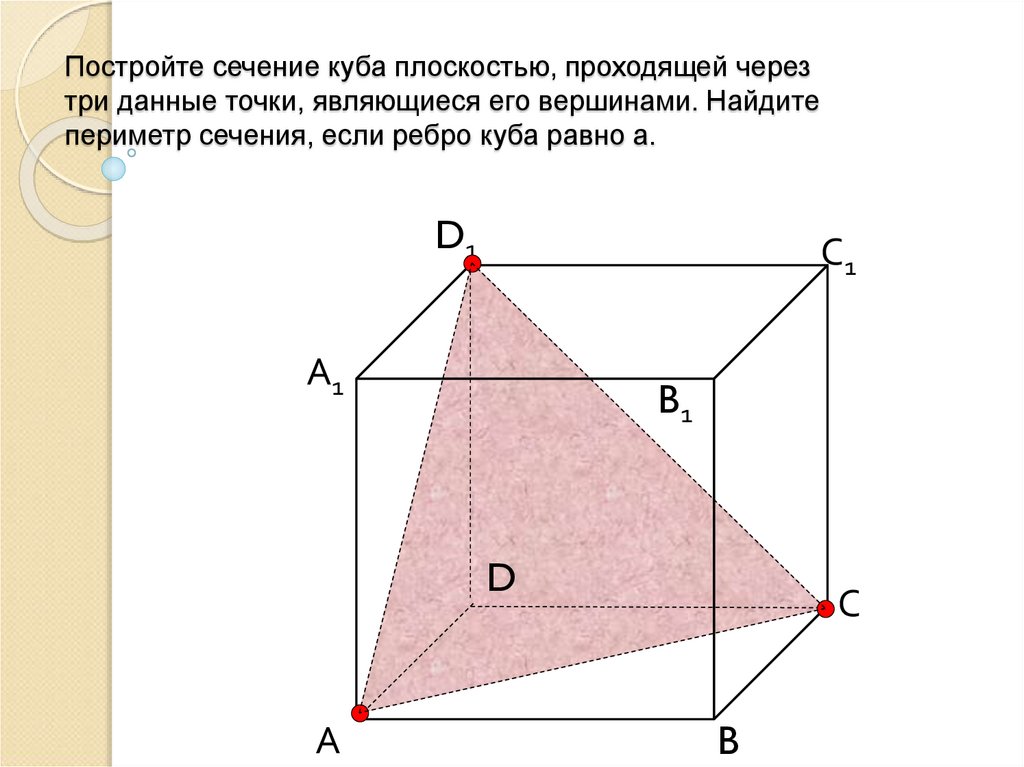
6. Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся его вершинами. Найдите периметр сечения, если

ребро куба равно а.
D1
С1
А1
B1
D
А
С
B

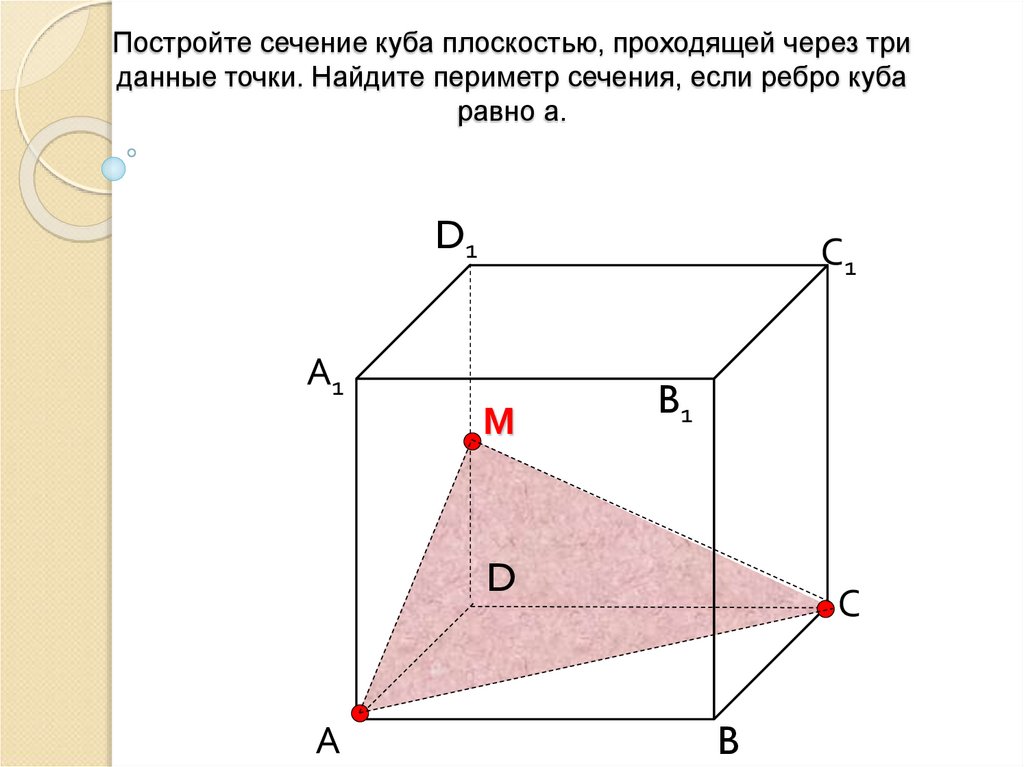
7. Постройте сечение куба плоскостью, проходящей через три данные точки. Найдите периметр сечения, если ребро куба равно а.

D1
С1
А1
М
B1
D
А
С
B

8. Постройте сечение куба плоскостью, проходящей через три данные точки. Найдите периметр сечения, если ребро куба равно а.

D1
С1
А1
B1
N
D
А
С
B

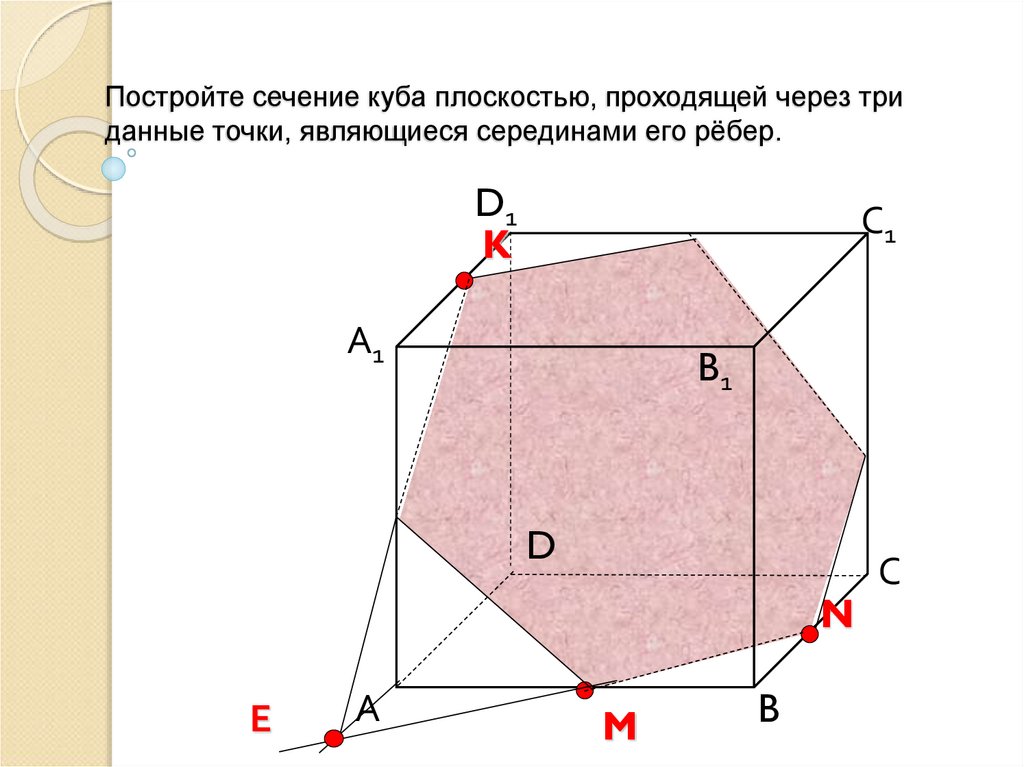
9. Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами его рёбер.

С1
D1
B1
А1
K
D
С
N
Е
А
M
B

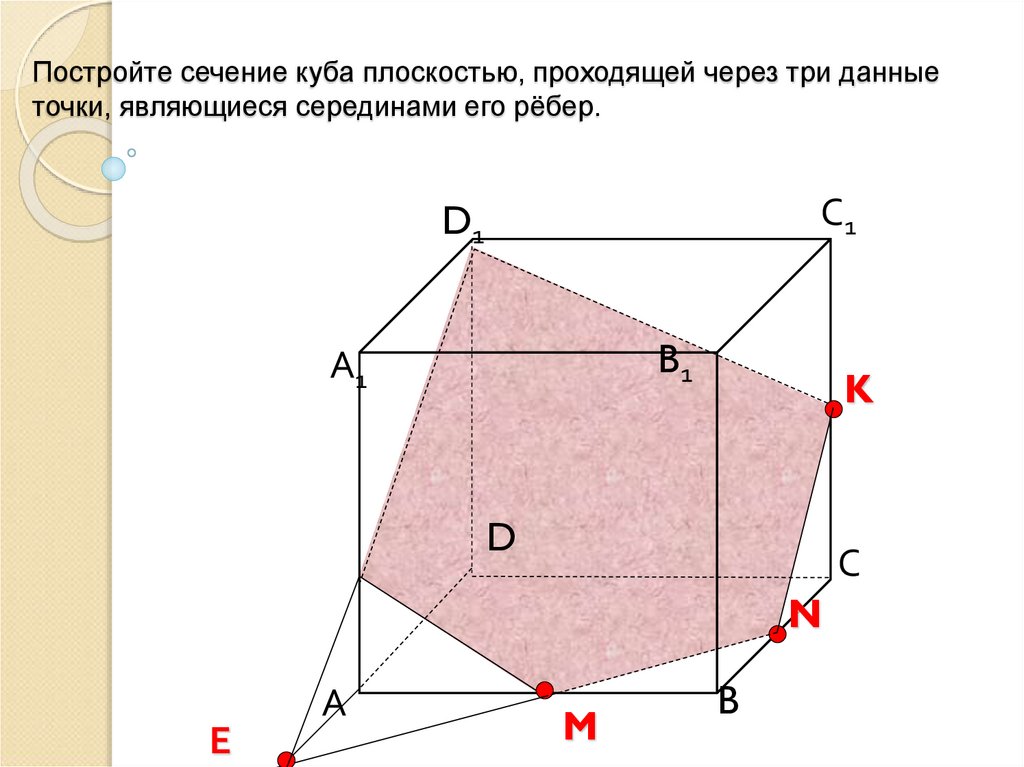
10. Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами его рёбер.

D1
K
С1
А1
B1
D
N
Е
А
M
B
С

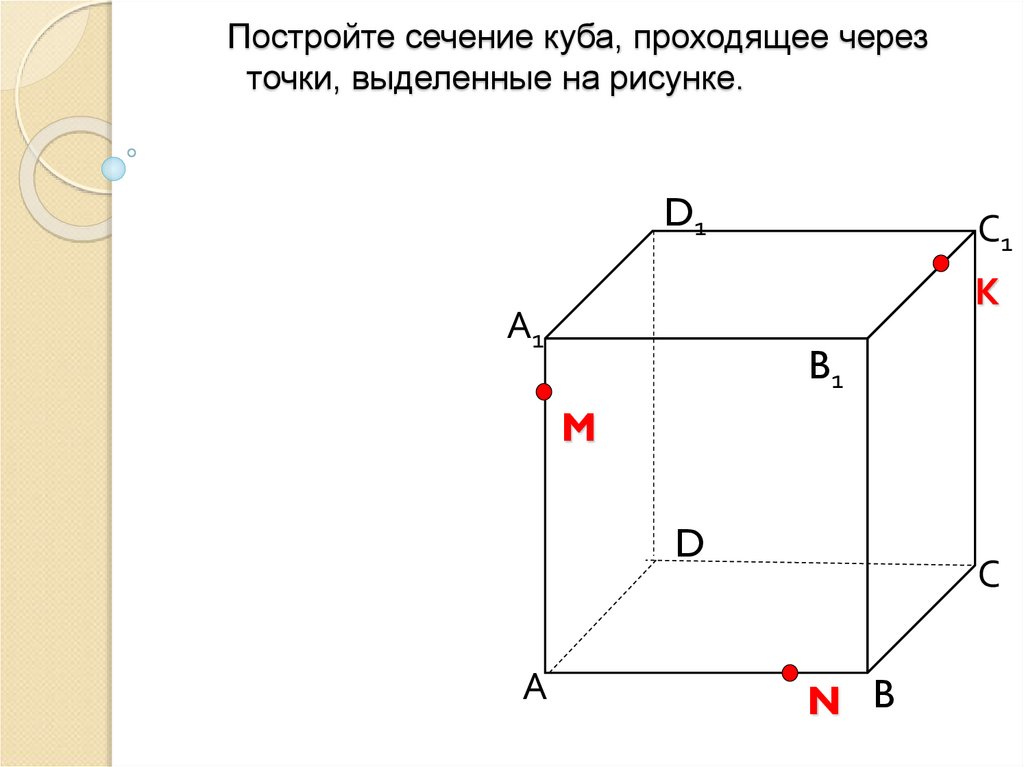
11. Постройте сечение куба, проходящее через точки, выделенные на рисунке.

D1
С1
К
А1
B1
M
D
А
С
N B