Похожие презентации:
Определенный интеграл. Формула Ньютона-Лейбница
1. Определенный интеграл. Формула Ньютона-Лейбница
2.
Определение криволинейной трапецииY
Криволинейная
трапеция
f(x)
a
b
X
Пусть в декартовой системе координат дана фигура, ограниченная :
1) Осью х
2) Прямой х = а
3) Прямой х = b
4) Графиком непрерывной и неотрицательной на отрезке [a; b] функции y = f(x)
3.
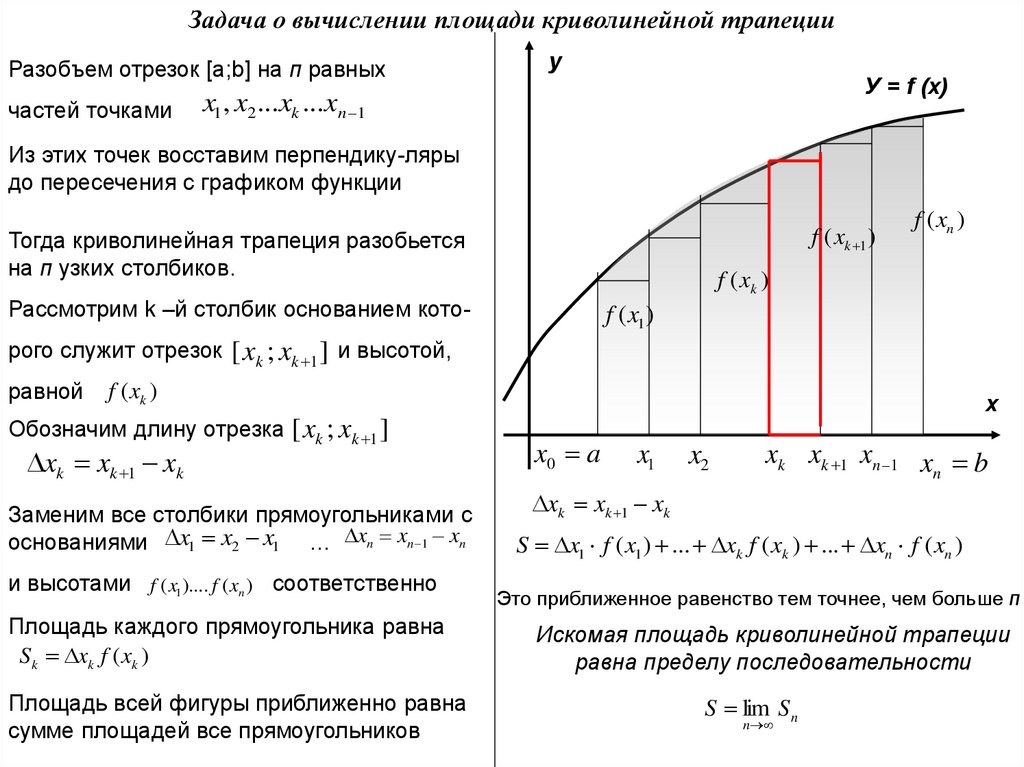
Задача о вычислении площади криволинейной трапецииРазобъем отрезок [a;b] на п равных
частей точками
у
У = f (x)
x1 , x2 ...xk ...x n 1
Из этих точек восставим перпендику-ляры
до пересечения с графиком функции
Тогда криволинейная трапеция разобьется
на п узких столбиков.
f ( xk 1 )
f ( xk )
Рассмотрим k –й столбик основанием кото-
рого служит отрезок
равной
f ( xn )
f ( x1 )
[ xk ; xk 1 ] и высотой,
f ( xk )
Обозначим длину отрезка [ xk ; xk 1 ]
xk xk 1 xk
Заменим все столбики прямоугольниками с
основаниями x1 x2 x1 … xn xn 1 xn
и высотами f ( x1 ).... f ( xn ) соответственно
Площадь каждого прямоугольника равна
Sk xk f ( xk )
Площадь всей фигуры приближенно равна
сумме площадей все прямоугольников
х
x0 a
x1
x2
xk xk 1 xn 1 x b
n
xk xk 1 xk
S x1 f ( x1 ) ... xk f ( xk ) ... xn f ( xn )
Это приближенное равенство тем точнее, чем больше п
Искомая площадь криволинейной трапеции
равна пределу последовательности
S lim S n
n
4.
Понятие определенного интегралаS lim S n
n
Этот предел называют определенным интегралом функции
y = f(x) по отрезку [a;b] и обозначают так:
b
lim Sn f ( x)dx
n
a
читают: интеграл от а до b эф от икс дэ икс
а – нижний предел
b – верхний предел
5.
Множество всех первообразных для функции y = f(x) на промежутке Хназывают неопределенным интегралом и обозначают
f ( x)dx F ( x) C
lim S n называют определенным интегралом от y = f(x) по отрезку [a;b]
n
и обозначают :
b
lim Sn f ( x)dx
n
a
6.
ТЕОРЕМА. Если функция y = f(x) непрерывна на отрезке [a;b]. тосправедлива формула
b
f ( x)dx F (b) F (a)
a
Формула
Ньютона - Лейбница
где F(x) – первообразная для функции y = f(x)
На практике вместо записи
F (b) F (a)
используют
F ( x) ba
эту запись называют двойной подстановкой
7.
Формула Ньютона - Лейбницаb
f ( x)dx F ( x) ba
a
Вычислить определенный интеграл, значит:
1) найти первообразную подынтегральной функции y = f(x);
2) выполнить двойную подстановку
8.
Пример 1. Вычислить определенный интеграл1
2 x 1
e
dx
0
F ( x) ba F (b) F (a)
Решение:
1
e
0
1 2 x 1 1 1 2 1 1 2 0 1 1 3
dx e
e e
e e
0
2
2
2
2 x 1
f ( x)dx F ( x) C
9.
Пример 2. Вычислить определенный интеграл4x7 6x6 x4 1
dx
4
1
x
1
Решение:
1
1
4x7 6x6 x 4 1
4x7 6x6 x 4 1
3
2
4
dx
dx
4
x
6
x
1
x
dx
4
4
4
4
4
1
x
x
x
x
x
1
1
1
1
1
1
1
4
4
x
4 x 3 dx 6 x 2 dx dx x 4 dx
4
1
1
1
1
1 1 2 1 1
4
4
3
1
2
0 4 0 2 6
3
3
3
3
6
x
1
1
3
2
x
1
1
2
3
x
1
1
3
1 2
1 1
1
2
1 1 3
3
2
3 1 1
1
1








 Математика
Математика








