Похожие презентации:
Комбинаторика
1.
КомбинаторикаВиленкин Н.Я. Комбинаторика.
Виленкин Н.Я. Популярная комбинаторика.
Нефедов В.Н., Осипова В.А. Курс дискретной математики.
Липский В. Комбинаторика для программистов.
Андерсон Джеймс А. Дискретная математика и
комбинаторика.
1
2.
Задачи комбинаторики – пересчет и перечисление элементовв конечных множествах.
Задача пересчета – сколько элементов, принадлежащих
заданному конечному множеству, обладают заданным свойством.
Задача перечисления – выделение из конечного множества
всех элементов, удовлетворяющих заданному свойству.
2
3.
Если X n , то объект x может быть выбран из X n способами.Правило суммы. Если объект x может быть выбран m способами,
а объект y – другими n способами, то выбор «либо x , либо y » можно
сделать m n способами.
Правило произведения. Если объект x может быть выбран m
способами и после каждого из таких выборов объект y в свою очередь
может быть выбран n способами, то выбор упорядоченной пары x, y ,
можно сделать mn способами.
3
4.
Правило произведения. Если объект x может быть выбран nспособами и после каждого из таких выборов объект y в свою очередь
может быть выбран m способами, то выбор упорядоченной пары x, y
, можно сделать nm способами.
Пусть объект x выбирается из множества X a1 , a2 ,..., an .
Обозначим через X i – множество пар
x, y , в которых x ai .
Множества X i попарно не пересекаются и X i m i 1, n . Следовательно
n
i 1
n
n
i 1
i 1
X i X i m nm .
4
5.
Правило суммы. Если объект x может быть выбран m способами,а объект y – другими n способами, то выбор «либо x , либо y » можно
сделать m n способами.
Следствие. Пусть X 1 , X 2 , …, X k – попарно непересекающиеся
множества, тогда
k
i 1
k
Xi Xi .
i 1
Правило произведения. Если объект x может быть выбран m
способами и после каждого из таких выборов объект y в свою очередь
может быть выбран n способами, то выбор упорядоченной пары x, y ,
можно сделать mn способами.
Следствие. Если объект x1 может быть выбран n1 способами, после
чего объект x2 в свою очередь может быть выбран n2 способами и
i 2, m 1 , после выбора объектов x1 , x2 ,..., xi объект xi 1 может быть
выбран ni 1 способами, то выбор упорядоченной последовательности из
m объектов x1 , x2 ,..., xm можно сделать n1n2 ...nm способами.
5
6.
Формула включений и исключений.Пусть X i – конечные множества, i 1,2,..., n , n 2 . Тогда X 1
X2
...
Xn
X 1 X 2 ... X n X 1 X 2 X 1 X 3 ... X 1 X n ... X n 1 X n
n 1
X 1 X 2 X 3 X 1 X 2 X 4 ... X n 2 X n 1 X n ... 1 X 1 X 2 ...
Xn
.
Докажем методом математической индукции.
1. n 2 . Если X 1
X 2 , то X1
X 2 X1 X 2 . Если X 1
X 1 X 2 каждый элемент множества X 1
X1
X 2 , то в сумме
X 2 посчитан 2 раза, а значит,
X 2 X1 X 2 X1
X2 .
6
7.
Пусть формула справедлива для n множеств. ТогдаX1
X2
X1
...
X2
Xn
X n 1 X 1
X2
X n X n 1 X 1
...
X1 X 2 ... X n X1
X1
... 1
n 1
X n 1 X 1
X1 X 2 ... X n X1
X1
X2
X 3 X1
X2
X n 1
X 3 ... X1
X 3 X1
X2
X1
X2
...
X n 1
X2
X 2 X1
... 1 X1 X 2 ... X n
X n 1 X1 X n 1 X 2 X n 1 ... X n
Xn
X n ... X n 1
X 4 ... X n 2
X n 1
Xn
Xn
X n 1 ...
X 3 ... X1
X 4 ... X n 2
X2
X n 1
Xn
...
X 2 X1
X2
Xn
...
X n 1
Xn
X n 1
X n ... X n 1
Xn
Xn
n 1
X1
X2
... 1
1
n 2
n 1
X1
X n 1 X1
X
X3
X n 1
X n 1 ... X n 1
2
X3
...
X n 1 X 1
X2
...
Xn
X n 1
X3
...
Xn
X n 1
X n 1 X 1
X 2 ...
X n 1
X n 1
7
8.
ПримерВ НИИ работает несколько человек, причем все они знают
хотя бы по одному языку:
англ. – 6,
англ. и нем. – 4,
франц. – 7,
англ. и франц. – 2,
нем. – 6,
нем. и франц. – 3,
1) Сколько человек в НИИ?
все три языка – 1.
(6 + 7 + 6) – (4 + 2 + 3) + 1 = 11
2) Сколько человек знают только английский?
6 – (4 + 2) + 1 = 1
3) Сколько человек знают только французский? 7 – (2 + 3) + 1 = 3
8
9.
1. Из города A в город B ведут пять дорог, а из города B в город С – три. Сколькопутей, проходящих через B, ведут из города A в город С?
5 3
2. На вершину горы ведут 5 дорог.
1) Сколькими способами турист может подняться на гору и потом спуститься? 5 5
2) Сколькими способами турист может подняться на гору и потом спуститься,
если подъем и спуск происходят по разным дорогам? 5 4
3. В одном классе 25 учеников, а в другом 24. Сколькими способами можно выбрать:
1) одного ученика на конференцию,
2) двух учеников на олимпиаду,
25 24 49
49 48
2
3) по одному человеку из каждого класса?
25 24
4. Сколькими способами можно указать на шахматной доске 2 квадрата:
1) белый и черный,
32 32
2) произвольного цвета?
64 63
2
9
10.
Набор элементоввыборкой объема
xi1 , xi2 ,..., xim
m из n
из множества
X x1 , x2 ,..., xn
называется
элементов. Выборка называется упорядоченной
(неупорядоченной), если порядок следования элементов в ней задан (не является
существенным). В выборках могут допускаться или не допускаться повторения
элементов.
Упорядоченная выборка
Неупорядоченная выборка
Размещения без повтора
Без повторения
элементов
n!
,m n
m
An n m !
0,
m n
Перестановка Pn An n !
n
С повторением
элементов
Размещения с повтором
m
n
A n
m
Сочетания без повтора
n!
,m n
Cnm m ! n m !
,
0,
m n
Сочетания с повтором
m
n
C Cnm m 1 Cnn m1 1
0
0
Замечание: В случае нулевой выборки принято, что An Cn An C n 1.
0
0
10
11.
25
A 5 5
1. На вершину горы ведут 5 дорог.
1) Сколькими способами турист может подняться на гору и потом спуститься?
2) Сколькими способами турист может подняться на гору и потом спуститься,
5!
2
если подъем и спуск происходят по разным дорогам?
A
5 4
5
(5 2)!
2. В одном классе 25 учеников, а в другом 24. Сколькими способами можно
выбрать:
1) двух учеников на олимпиаду,
49! 49 48
C
2!47!
2
2
49
2) 6 человек для участия в математическом бою (один из них – капитан),
3) по три человека из каждого класса для дежурства в столовой?
5
49 C48
3
3
C25
C24
3. Трое ребят собрали с яблони 40 яблок. Сколькими способами они могут
разделить яблоки между собой, если
40
42!
40
1) все яблоки одинаковые,
C 3 C42
21 41
2!40!
2) все яблоки разные?
40
3
A 340
11
12.
Из колоды, состоящей из 52 карт, выбрали 10 карт.Определить в скольких случаях среди них окажутся:
1) пиковая дама,
10 1
9
1 C52
C
1
51
10 4
6
C52
C
4
48
2) все четыре дамы,
3) все карты одного цвета,
4) все карты одной масти,
10
10
10
C26
C26
или 2 C26
4 C1310
5) ни одного туза,
10
C48
6) ровно один туз,
10 1
9
4 C48
4 C48
7) ровно два туза,
10 2
8
C42 C48
6 C48
8) хотя бы один туз,
10
10
C52
C48
9) не менее двух тузов?
10
10
9
2 8
3 7
4 6
C52
C48
4 C48
или C4 C48 C4 C48 C4 C48
12
13.
Найти все решения в целых неотрицательных числах уравненияx1 x2 ... xk n .
n 5, k 3
1101101
x1 2, x2 2, x3 1
0011111
x1 0, x2 0, x3 5
1100111
x1 2, x2 0, x3 3
k 1
n k 1
C
C
n
n k 1
13
14.
Сколько можно сделать перестановок из n элементов, в которых1) два данные элемента a и b стоят рядом,
n 1 ! A22 2 n 1 !
2) два данные элемента a и b не стоят рядом,
n! A22 n 1 ! n! 2 n 1 !
3) данные три элемента a, b и c не стоят рядом,
n! A33 n 2 ! n ! 6 n 2 !
4) никакие два элемента из элементов a, b и c не стоят рядом,
n! A32 n 1 ! A33 n 2 ! n! 6 n 1 ! 6 n 2 !
5) никакие два элемента из элементов a, b, c и d не стоят рядом?
n! A42 n 1 ! A43 n 2 ! A44 n 3 !
n! 12 n 1 ! 24 n 2 ! 24 n 3 !
14
15.
РазбиенияСовокупность множеств X1 , X 2 ,..., X k ( k 1 ) называется разбиением
множества X , если:
k
1)
X i X , 2) i j X i
X j .
i 1
Разбиения могут быть упорядочены и неупорядочены.
Пример. Пусть X 1,2,3,4,5 .
1) X1 1,2 , X 2 3,4 , X 3 5 ,
2) X1 3,4 , X 2 1,2 , X 3 5 ,
3) X1 2,1 , X 2 5 , X 3 3,4 ,
4) X1 1,2 , X 2 4,5 , X 3 3 .
Если рассматриваются неупорядоченные разбиения, то 1,2 и 3 совпадают.
15
16.
Упорядоченные разбиенияМножество X , X n разбивается на подмножества X1 , X 2 ,..., X k такие,
что X i ni , i 1, k . Количество таких разбиений можно вычислить по формуле:
n1 ,n2 ,...,nk
n
C
n!
.
n1! n2!...nk!
Неупорядоченные разбиения
Множество X , X n разбивается на подмножества, среди которых mi
n
подмножеств с i элементами, причем
m i n . Количество таких разбиений
i 1
i
можно вычислить по формуле.
m1
m2
m3
mn
Cn1,1,...,1,2,2,...,2,3,3,...,3,..., n
n!
.
m2
m3
mn
m1! m2! m3!... mn!
m1! 2! m2! 3! m3!... n ! mn!
16
17.
1. Квадрат 3х3. Сколько разных раскрасок четырьмя цветамитаких, что
1-й цвет – 3 клетки,
2-й цвет – 2 клетки,
3,2,3,1
C9
3-й цвет – 3 клетки,
4-й цвет – 1 клетка.
2. При игре в домино 4 игрока делят поровну 28 костей.
Сколькими способами они могут это сделать?
C
7,7,7,7
28
17
18.
Из 80 человек набирается несколько туристических групп:1) Франция – 20, Англия – 30, Германия – 30,
C8020,30,30
C8020,30,30
2
C 20,20,20,20
2) Франция – 20, Англия – 2 группы по 30 человек,
3) Франция – 4 группы по 20 человек,
4) Франция – 5 групп по 8 человек,
Англия – 4 группы по 10 человек,
80
4!
C808,8,8,8,8,10,10,10,10
5! 4!
5) Франция – 20, Англия – 3 группы по 10 человек,
Германия – 3 группы по 10 человек,
Сколькими способами это можно сделать?
C8020,10,10,10,10,10,10
3! 3!
18
19.
Перестановки с повторениямиСколько существует размещений с повторениями P n1 , n2 ,..., nk
из n элементов, таких, что в выборке ровно
n1 элементов 1-го типа,
n2 элементов 2-го типа,
…
nk элементов k -го типа.
Каждой выборке поставим в соответствие разложение n элементов
(номеров позиций) по k ящикам (типам элементов):
в 1-й ящик – элементы 1-го типа,
во 2-й ящик – элементы 2-го типа,
…
в k ящик – элементы k типа.
Получим разбиение n –элементного множества на k подмножеств
с мощностями n1 , n2 ,..., nk . Следовательно, количество таких перестановок
n1 ,n2 ,...,nk
n
C
19
20.
12.1) У мамы 2 яблока и 3 груши. Сколькими способами она может
2,3
выдавать по одному фрукту в течение 5 дней?
C5
2) У мамы 2 яблока, 3 груши и 4 апельсина. Сколькими способами она
может выдавать по одному фрукту в течение 9 дней?
2,3,4
C9
3) У мамы 2 яблока, 3 груши и 4 апельсина. Сколькими способами она
может выдавать не более чем по одному фрукту в течение 12 дней?
C122,3,4,3 или C129 C92,3,4
13.Сколько различных слов (без смысла) можно получить, переставляя
буквы слова «математика».
C102,3,2,1,1,1
20
21.
Полиномиальная формула... xkk
x1 x22 ...
nn
nn11,n,n22,...,
,...,nnkk nn11 nn22
nn
11 22
C
C
nn11 nn22 ...
...nnkk nn
nnk k
kk .
xx xx ...
...xx
x1 x2 ... xk x1 x2 ... xk x1 x2 ... xk ... x1 x2 ... xk
n
1
2
n
Пусть A 1,2,3,..., n – множество номеров скобок.
n
n
n
Каждому многочлену x1 1 x2 2 ...xk k поставим в соответствие разбиение
множества
A на подмножества A1 , A2 ,..., Ak , где Ai множество номеров
скобок из которых брали слагаемое xi .
nn11 nn22
11 22
nnkk
kk будет
Тогда количество одинаковых слагаемых x x ...x
Cnn1 ,n2 ,...,nk.
21
22.
Круглый столСколькими способами n человек могут сесть за круглый стол.
комплексный обед в
столовой на перемене
новогодний вечер в
дорогом ресторане
без ограничений
n! n 1 !
2
2n
2
1n !
a и b должны сидеть
2 n n 2 !
5 n 2 !
2n
2 n 3 n 2 !
2n n 3 6!
n 3 !
2n
2 n 4 n 3 !
рядом
соседями c должны
быть a и b
22
23.
Свойства сочетаний2. Cnk Cnn k
1. Cn0 Cnn 1
4. Cnk Cnk 1 Cnk 1
n
n
3. Cnk 2n
5. 1 Cnk 0
k 0
k 0
n
k 0
1 m C2mm , n 2m,
7. 1 C
0, n 2m 1.
k 0
C
6. C
k 2
n
n
n
2n
m
m
k 0
k 0
8. Cnk k Cnn k Cnm 2
s
10. C C
k 0
n
k
m
s k
n
C
s
m n
k 2
n
k
m
9. 1 Cnk 1 Cnm 1 , m n
k
m
k o
n
n
, s m n 11. C
12. k Cnk x k 1 n (1 x)n 1
k 1
k
k 1
2k
2n
C22nk 1 2n 1
k 1
x 1 1
C x
13.
n 1
k 0 k 1
n
k
n
k 1
n 1
23
24.
Комбинаторные доказательства1. Cn0 Cnn 1
Cn0 – выбрать 0 элементов, Cnn – выбрать все элементы.
2. Cnk Cnn k
Cnk , – выбрать k элементов, Cnk , – выбрать n k элементов.
3. Cnk Cnk 1 Cnk 1
Cnk 1 , – из n 1 элемента выбрать k элементов,
Cnk – из n 1 элемента выбрать k элементов так, чтобы среди них не
было элемента a ,
Cnk 1 – из n 1 элемента выбрать k элементов так, чтобы среди них
был элемент a .
24
25.
mm
8. C
k 0
k
n k
Cnn k Cnm 2
k 0
Рассмотрим m –сочетания с повторениями, составленные из
элементов n 2 типов. Количество таких сочетаний равно
m
m
mm
C
C
Cnn 22 Cnn mm 11 .
Разобьем все эти сочетания на классы, отнеся к i –му классу
сочетания, которые содержат ровно i элементов первого типа.
Количество сочетаний для i -го класса определяется формулой
C mn i2 1 Cnm 1i .
Тогда
общее
повторением из элементов
следующим образом:
m
m
n 2
C
C
i 0
m i
n 1
m
C
i 0
m i
n 1 m i 1
количество
n 2
m
C
i 0
m –сочетаний
с
типов можно вычислить
m i
n m i
m
m
k : m i C
Cnnkk kk .
00
kk
25
26.
Аналитические доказательства1. Cn0
n!
n!
1, Cnn
1
0!(n 0)!
n!(n n)!
2. Cnk
n!
n!
, Cnn k
Cnk Cnn k
k ! n k !
n k !k !
3. Cnk Cnk 1
n!
n!
k ! n k ! k 1 ! n k 1 !
1
n 1 !
n!
1
Cnk 1
k 1 ! n k ! k n k 1 k 1 ! n k 1 !
n
4. 2 1 1 C 1 1
n
n
k
n
k 0
k
n
n k
n
Cnk
k 0
5. 0 1 1 C 1 1
n
n
k 0
k
n
k
n k
n
1 Cnk
k 0
k
26
27.
nC
6. C
k 0
k 2
n
n
2n
Рассмотрим тождество 1 x 1 x 1 x . Коэффициенты
n
n
2n
при x n в левой и правой части тождества должны совпадать.
1 x
2n
2n
C2kn x k ... C2nn x n ...
k 0
1 x
n 2
2
k k
0 0
1 1
2 2
n n 2
Cn x Cn x Cn x Cn x ... Cn x
k 0
n
Cn0 x 0 Cn1 x1 Cn2 x 2 ... Cnn 2 x n 2 Cnn 1 x n 1 Cnn x n
Cn0 x 0 Cn1 x1 Cn2 x 2 ... Cnn 2 x n 2 Cnn 1 x n 1 Cnn x n
... Cn0Cnn Cn1Cnn 1 Cn2Cnn 2 ...Cnn 2Cn2 Cnn 1Cn1 CnnCn0 x n ...
C C
k
n
n k
n
... C x ...
n
k 0
k 2 n
n
27
28.
1 m C2mm , n 2m,7. 1 C
0, n 2m 1.
k 0
n
k
k 2
n
1 x 1 x 1 x . Коэффициенты
n
Рассмотрим тождество
2 n
n
при x n в левой и правой части тождества должны совпадать.
1 x 1 x
n
n
C x C x C x ... 1 Cnn x n Cn0 x0 Cn1 x1 Cn2 x 2 ... Cnn x n
0 0
n
1 1
n
n
2 2
n
... Cn0Cnn Cn1Cnn 1 Cn2Cnn 2 ... 1 CnnCn0 x n ... Cnk Cnn k
n
... 1 C x n ...
n
k
k 0
1. n 2m 1. Разложение 1 x
k 2
n
не содержит нечетных степеней, поэтому
2 n
n
коэффициент при x должен быть равен 0.
2. n 2m :
1 x ... 1 C x ...
2 n
m
m
2m
2m
28
29.
s10. Cnk Cms k Cms n , s n m
k 0
Рассмотрим тождество
1 x 1 x 1 x
m
n
m n
.
Коэффициенты при x s в левой и правой части тождества должны
совпадать.
1 x
m n
m n
Cmk n x k ... Cms n x s ...
k 0
m k k n k k
1 x 1 x Cm x Cn x
k 0
k 0
m
n
Cm0 x 0 Cm1 x1 Cm2 x 2 ... Cmm x m Cn0 x 0 Cn1 x1 Cn2 x 2 ... Cnn x n
... Cm0 Cns Cm1 Cns 1 Cm2 Cns 2 ... Cms Cn0 x s ... ... Cnk Cms k x s ...
s
k 0
29
30.
n12. k Cnk x k 1 n (1 x)n 1
k 1
n
(1 x) n Cnk x k ,
k 0
n
n
(1 x)n n(1 x)n 1 , Cnk xk kCnk xk 1 .
k 0
k 1
x 1 1
C x
13.
n 1
k 0 k 1
n
k
n
n 1
k 1
n 1 !
Cnk
Cnk 11
n!
.
k 1 k 1 k ! n k ! n 1 k 1 ! n k ! n 1
Cnk x k 1
1 n k 1 k 1
Cn 1 x l : k 1
n 1 k 0
k 0 k 1
n
1 x 1
1
1
l
l
l
l
0
0
Cn 1 x
Cn 1 x Cn 1 x
n 1 l 1
n 1 l 0
n 1
30
n 1
n 1
n 1






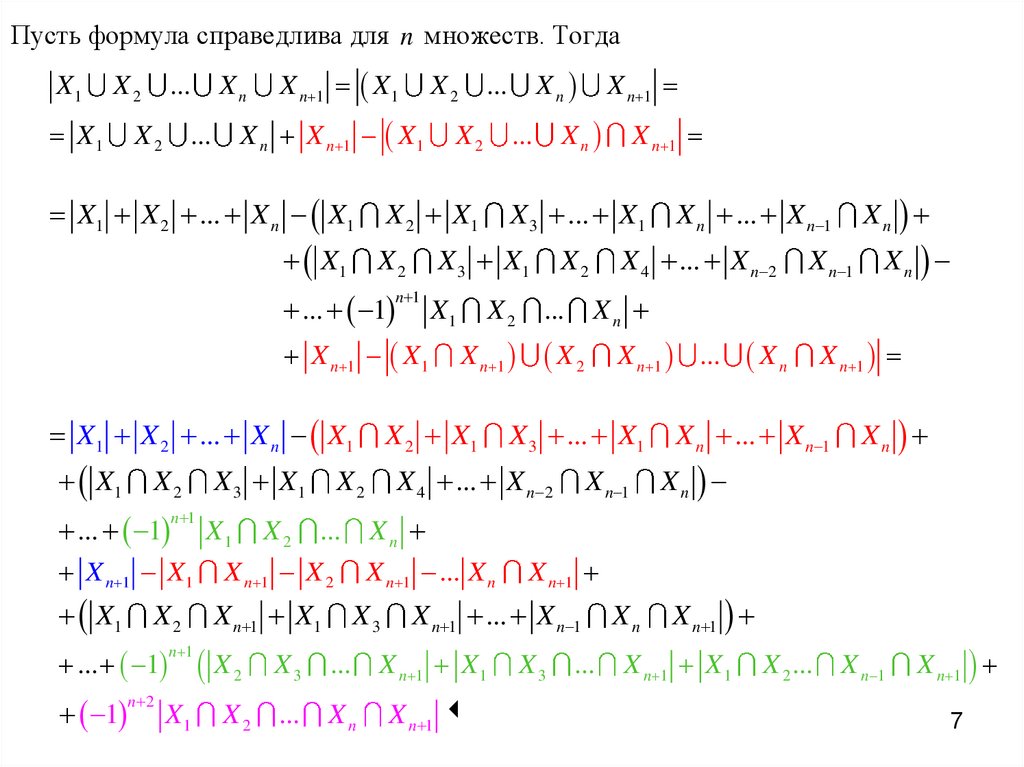






















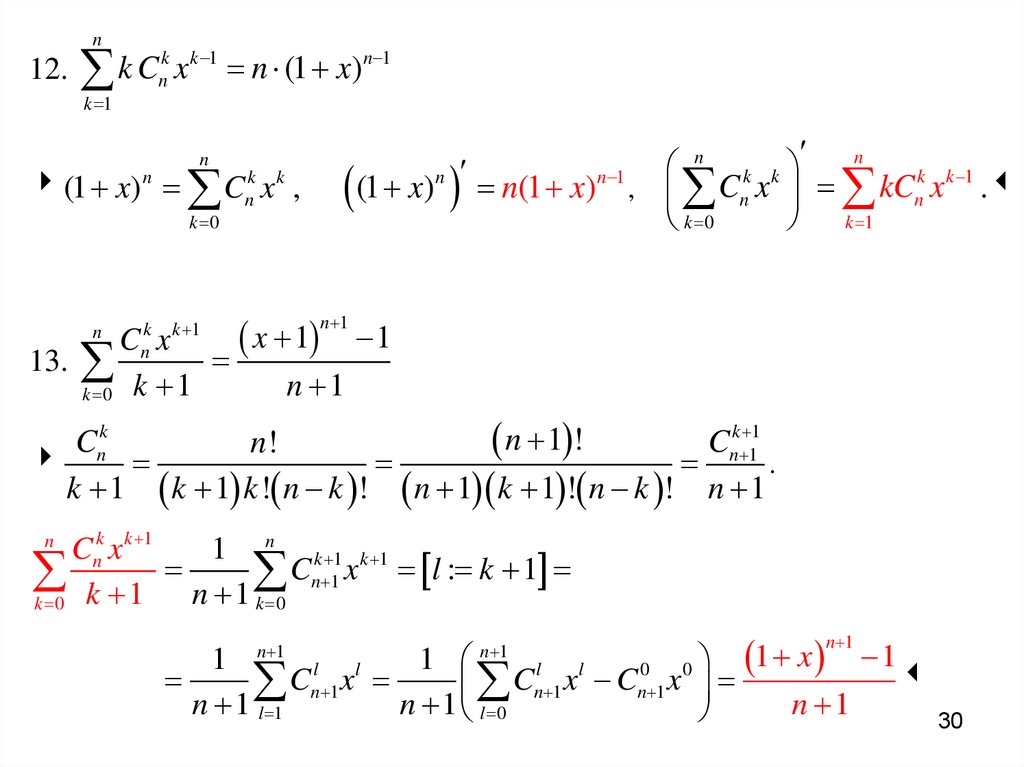
 Математика
Математика








