Похожие презентации:
Комбинаторика
1.
КомбинаторикаВиленкин Н.Я. Комбинаторика.
Виленкин Н.Я. Популярная комбинаторика.
Нефедов В.Н., Осипова В.А. Курс дискретной математики.
Липский В. Комбинаторика для программистов.
Андерсон Джеймс А. Дискретная математика и
комбинаторика.
1
2.
Задачи комбинаторики – пересчет и перечисление элементов вконечных множествах.
Задача пересчета – сколько элементов, принадлежащих заданному
конечному множеству, обладают заданным свойством.
Задача перечисления – выделение из конечного множества всех
элементов, удовлетворяющих заданному свойству.
2
3.
Пусть X n . Тогда объект x может быть выбран из множества X nспособами.
Правило суммы. Если объект x может быть выбран m способами, а
объект y – другими n способами, то выбор «либо x , либо y » можно
сделать m n способами.
Следствие. Пусть X 1 , X 2 , …, X k – попарно непересекающиеся
множества, тогда
k
i 1
k
Xi Xi .
i 1
Правило произведения. Если объект x может быть выбран m
способами и после каждого из таких выборов объект y в свою очередь
может быть выбран n способами, то выбор упорядоченной пары x, y ,
можно сделать mn способами.
3
4.
Правило произведения. Если объект x может быть выбран m способамии после каждого из таких выборов объект y в свою очередь может быть
выбран n способами, то выбор упорядоченной пары
x, y , можно сделать
mn способами.
Пусть объект x выбирается из множества X a1, a2 ,..., an . Обозначим
через X i – множество пар x, y при x ai . Тогда множества X i попарно не
пересекаются и X i n i 1, m . Следовательно,
m
i 1
m
m
i 1
i 1
X i X i n mn .
Следствие. Если объект x1 может быть выбран n1 способами, после чего
объект x2 в свою очередь может быть выбран n2 способами и i 2, m 1 ,
после выбора объектов x1 , x2 ,..., xi объект xi 1 может быть выбран ni 1
способами, то выбор упорядоченной последовательности из m объектов
x1 , x2 ,..., xm можно сделать n1n2 ...nm способами.
4
5.
Формула включений и исключений.Пусть X i – конечные множества, i 1,2,..., n , n 2 . Тогда X1
X2
...
Xn
X 1 X 2 ... X n X 1 X 2 X 1 X 3 ... X 1 X n ... X n 1 X n
n 1
X 1 X 2 X 3 X 1 X 2 X 4 ... X n 2 X n 1 X n ... 1 X 1 X 2 ...
Xn
.
Докажем методом математической индукции.
1. n 2 . Если X 1
X 2 , то X1
X 2 X1 X 2 . Если X 1
X 1 X 2 каждый элемент множества X 1
X1
X 2 , то в сумме
X 2 посчитан 2 раза, а значит,
X 2 X1 X 2 X1
X2 .
5
6.
Пусть формула справедлива для n множеств. ТогдаX1
X2
X1
...
X2
Xn
X n 1 X 1
X2
X n X n 1 X 1
...
X1 X 2 ... X n X1
X1
n 1
X1 X 2 ... X n X1
X2
X 3 X1
X1
X n 1
X 3 ... X1
X2
X n 1
X 2 X1
... 1 X1 X 2 ... X n
X n 1 X1 X n 1 X 2 X n 1 ... X n
Xn
X n ... X n 1
X 4 ... X n 2
X2
X n 1
Xn
Xn
...
X2
X n 1 ...
X 3 ... X1
X 4 ... X n 2
X2
X n 1
Xn
...
X 3 X1
X2
X n 1 X 1
X1
X2
X 2 X1
... 1
Xn
...
X n 1
Xn
X n 1
X n ... X n 1
Xn
Xn
n 1
X1
X2
... 1
1
n 2
n 1
X1
X n 1 X1
X
X3
X n 1
X n 1 ... X n 1
2
X3
...
X n 1 X 1
X2
...
Xn
X n 1
X3
...
Xn
X n 1
X n 1 X 1
X 2 ...
X n 1
X n 1
6
7.
ПримерВ НИИ работает несколько человек, причем все они знают
хотя бы по одному языку:
англ. – 6,
англ. и нем. – 4,
франц. – 7,
англ. и франц. – 2,
нем. – 6,
нем. и франц. – 3,
1) Сколько человек в НИИ?
все три языка – 1.
6 + 7 + 6 – (4 + 2 + 3) + 1 = 11
2) Сколько человек знают только английский?
3) Сколько человек знают только французский?
6 – (4 + 2) + 1 = 1
7 – (2 + 3) + 1 = 3
7
8.
1. Из города A в город B ведут пять дорог, а из города B в город С – три. Сколько путей,проходящих через B, ведут из города A в город С?
5 3
2. На вершину горы ведут 5 дорог.
5 5
1) Сколькими способами турист может подняться на гору и потом спуститься?
2) Сколькими способами турист может подняться на гору и потом спуститься, если
подъем и спуск происходят по разным дорогам?
5 4
3. В одном классе 25 учеников, а в другом 24. Сколькими способами можно выбрать:
1) одного ученика на конференцию,
25 24 49
2) двух учеников на олимпиаду,
49 48
2
3) по одному человеку из каждого класса?
25 24
4. Сколькими способами можно указать на шахматной доске 2 квадрата:
1) белый и черный,
32 32
2) произвольного цвета?
64 63
2
8
9.
Набор элементов xi1 , xi2 ,..., xim из множества X x1, x2 ,..., xn называется выборкой объема mиз n элементов.
Выборка называется упорядоченной, если порядок следования элементов в ней задан. Если
порядок следования элементов в выборке не является существенным, то выборка называется
неупорядоченной.
В выборках могут допускаться или не допускаться повторения элементов.
Перестановкой называется упорядоченная выборка без повтора объема n из n элементов.
Упорядоченная выборка
Без повторения
элементов
Размещения без повтора
n!
, m n
Anm n m !
0, m n
Перестановки Pn Ann n!
С повторением
элементов
Размещения с повтором
m
An n m
Неупорядоченная выборка
Сочетания без повтора
n!
,m n
m
Cn m! n m !
,
0, m n
Сочетания с повтором
m
C n Cnm m 1 Cnn m1 1
0
0
Замечание: В случае нулевой выборки принято, что An0 Cn0 An C n 1 .
9
10.
1. На вершину горы ведут 5 дорог.1) Сколькими способами турист может подняться на гору и потом спуститься?
2
5
A 5 5
2) Сколькими способами турист может подняться на гору и потом спуститься, если
подъем и спуск происходят по разным дорогам?
5!
A52
5 4
(5 2)!
3. В одном классе 25 учеников, а в другом 24. Сколькими способами можно выбрать:
49!
49 48
2!47!
2
2) 6 человек для участия в математическом бою (один из них – капитан),
2
C49
1) двух учеников на олимпиаду,
3) по три человека из каждого класса для дежурства в столовой?
5
49 C48
3
3
C25
C24
5. Трое ребят собрали с яблони 40 яблок. Сколькими способами они могут разделить
яблоки между собой, если
1) все яблоки одинаковые,
2) все яблоки разные?
42!
C C
21 41
2!40!
40
A3 340
40
3
40
42
10
11.
6. Из колоды, состоящей из 52 карт, выбрали 10 карт.Определить в скольких случаях среди них окажутся:
1) пиковая дама,
10 1
9
1 C52
C
1
51
2) все четыре дамы,
10 4
6
C52
C
4
48
3) все карты одного цвета,
4) все карты одной масти,
5) ни одного туза,
10
10
10
C26
C26
или 2 C26
4 C1310
10
C48
6) ровно один туз,
10 1
9
4 C48
4 C48
7) ровно два туза,
10 2
8
C42 C48
6 C48
8) хотя бы один туз,
9) не менее двух тузов?
10
10
C52
C48
10
10
9
2 8
3 7
4 6
C52
C48
4 C48
или C4 C48 C4 C48 C4 C48
11
12.
7. Найти все решения в целых неотрицательных числах уравненияx1 x2 ... xk n .
n 5, k 3
1101101
x1 2, x2 2, x3 1
0011111
x1 0, x2 0, x3 5
1100111
x1 2, x2 0, x3 3
k 1
n k 1
C
C
n
n k 1
12
13.
8. Сколько можно сделать перестановок из n элементов, в которых1) два данные элемента a и b стоят рядом,
n 1 ! A22 2 n 1 !
2) два данные элемента a и b не стоят рядом,
n! A22 n 1 ! n! 2 n 1 !
3) данные три элемента a, b и c не стоят рядом,
n! A33 n 2 ! n! 6 n 2 !
4) никакие два элемента из элементов a, b и c не стоят рядом,
n! A32 n 1 ! A33 n 2 ! n! 6 n 1 ! 6 n 2 !
5) никакие два элемента из элементов a, b, c и d не стоят рядом,
n! A42 n 1 ! A43 n 2 ! A44 n 3 !
n! 12 n 1 ! 24 n 2 ! 24 n 3 !
13
14.
РазбиенияСовокупность множеств
k
множества X , если
1)
X1 , X 2 ,..., X k
( k 1 ) называется разбиением
X i X , 2) i j X i
X j .
i 1
Разбиения могут быть упорядочены и неупорядочены.
Пример. Пусть X 1,2,3,4,5 .
1) X1 1,2 , X 2 3,4 , X 3 5 ,
2) X1 3,4 , X 2 1,2 , X 3 5 ,
3) X1 2,1 , X 2 5 , X 3 3,4 ,
4) X1 1,2 , X 2 4,5 , X 3 3 .
Если рассматриваются неупорядоченные разбиения, то 1,2 и 3 совпадают.
14
15.
Упорядоченные разбиенияМножество X , X n разбивается на подмножества X1 , X 2 ,..., X k такие, что
X i ni , i 1, k . Количество таких разбиений можно вычислить по формуле:
C
n1 ,n2 ,...,nk
n
n!
.
n1! n2!...nk!
Неупорядоченные разбиения
Множество
X,
X n разбивается на подмножества, среди которых mi
n
подмножеств с i элементами, причем
m i n . Количество таких разбиений можно
i 1
i
вычислить по формуле.
m1
m2
m3
mn
Cn1,1,...,1,2,2,...,2,3,3,...,3,..., n
n!
.
m2
m3
mn
m1!m2!m3!... mn!
m1! 2! m2! 3! m3!... n! mn!15
16.
9. Квадрат 3х3. Сколько разных раскрасок четырьмя цветамитаких, что
1-й цвет – 3 клетки,
2-й цвет – 2 клетки,
3,2,3,1
C9
3-й цвет – 3 клетки,
4-й цвет – 1 клетка.
10. При игре в домино 4 игрока делят поровну 28 костей.
Сколькими способами они могут это сделать?
C
7,7,7,7
28
16
17.
10.Из 80 человек набирается несколько туристических группы:1) Франция – 20, Англия – 30, Германия – 30,
C8020,30,30
2) Франция – 20, Англия – 2 группы по 30 человек,
C8020,20,20,20
4!
3) Франция – 4 группы по 20 человек,
4) Франция – 5 групп по 8 человек,
Англия – 4 группы по 10 человек,
C8020,30,30
2
C808,8,8,8,8,10,10,10,10
5! 4!
5) Франция – 20, Англия – 3 группы по 10 человек,
Германия – 3 группы по 10 человек,
C8020,10,10,10,10,10,10
3! 3!
Сколькими способами это можно сделать?
17
18.
Перестановки с повторениямиСколько существует размещений с повторениями P n1 , n2 ,..., nk из
n элементов, таких, что в выборке ровно
n1 элементов 1-го типа,
n2 элементов 2-го типа,
…
nk элементов k -го типа.
Каждой выборке поставим в соответствие разложение n элементов
(номеров позиций) по k ящикам (типам элементов):
в 1-й ящик – элементы 1-го типа,
во 2-й ящик – элементы 2-го типа,
…
в k ящик – элементы k типа.
Получим разбиение n –элементного множества на k подмножеств с
мощностями n1 , n2 ,..., nk . Следовательно, количество таких перестановок
n1 ,n1 ,...,nk
.
n
C
18
19.
12.1) У мамы 2 яблока и 3 груши. Сколькими способами она может
выдавать по одному фрукту в течение 5 дней?
2,3
C5
2) У мамы 2 яблока, 3 груши и 4 апельсина. Сколькими способами она
может выдавать по одному фрукту в течение 9 дней?
2,3,4
C9
3) У мамы 2 яблока, 3 груши и 4 апельсина. Сколькими способами она
может выдавать не более чем по одному фрукту в течение 12 дней?
9
12
2,3,4
9
C C
13.Сколько различных слов (без смысла) можно получить, переставляя
буквы слова «математика».
2,3,2,1,1,1
10
C
19
20.
Полиномиальная формула... xkk
x1 x22 ...
nn
nn11,n,n22,...,
nnk k
,...,nnkk nn11 nn22
C
x
x
...
x
Cnn
x11 x22 ...xkk .
nn11 nn22 ...
...nnkk nn
x1 x2 ... xk x1 x2 ... xk x1 x2 ... xk ... x1 x2 ... xk
n
1
2
n
Пусть A 1,2,3,..., n – множество номеров скобок.
n
n
n
Каждому многочлену x1 1 x2 2 ...xk k поставим в соответствие разбиение
множества
A на подмножества A1 , A2 ,..., Ak , где Ai множество номеров
скобок из которых брали слагаемое xi .
n , n2 ,...,nk
nn
nn nn
1
Тогда количество одинаковых слагаемых x1111 x2222 ...xkkkk будет Cn
.
20
21.
Круглый столСколькими способами n человек могут сесть за круглый стол.
комплексный обед в
столовой на перемене
новогодний вечер в
дорогом ресторане
без ограничений
n! n 1 !
2
2n
2
1n !
a и b должны сидеть
2 n n 2 !
5 n 2 !
2n
2 n 3 n 2 !
2n n 3 6!
n 3 !
2n
2 n 4 n 3 !
рядом
соседями c должны
быть a и b
22
22.
Свойства сочетаний2. Cnk Cnn k
1. Cn0 Cnn 1
4. Cnk Cnk 1 Cnk 1
n
n
3.
k
n
C
2
n
5.
6.
C
k 0
k 2
n
C
m
8.
C C
k 0
s k
n
n
12.
k C
k 1
m
9.
k 0
k
m
k
n
x
C
k 1
s
m n
k 2
n
k
k 0
Cnk k Cnn k Cnm 2
s
10.
7.
m
k 0
1 C
n
n
2n
k
k 0
k 0
n
k
1
C
n 0
n (1 x)
1 Cnk 1 Cnm 1, m n
k
m
k o
, s m n 11.
n
n
C
k 1
n 1
1 m C2mm , n 2m,
0, n 2m 1.
n
2k
2n
k
n
C22nk 1 2n 1
k 1
k 1
C x
13.
k 0 k 1
x 1
n 1
1
n 1
23
23.
Комбинаторные доказательства1. Cn0 Cnn 1
Cn0 – выбрать 0 элементов, Cnn – выбрать все элементы.
2. Cnk Cnn k
Cnk , – выбрать k элементов, Cnk , – выбрать n k элементов.
3. Cnk Cnk 1 Cnk 1
Cnk 1 , – из n 1 элемента выбрать k элементов,
Cnk – из n 1 элемента выбрать k элементов так, чтобы среди них не
было элемента a ,
Cnk 1 – из n 1 элемента выбрать k элементов так, чтобы среди них
был элемент a .
24
24.
m8.
m
C
k 0
k
n k
Cnn k Cnm 2
k 0
Рассмотрим m –сочетания с повторениями, составленные из
элементов n 2 типов. Количество таких сочетаний равно
Cnmnm 22 CCnmnm mm 11 .
C
Разобьем все эти сочетания на классы, отнеся к i –му классу
сочетания, которые содержат ровно i элементов первого типа.
Количество сочетаний для i -го класса определяется формулой
C mn i2 1 Cnm 1i .
Тогда
общее
повторением из элементов
следующим образом:
mm
nn 22
C
C
количество
n 2
типов
m –сочетаний
с
можно вычислить
m
m
m
m
m
i 0
i 0
i 0
kk 00
k
Cnm 1i C mn 1i m i 1 Cnm mi i k : m i Cnnk kk .
25
25.
Аналитические доказательства1. Cn0
n!
n!
1, Cnn
1
0!(n 0)!
n!(n n)!
2. Cnk
n!
n!
, Cnn k
Cnk Cnn k
k ! n k !
n k !k !
3. Cnk Cnk 1
n!
n!
k ! n k ! k 1 ! n k 1 !
1
n 1 !
n!
1
Cnk 1
k 1 ! n k ! k n k 1 k 1 ! n k 1 !
n
4. 2 1 1 C 1 1
n
n
k
n
k 0
k
n
n k
n
Cnk
k 0
5. 0 1 1 C 1 1
n
n
k 0
k
n
k
n k
n
1 Cnk
k 0
k
26
26.
Cn
6.
k 0
k 2
n
C2nn
Рассмотрим тождество 1 x 1 x 1 x . Коэффициенты
n
n
2n
при x n в левой и правой части тождества должны совпадать.
1 x
2n
2n
C2kn x k ... C2nn x n ...
k 0
1 x
n 2
2
k k
0 0
1 1
2 2
n n 2
Cn x Cn x Cn x Cn x ... Cn x
k 0
n
Cn0 x 0 Cn1 x1 Cn2 x 2 ... Cnn 2 x n 2 Cnn 1 x n 1 Cnn x n
Cn0 x 0 Cn1 x1 Cn2 x 2 ... Cnn 2 x n 2 Cnn 1 x n 1 Cnn x n
... Cn0Cnn Cn1Cnn 1 Cn2Cnn 2 ...Cnn 2Cn2 Cnn 1Cn1 CnnCn0 x n ...
C C
k
n
n k
n
... C
n
k 0
x
k 2 n
n
...
27
27.
1 Cn
7.
k
k 0
k 2
n
1 m C2mm , n 2m,
0, n 2m 1.
1 x 1 x
n
Рассмотрим тождество
n
1 x
.
2 n
Коэффициенты
при x n в левой и правой части тождества должны совпадать.
1 x 1 x
n
n
C x C x C x ... 1 Cnn x n Cn0 x0 Cn1 x1 Cn2 x 2 ... Cnn x n
0 0
n
1 1
n
n
2 2
n
... Cn0Cnn Cn1Cnn 1 Cn2Cnn 2 ... 1 CnnCn0 x n ... Cnk Cnn k
n
... 1 C
n
k
k 0
1. n 2m 1. Разложение 1 x
2 n
x
k 2
n
n
...
не содержит нечетных степеней, поэтому
n
коэффициент при x должен быть равен 0.
2. n 2m :
1 x
2 n
... 1 C2mm x 2 m ...
m
28
28.
s10.
k s k
s
C
C
C
n m m n , s n m
k 0
Рассмотрим тождество
1 x 1 x
m
n
1 x
m n
.
Коэффициенты при x s в левой и правой части тождества должны
совпадать.
1 x
m n
m n
Cmk n x k ... Cms n x s ...
k 0
1 x 1 x
m
n
m k k n k k
Cm x Cn x
k 0
k 0
Cm0 x 0 Cm1 x1 Cm2 x 2 ... Cmm x m Cn0 x 0 Cn1 x1 Cn2 x 2 ... Cnn x n
... Cm0 Cns Cm1 Cns 1 Cm2 Cns 2 ... Cms Cn0 x s ... ... Cnk Cms k x s ...
s
k 0
29
29.
n12.
k k 1
n 1
k
C
x
n
(1
x
)
n
k 1
n
(1 x)n Cnk x k ,
k 0
n
n
(1 x)n n(1 x)n 1 , Cnk x k kCnk x k 1 .
k 0
k 1
x 1 1
C x
13.
n 1
k 0 k 1
n
k
n
n 1
k 1
n 1 !
Cnk
Cnk 11
n!
.
k 1 k 1 k ! n k ! n 1 k 1 ! n k ! n 1
Cnk x k 1
1 n k 1 k 1
Cn 1 x l : k 1
n 1 k 0
k 0 k 1
n
1
1
l
l
l
l
0
0
C
x
C
x
C
x
n 1
n 1
n 1
n 1 l 1
n 1 l 0
n 1
n 1
1 x
n 1
n 1
1
30




























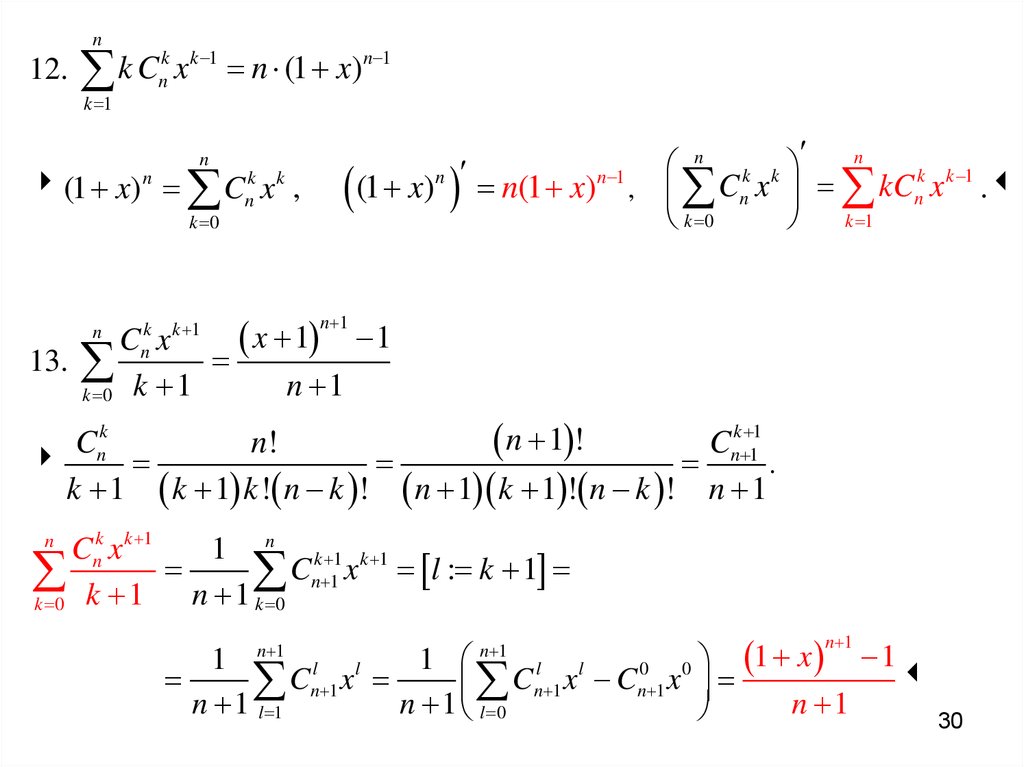
 Математика
Математика








