Применение теоремы Менелая при решении задач

1.

Муниципальное бюджетное общеобразовательное учреждение города Кургана «Гимназия №47»
Индивидуальный проект
«Применение теоремы Менелая при решении
задач»
Направление: «Математика»
А В Т О Р П Р О Е К ТА :
ГРЕКОВ ДМИТРИЙ ЕВГЕНЬЕВИЧ,
У Ч Е Н И К 1 0 « Г » К Л АС СА М Б ОУ Г О Р ОД А
К У Р ГА Н А « Г И М Н А З И Я № 4 7 »
г. Курган
2023
Р У К О В ОД И Т Е Л Ь П Р О Е К ТА :
А Б РА М О ВА ОЛ Ь ГА С Е Р Г Е Е В Н А ,
У Ч И Т Е Л Ь М АТ Е М АТ И К И М Б ОУ Г О Р ОД А
К У Р ГА Н А « Г И М Н А З И Я № 4 7 »

2.

Введение:
Актуальность – теорема Менелая является классической теоремой аффинной геометрии. Задачи на ее применение могут
встретится не только в школьном учебнике, но и на едином государственном экзамене или на математической олимпиаде самой
разной сложности и уровня.
Цель работы – составление материала, состоящего из теоретической и практической части и нацеленного на помощь учащимся в
изучение темы «Теорема Менелая» и смежным с ней теорем и для последующего усовершенствования навыков решения
геометрических задач.
Задачи:
1. Собрать и изучить материал о теореме, воспользовавшись различными источниками информации;
2. Сформулировать и предоставить доказательство правдивости условия теоремы;
3. Рассмотреть способы применения теоремы Менелая при решении задач и доказательстве других теорем;
4. Сделать подборку достаточного количества задач для отработки и повышения навыков применения этой теоремы.
Объект исследования – теорема Менелая.
Предмет исследования – практическое применение теоремы Менелая.

3.

Теоретическая часть

4.

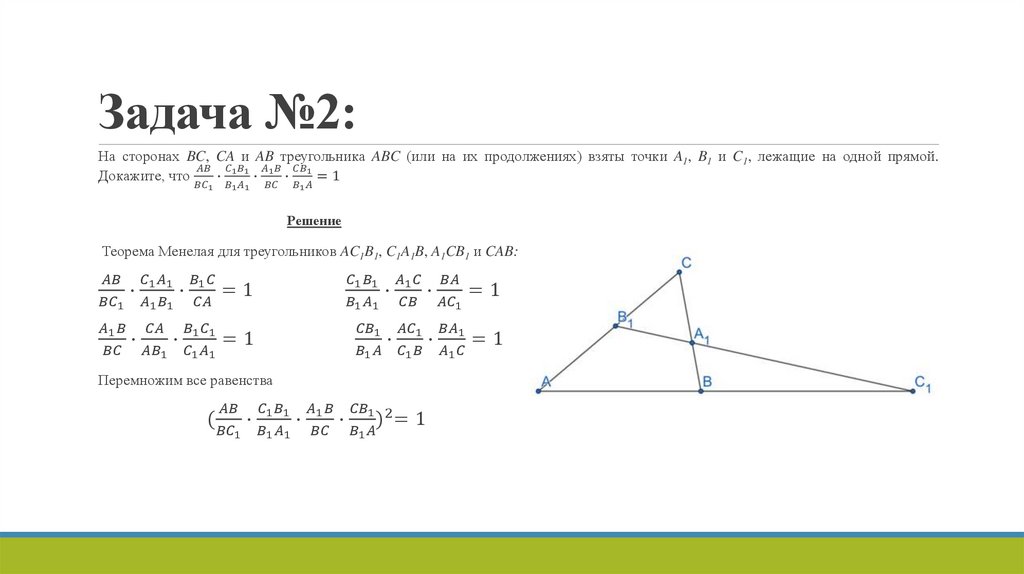
Условие теоремы:
Если точки A1, B1 и C1 лежат соответственно на сторонах BC, AC и AB треугольника ABC или на их продолжения, то они лежат
на одной прямой тогда и только тогда, когда: