Похожие презентации:
Прямоугольный треугольник. Урок 92
1.
2.
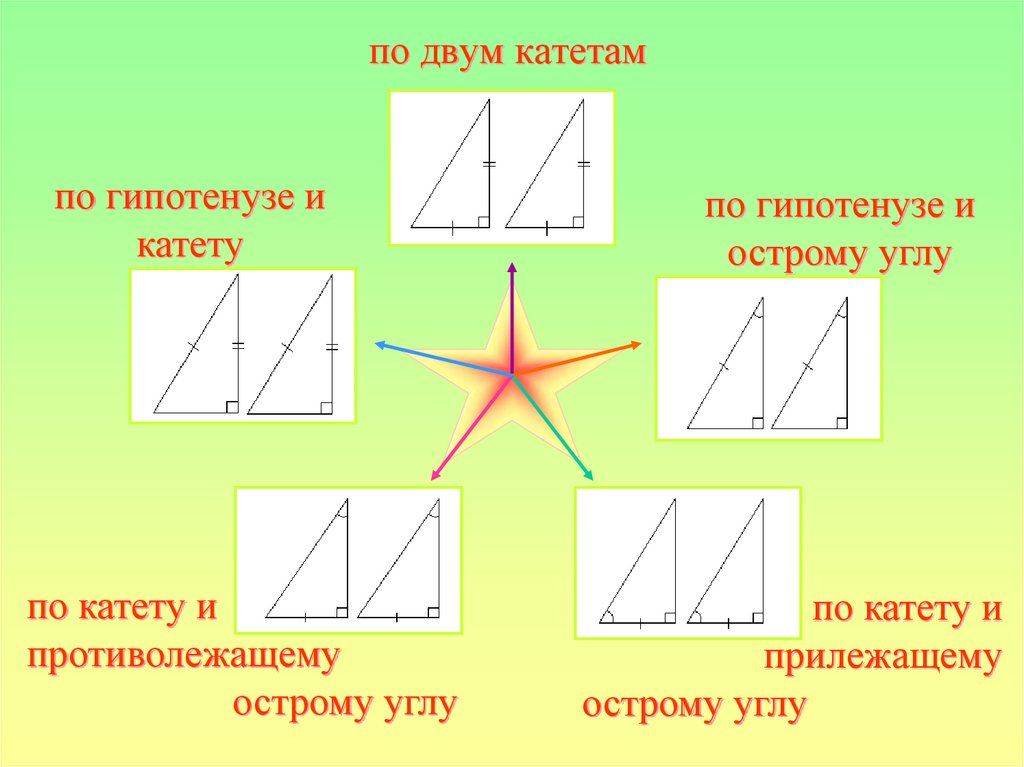
по двум катетампо гипотенузе и
катету
по катету и
противолежащему
острому углу
по гипотенузе и
острому углу
по катету и
прилежащему
острому углу
3.
Выбери правильное завершение определения.Катетом называется…
Любая сторона треугольника;
Сторона, лежащая против
прямого угла треугольника;
Перпендикуляр из вершины угла
на противолежащую сторону;
Сторона, примыкающая к
вершине прямого угла.
4.
Выбери правильное завершение определения.Гипотенузой называется…
Любая сторона треугольника;
Сторона, лежащая против
прямого угла треугольника;
Перпендикуляр из вершины угла
на противолежащую сторону;
Сторона, примыкающая к
вершине прямого угла.
5.
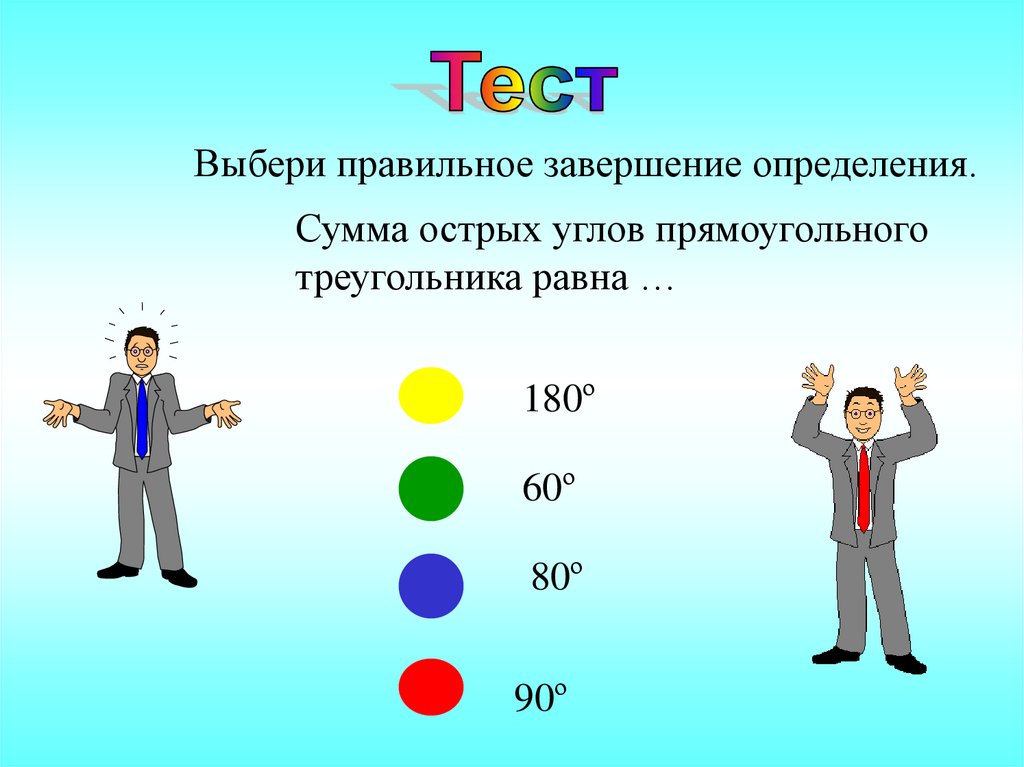
Выбери правильное завершение определения.Сумма острых углов прямоугольного
треугольника равна …
180º
60º
80º
90º
6.
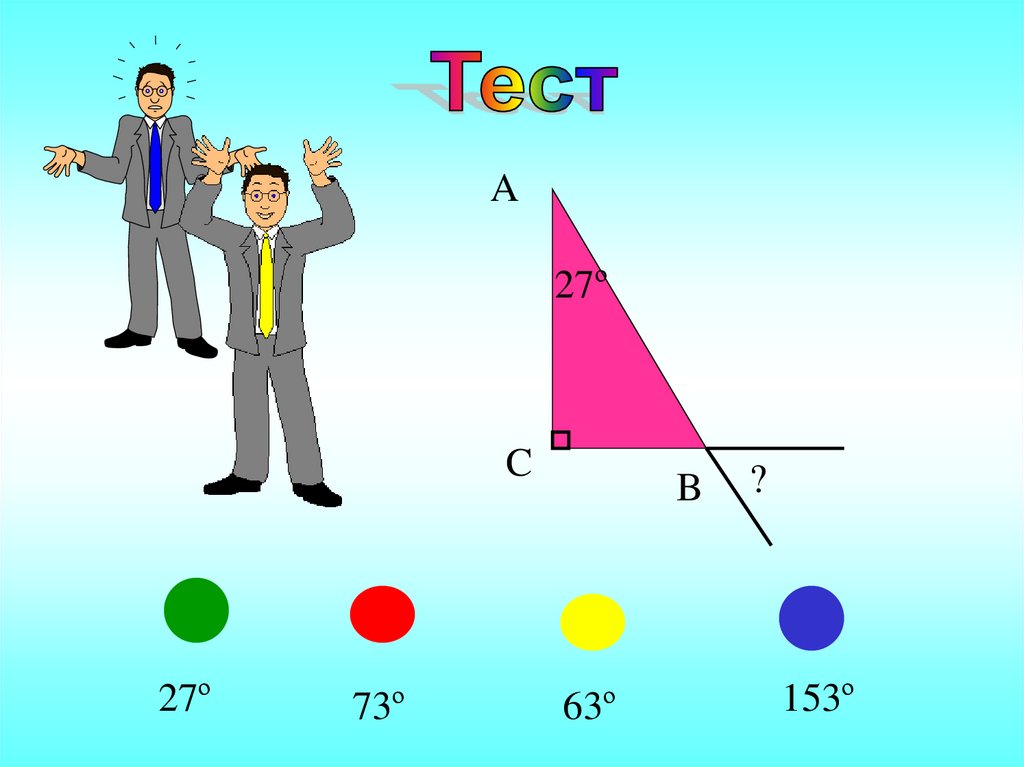
A27º
C
27º
73º
B
63º
?
153º
7.
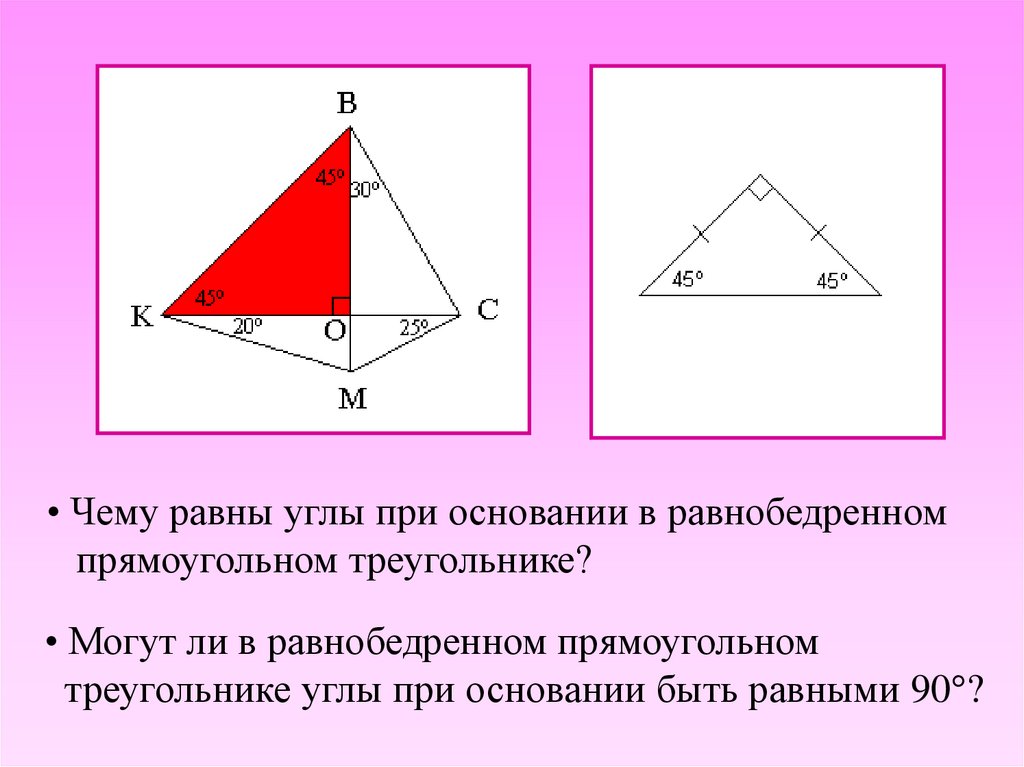
• Чему равны углы при основании в равнобедренномпрямоугольном треугольнике?
• Могут ли в равнобедренном прямоугольном
треугольнике углы при основании быть равными 90 ?
8.
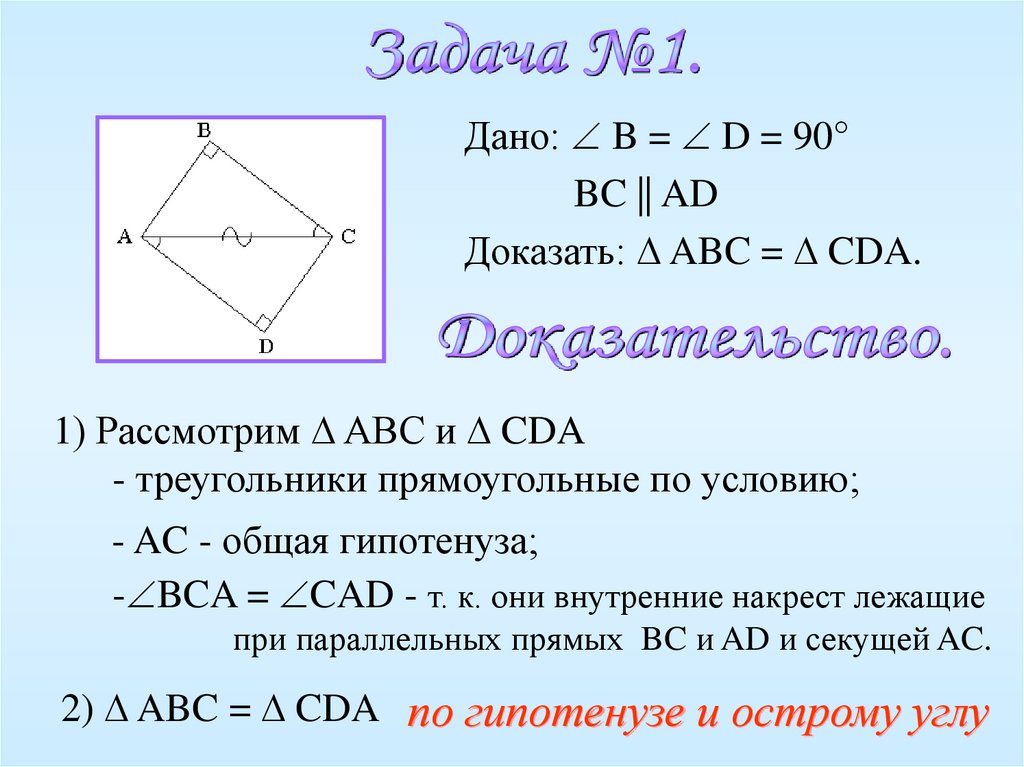
Дано: B = D = 90°BC || AD
Доказать: ABC = CDA.
1) Рассмотрим ABC и CDA
- треугольники прямоугольные по условию;
- AC - общая гипотенуза;
- BCA = CAD - т. к. они внутренние накрест лежащие
при параллельных прямых BC и AD и секущей AC.
2) ABC = CDA по гипотенузе и острому углу
9. Из точки D, лежащей на биссектрисе A, опущены перпендикуляры DB и DC на стороны угла. Докажите, что ADB = ADC.
Из точки D, лежащей на биссектрисе A, опущеныперпендикуляры DB и DC на стороны угла. Докажите,
что ADB = ADC.
Дано: AD - биссектриса A
DB AB, DC AC.
Доказать: ADB = ADC.
1) Рассмотрим ADB и ADC.
- треугольники прямоугольные т. к. DB AB, DC AC.
- AD - общая гипотенуза.
- BAD = CAD т. к. AD - биссектриса A.
2) ADB = ADC
по гипотенузе и острому углу.
10.
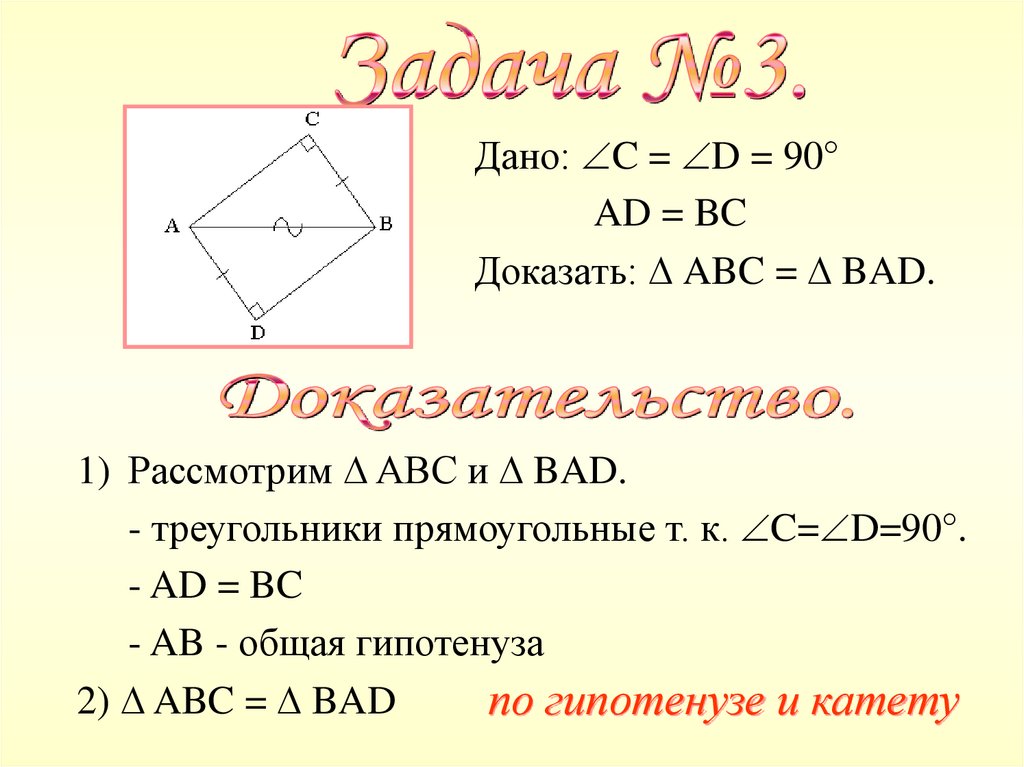
Дано: C = D = 90°AD = BC
Доказать: ABC = BAD.
1) Рассмотрим ABC и BAD.
- треугольники прямоугольные т. к. C= D=90°.
- AD = BC
- AB - общая гипотенуза
2) ABC = BAD
по гипотенузе и катету
11.
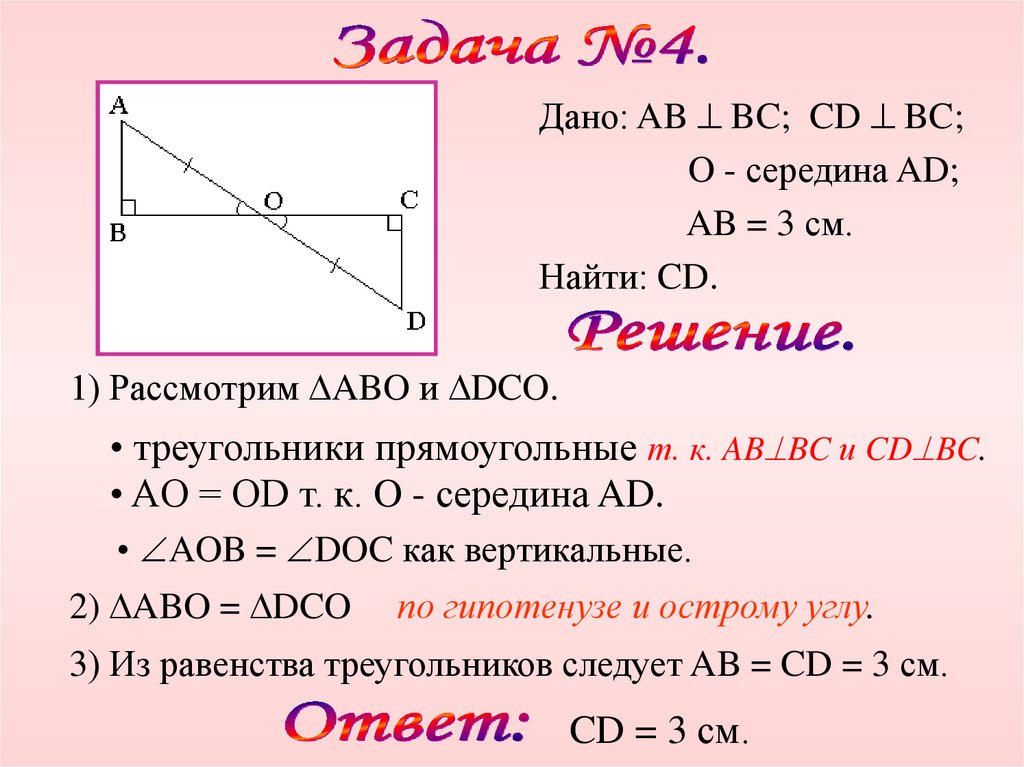
Дано: AB BC; CD BC;O - середина AD;
AB = 3 см.
Найти: CD.
1) Рассмотрим ABO и DCO.
• треугольники прямоугольные т. к. AB BC и CD BC.
• AO = OD т. к. O - середина AD.
• AOB = DOC как вертикальные.
2) ABO = DCO
по гипотенузе и острому углу.
3) Из равенства треугольников следует AB = CD = 3 см.
CD = 3 см.
12. Домашнее задание.
Устно: формулировки признаков.Письменно:
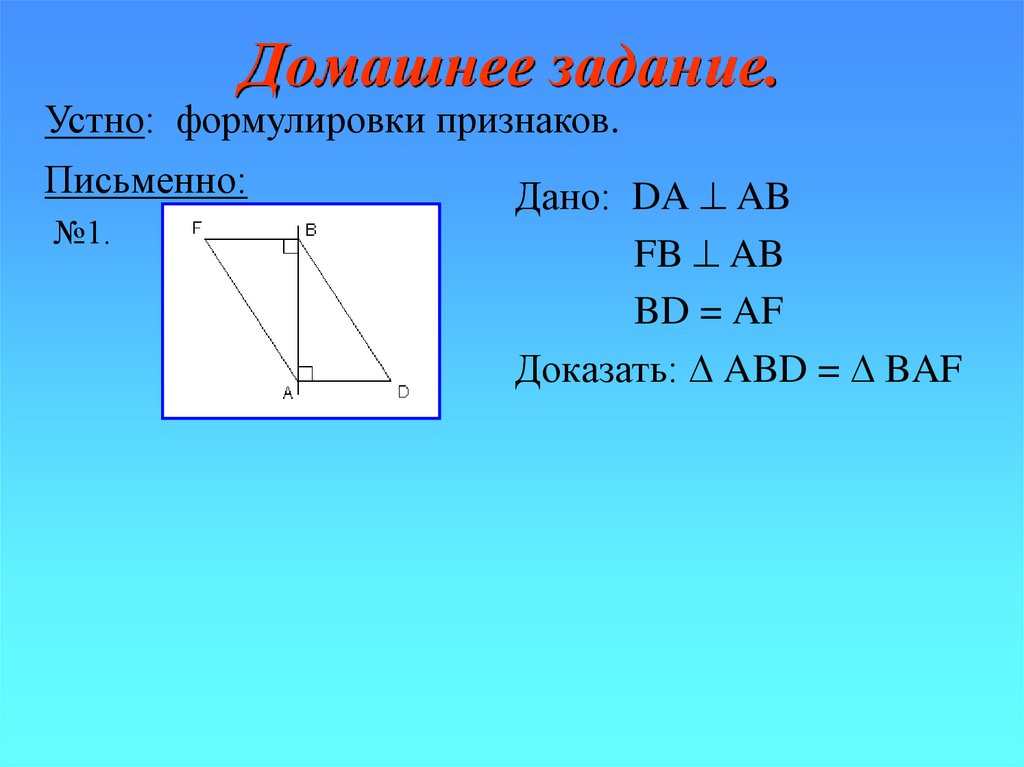
№1.
Дано: DA AB
FB AB
BD = AF
Доказать: ABD = BAF




 Математика
Математика








