Признаки равенства прямоугольных треугольников

1.

Признаки равенства
прямоугольных треугольников
Шиман О.А.

2.

В
Найти:
угол В
37 0
С
А

3.

В
Найти:
Угол САВ
70 0
А
Д
С

4.

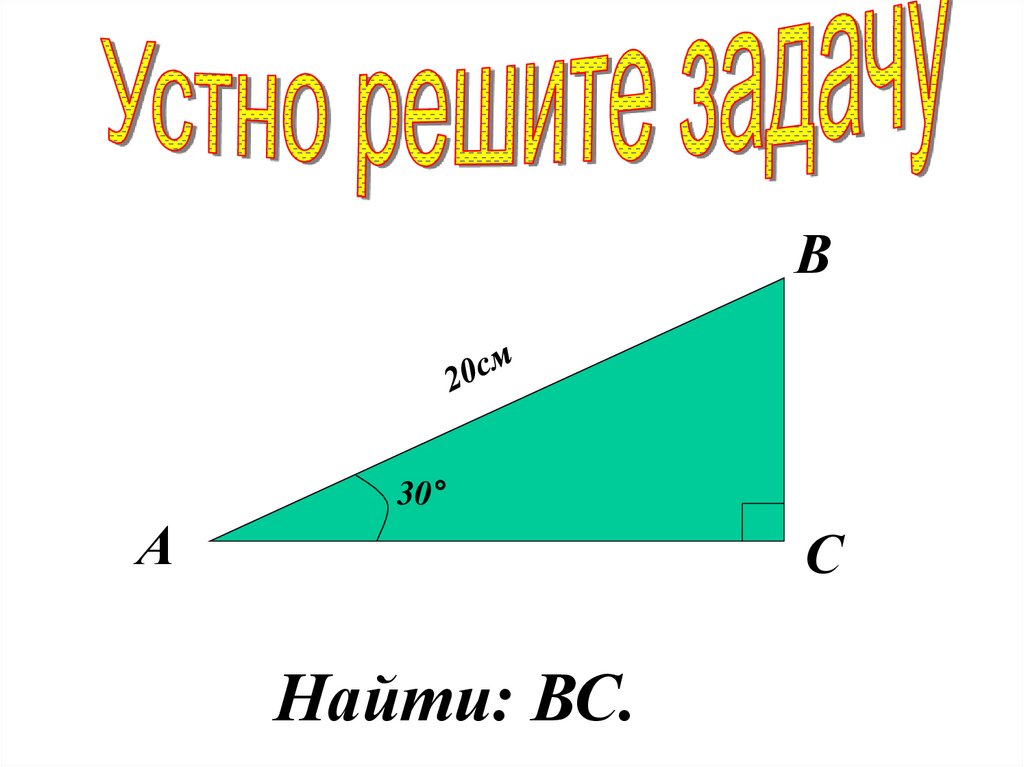
В
30°
А
С
Найти: ВС.

5.

Признаки
равенства
прямоугольных
треугольников

6.

Практическая работа по
группам
• 1 группа доказывает по двум катетам
• 2 группа доказывает по гипотенузе и
острому углу
• 3 группа доказывает по катету и
прилежащему острому углу
• 4 группа доказывает по гипотенузе и
катету

7.

по двум катетам
по гипотенузе и
катету
по катету и
противолежащему
острому углу
по гипотенузе и
острому углу
по катету и
прилежащему
острому углу

8.

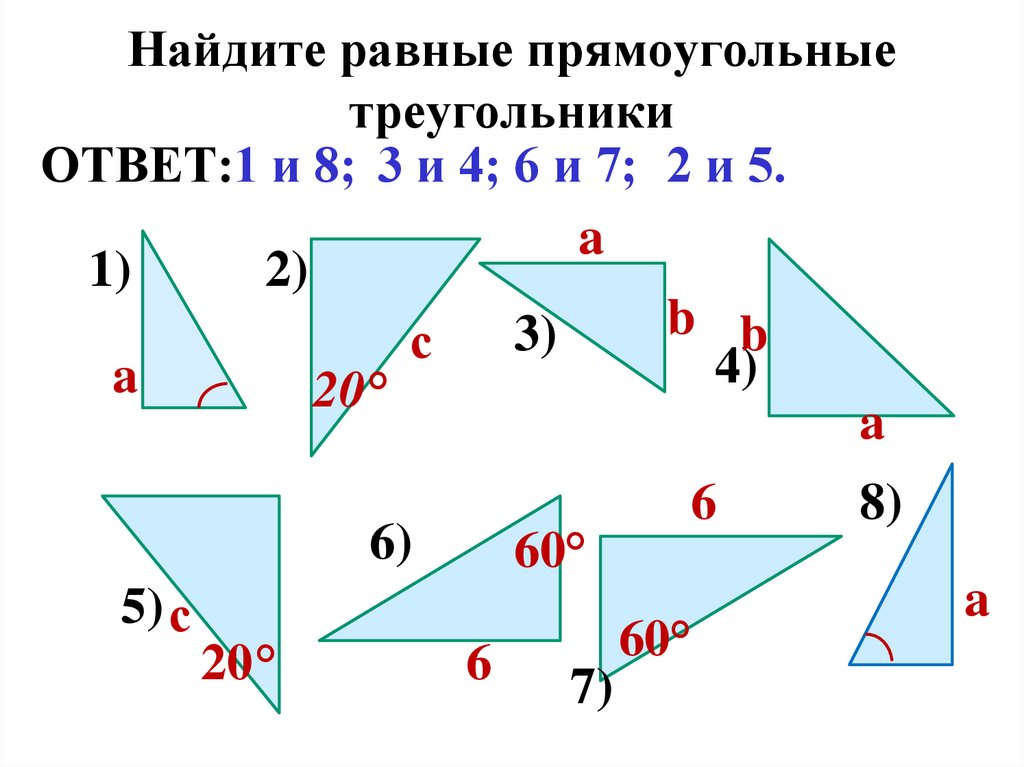
Найдите равные прямоугольные
треугольники
ОТВЕТ:1 и 8; 3 и 4; 6 и 7; 2 и 5.
a
1)
2)
b
3)
b
с
4)
a
20°
a
6
6)
60°
5) с
20°
8)
6
60°
7)
a

9.

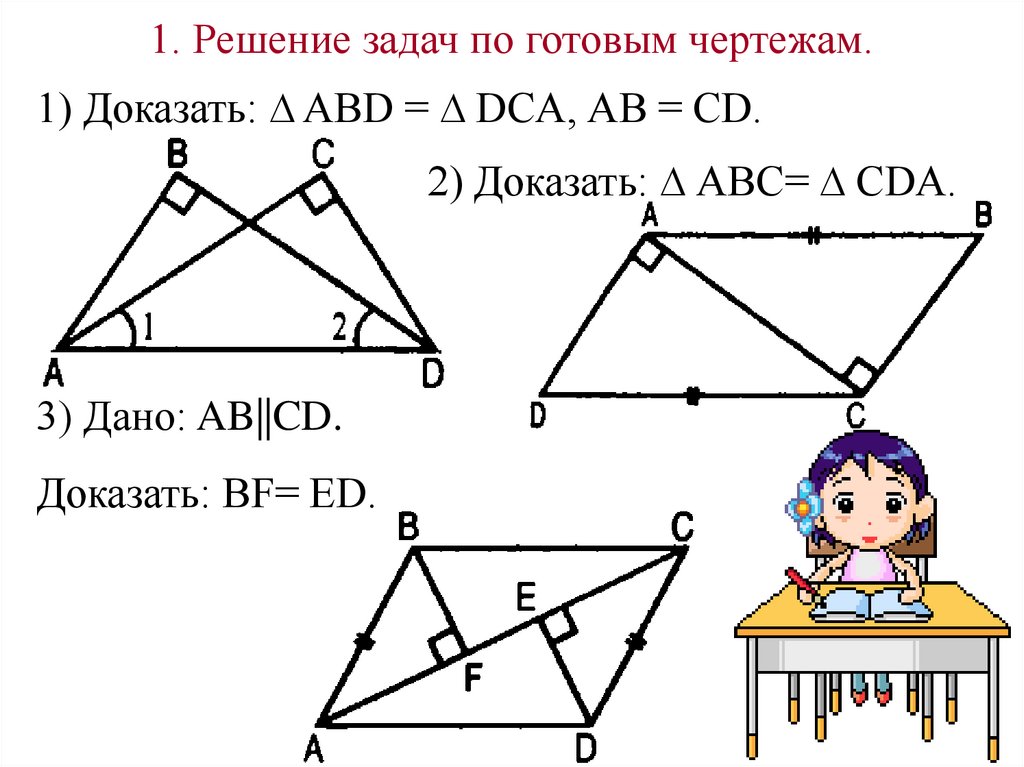
1. Решение задач по готовым чертежам.
1) Доказать: ∆ ABD = ∆ DCA, АВ = CD.
2) Доказать: ∆ АВС= ∆ CDA.
3) Дано: AB||CD.
Доказать: BF= ED.

10.

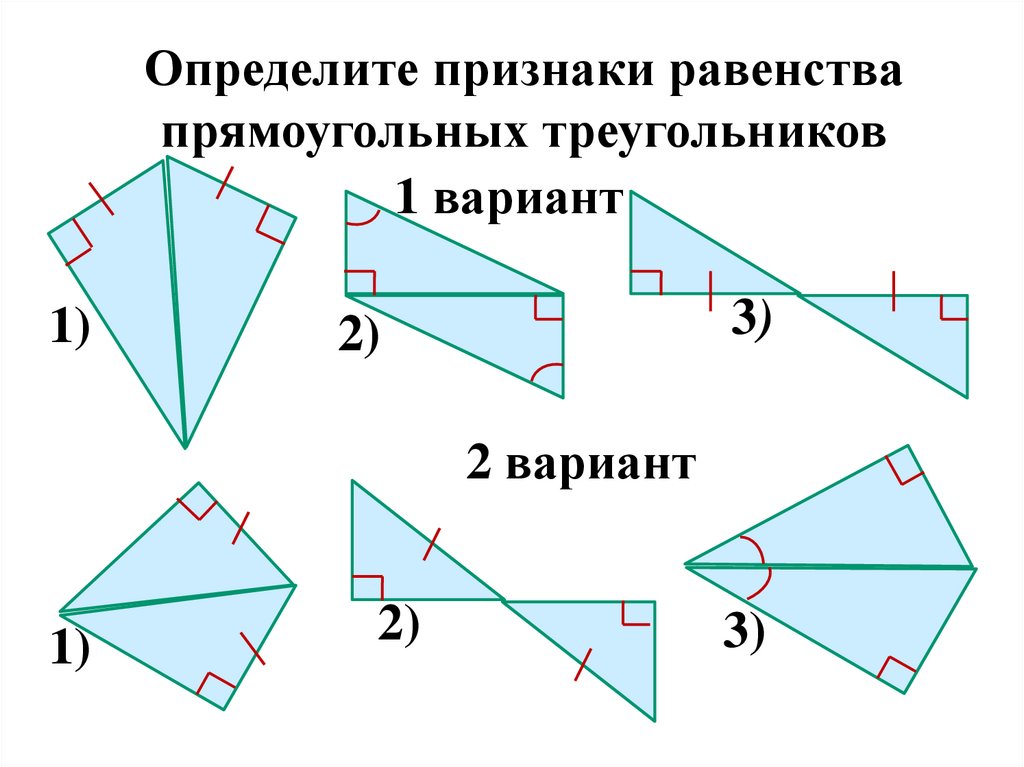
Определите признаки равенства
прямоугольных треугольников
1 вариант
1)
3)
2)
2 вариант
1)
2)
3)

11.

1) Найти: CAD.
CAD=150°.
3) Дано: АС= DC= 4.
Найти: BF.
BF=1.
2) Найти: AD.
AD = 15.
4) Найти: MD.
МD = 2.

12.

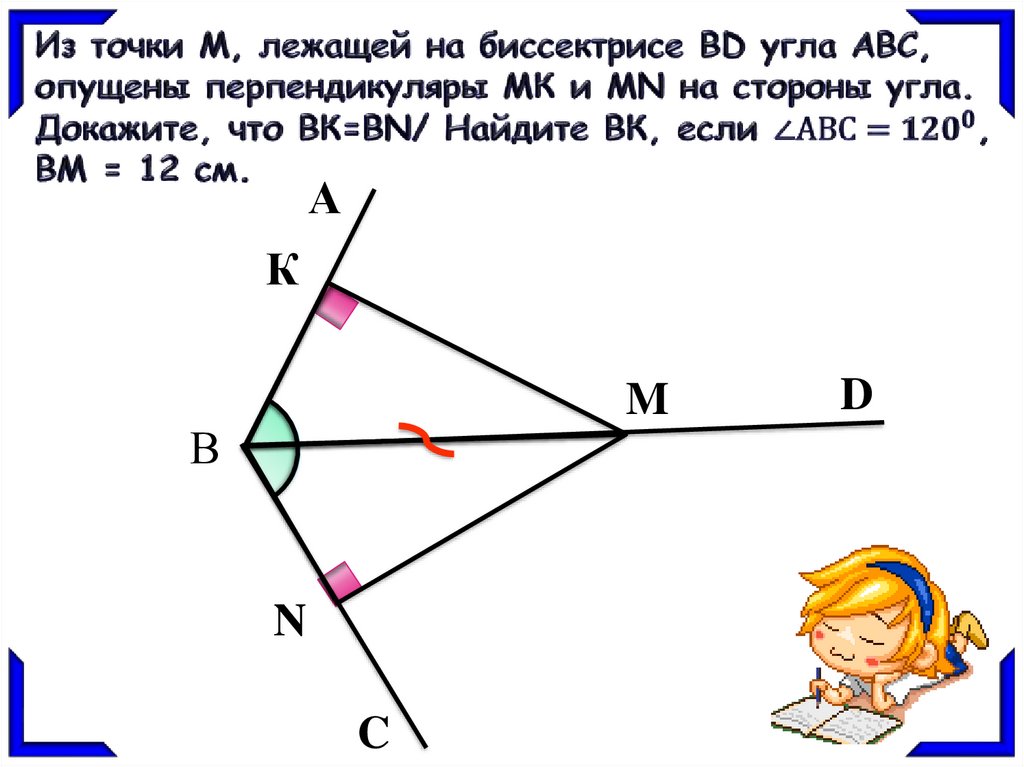
А
К
M
В
N
C
D

13.

Дано: B = D = 90°
BC || AD
Доказать: ABC = CDA.
по гипотенузе и острому углу

14.

Из точки D, лежащей на биссектрисе A, опущены
перпендикуляры DB и DC на стороны угла. Докажите,
что ADB = ADC.
Дано: AD - биссектриса A
DB AB, DC AC.
Доказать: ADB = ADC.
1) Рассмотрим ADB и ADC.
- треугольники прямоугольные т. к. DB AB, DC AC.
- AD - общая гипотенуза.
- BAD = CAD т. к. AD - биссектриса A.
2) ADB = ADC
по гипотенузе и острому углу.

15.

Дано: C = D = 90°
AD = BC
Доказать: ABC = BAD.
1) Рассмотрим ABC и BAD.
- треугольники прямоугольные т. к. C= D=90°.
- AD = BC
- AB - общая гипотенуза
2) ABC = BAD
по гипотенузе и катету

16.

Дано: AB BC; CD BC;
O - середина AD;
AB = 3 см.
Найти: CD.
1) Рассмотрим ABO и DCO.
• треугольники прямоугольные т. к. AB BC и CD BC.
• AO = OD т. к. O - середина AD.
• AOB = DOC как вертикальные.
2) ABO = DCO
по гипотенузе и острому углу.
3) Из равенства треугольников следует AB = CD = 3 см.
CD = 3 см.