Примеры адаптивных систем

1.

Профессор, д.т.н.
Ермолаев Виктор Тимофеевич
Лекция 1
1

2. Примеры адаптивных систем

С помощью адаптивных систем решаются
следующие задачи:
1. Прием и обработка сигналов, в том числе
обнаружение, фильтрация, измерение параметров и
разрешение сигналов, подавление мешающих сигналов;
2. Автоматическое управление динамическими
объектами;
3. Распознавание образов;
4. Идентификация неизвестных систем;
5. Выравнивание частотных характеристик связных
радиоканалов;
6. Коррекция оптических изображений;
7. Гашение волновых полей.
2

3. Линейный фильтр (1)

y(t)
K(j )
y(t)=uc(t)+un(t);
K ( j )
2
S c ( j )
2
min<| (t)- uc(t)|2>
Sc ( j ) S n ( j )
2
(t)
2
Решение Винера
для оптимального
фильтра
Sc(j ) – спектр полезного сигнала, Sn(j ) – спектр помехи
Оптимальный фильтр можно построить, если спектр помехи известен!
Когда нет априорной информации о спектре помехи, можно построить
адаптивный фильтр, близкий по своим характеристикам к оптимальному
фильтру. Для этого система должна оценить спектр помехи по входному
сигналу помехи и использовать эту оценку для определения коэффициента
передачи фильтра K(j ).
3

4. Линейный фильтр (2)

y(t)
K(j )
(t)
uc (t0 )
y(t)=uc(t)+un(t);
max
2
0,5
(
u
)
n
Sc ( j )
K ( j ) a
exp( j t0 )
2
S n ( j )
Критерий
максимального
ОСШ
Sc(j ) – спектр полезного сигнала, Sn(j ) – спектр помехи
Когда сигнал наблюдается на фоне собственного шума, Sn(j )=const и K(j )
зависит только от спектра полезного сигнала Sс(j ). В этом случае может быть
реализован оптимальный фильтр. Он называется также согласованным
фильтром, поскольку K(j ) S*с(j ), где звездочка вверху обозначает
комплексное сопряжение. Когда помеха имеет неизвестный и неравномерный в
полосе сигнала спектр, требуется адаптивный подход для реализации фильтра.
4

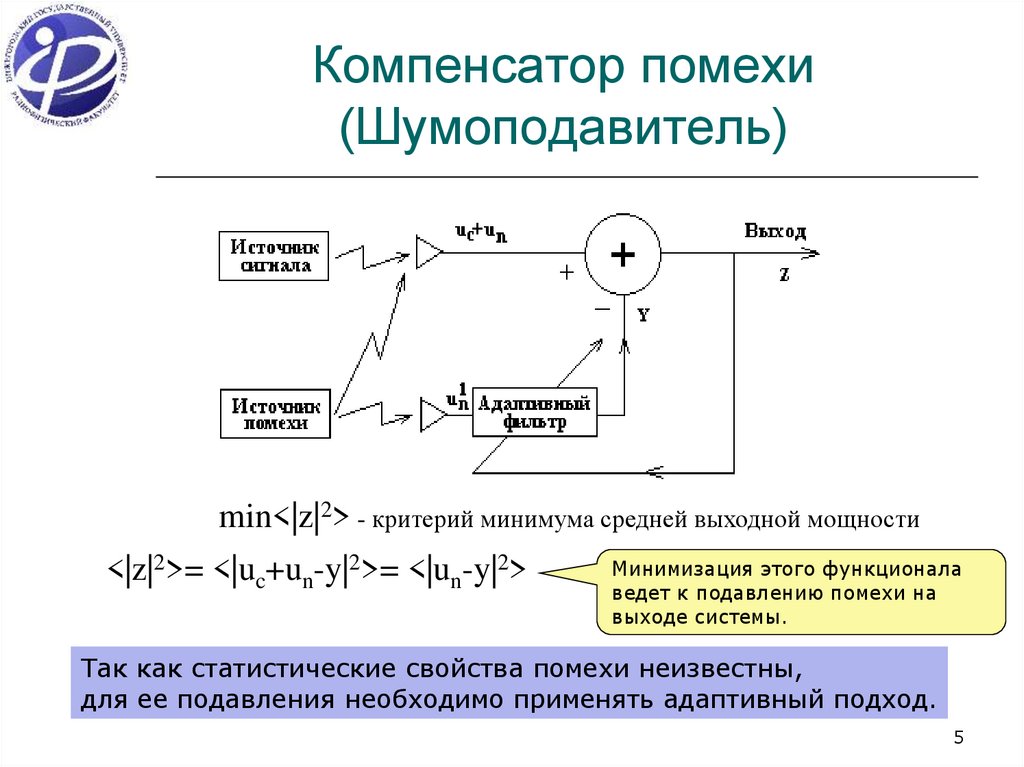
5. Компенсатор помехи (Шумоподавитель)

min<|z|2> - критерий минимума средней выходной мощности
<|z|2>= <|uc+un-y|2>= <|un-y|2>
Минимизация этого функционала
ведет к подавлению помехи на
выходе системы.
Так как статистические свойства помехи неизвестны,
для ее подавления необходимо применять адаптивный подход.
5

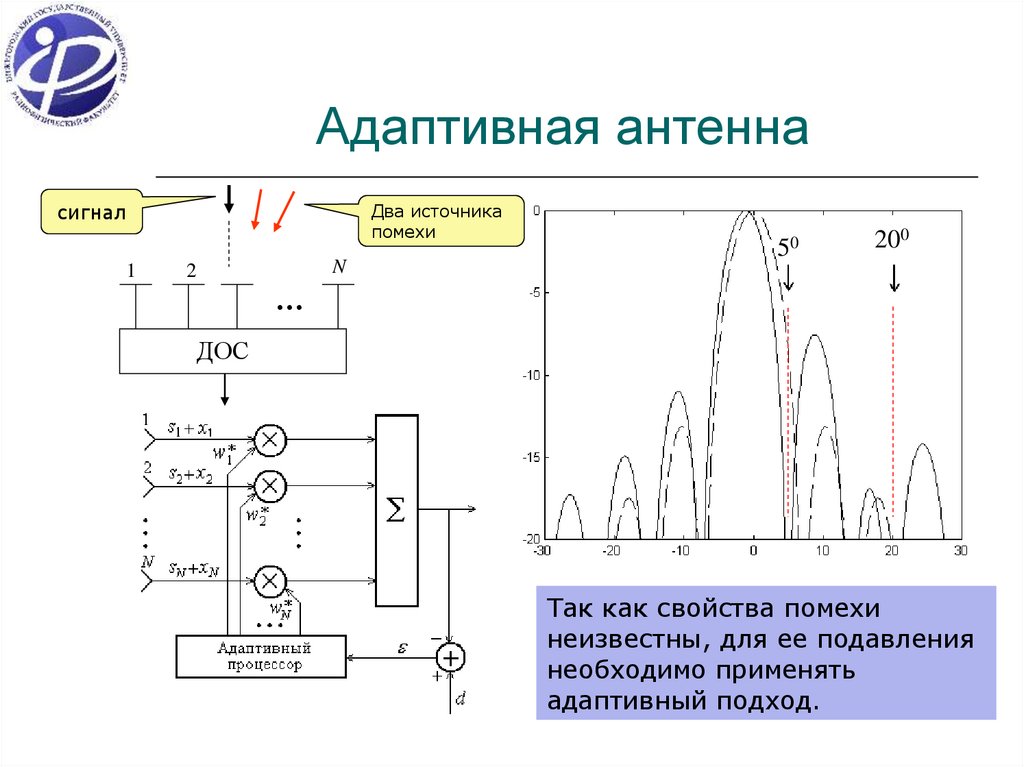
6. Адаптивная антенна

сигнал
1
Два источника
помехи
N
2
50
200
…
ДОС
Так как свойства помехи
неизвестны, для ее подавления
необходимо применять
адаптивный подход.

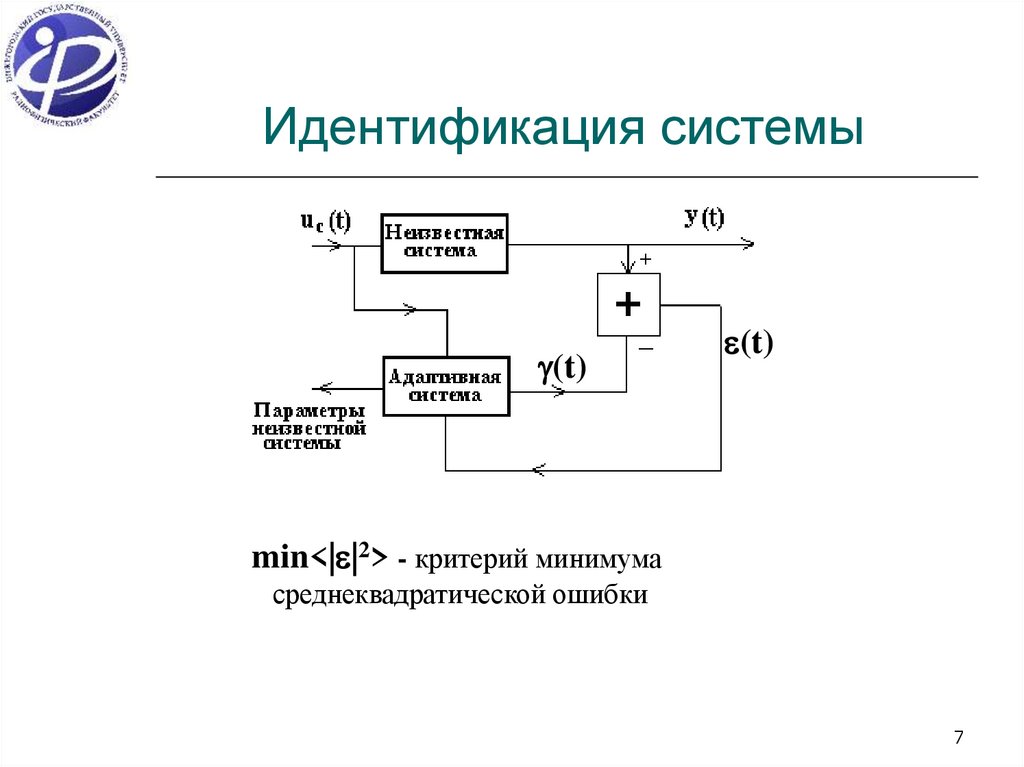
7. Идентификация системы

(t)
(t)
min<| |2> - критерий минимума
среднеквадратической ошибки
7

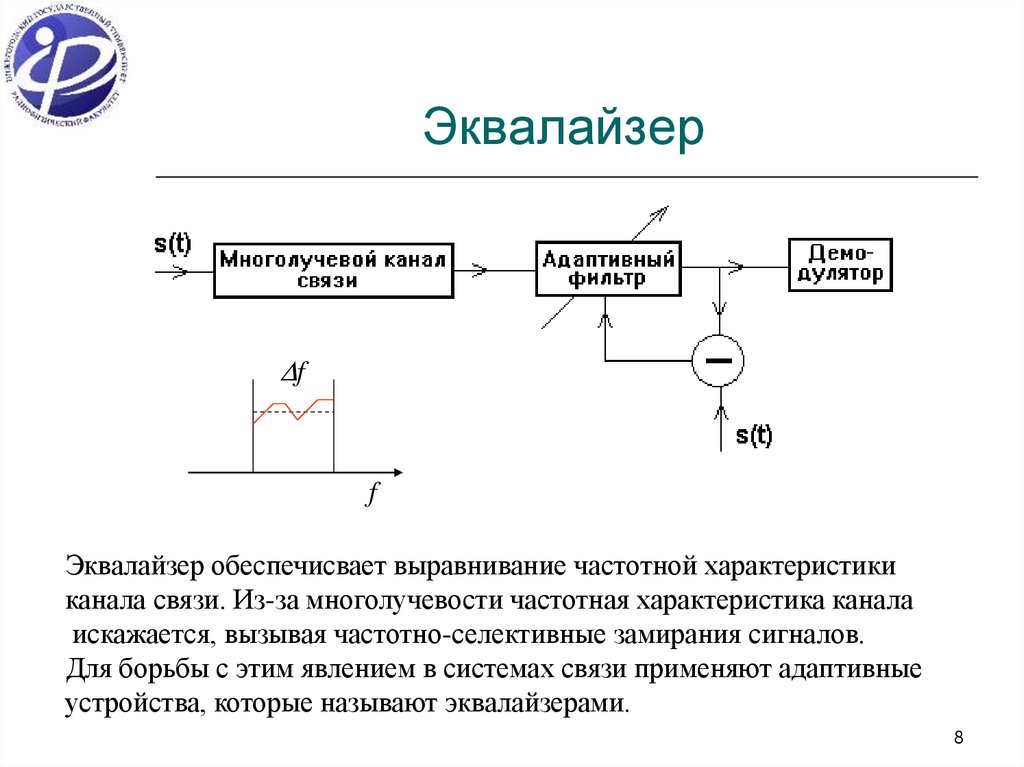
8. Эквалайзер

f
f
Эквалайзер обеспечисвает выравнивание частотной характеристики
канала связи. Из-за многолучевости частотная характеристика канала
искажается, вызывая частотно-селективные замирания сигналов.
Для борьбы с этим явлением в системах связи применяют адаптивные
устройства, которые называют эквалайзерами.
8

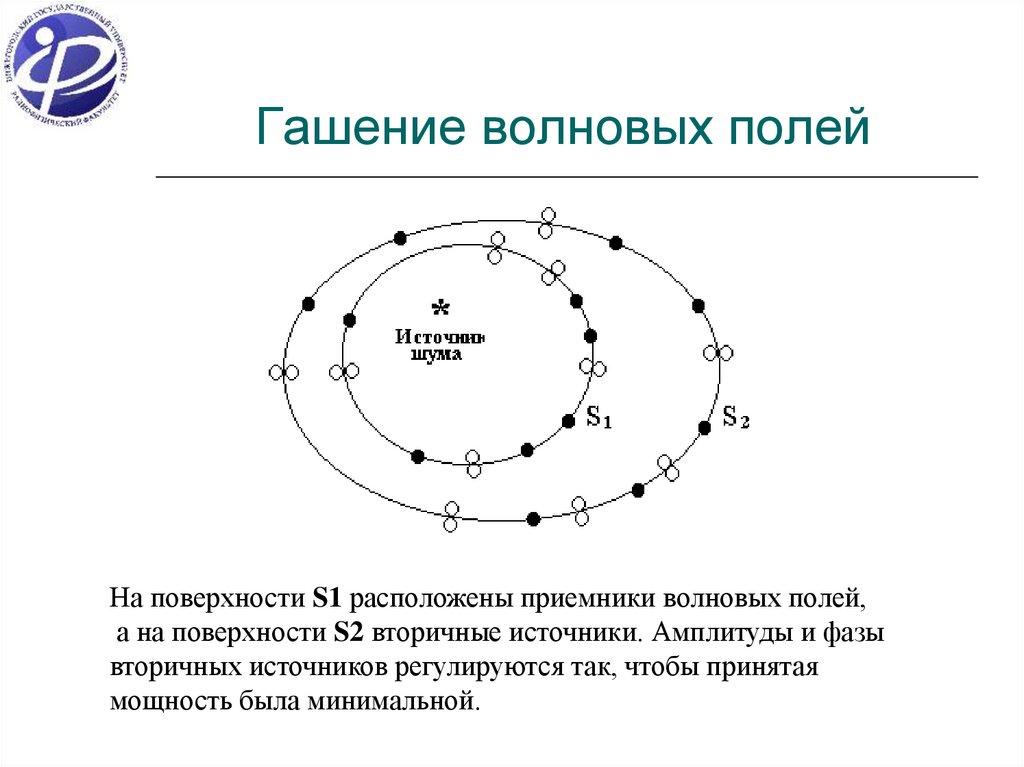
9. Гашение волновых полей

На поверхности S1 расположены приемники волновых полей,
а на поверхности S2 вторичные источники. Амплитуды и фазы
вторичных источников регулируются так, чтобы принятая
мощность была минимальной.

10. Примеры адаптивных систем

Из рассмотренных примеров мы можем
сделать следующие выводы:
•Необходимость применения адаптивных систем
возникает тогда, когда синтез оптимальных систем
или невозможен, или когда потери в эффективности
из-за имеющейся априорной неопределенности
недопустимо велики;
•Адаптивные системы изменяют свои параметры в
процессе работы в соответствии с изменениями
сигнально-помеховой обстановки;
•Для настройки параметров адаптивной системы
требуется определенное время, которое называется
временем адаптации системы.
10

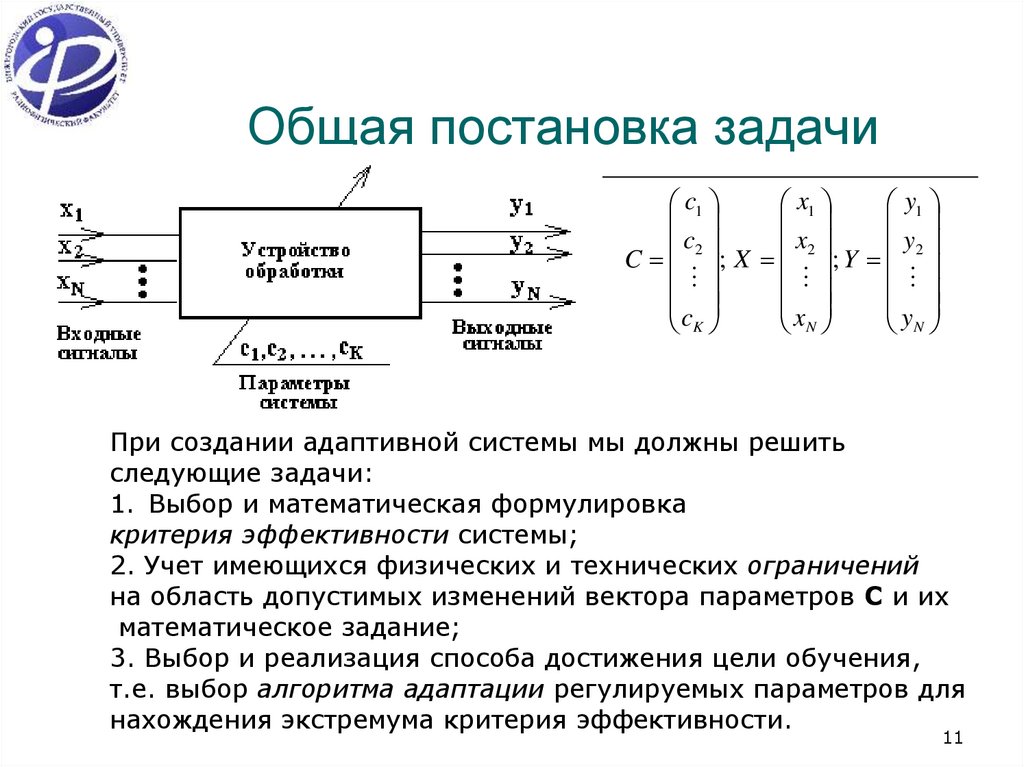
11. Общая постановка задачи

x1
y1
c1
x
c
2
y2
2
C ; X ; Y
c
x
y
K
N
N
При создании адаптивной системы мы должны решить
следующие задачи:
1. Выбор и математическая формулировка
критерия эффективности системы;
2. Учет имеющихся физических и технических ограничений
на область допустимых изменений вектора параметров C и их
математическое задание;
3. Выбор и реализация способа достижения цели обучения,
т.е. выбор алгоритма адаптации регулируемых параметров для
нахождения экстремума критерия эффективности.
11

12. Критерий эффективности (1)

• Минимум среднеквадратической ошибки
(СКО);
• Минимум выходной мощности помехи;
• Максимум выходного отношения мощностей
полезного сигнала и помехи;
• Минимум вероятности ошибочных решений;
• Минимум уровня мощности остаточного поля в
контрольных точках (система гашения волн);
• Точность оценивания параметров неизвестной
системы.
12

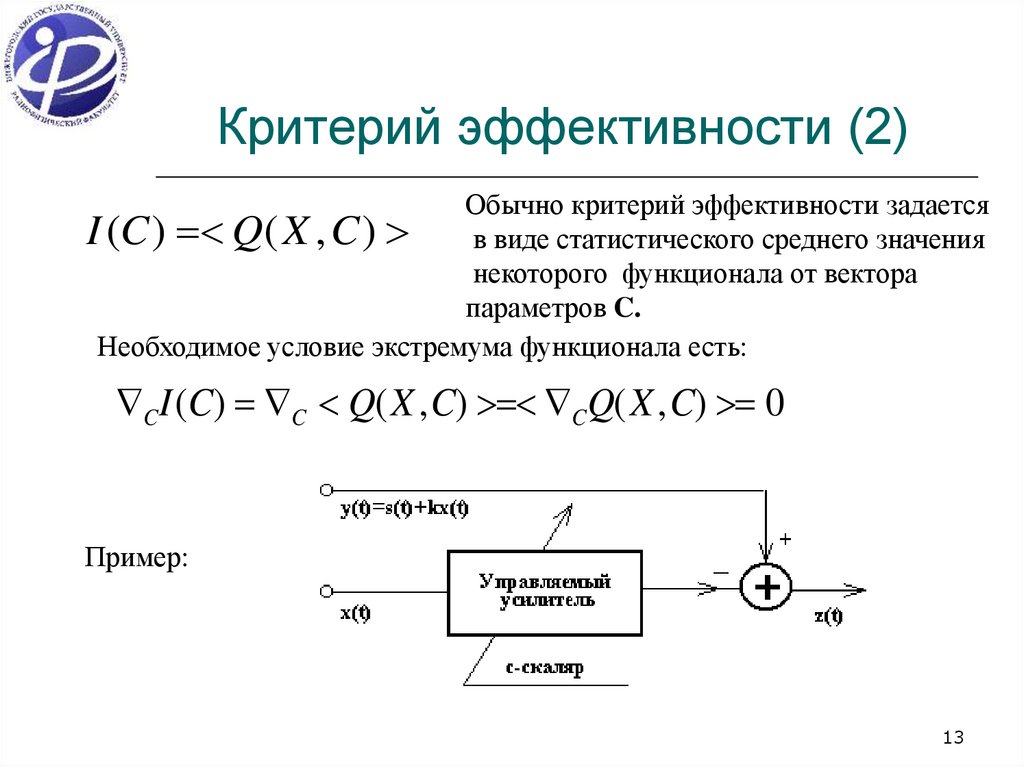
13. Критерий эффективности (2)

Обычно критерий эффективности задается
I (C ) Q( X , C ) в виде статистического среднего значения
некоторого функционала от вектора
параметров C.
Необходимое условие экстремума функционала есть:
CI (C) C Q( X , C) CQ( X , C) 0
Пример:
13

14. Критерий эффективности (3)

Q( X , C ) z (t ) y(t ) cx(t )
2
2
y 2 (t ) 2cy(t ) x(t ) c 2 x 2 (t )
I (C) z 2 (t ) y 2 (t ) 2c y(t ) x(t ) c2 x 2 (t )
14

15. Критерий эффективности (4)

dI (c)
2 y(t ) x(t ) 2c x 2 (t ) 0
dc
dI (c)
2 z(t ) x(t ) 0
dc
y (t ) x (t ) k x 2 (t )
copt
k
2
2
x (t )
x (t )
15

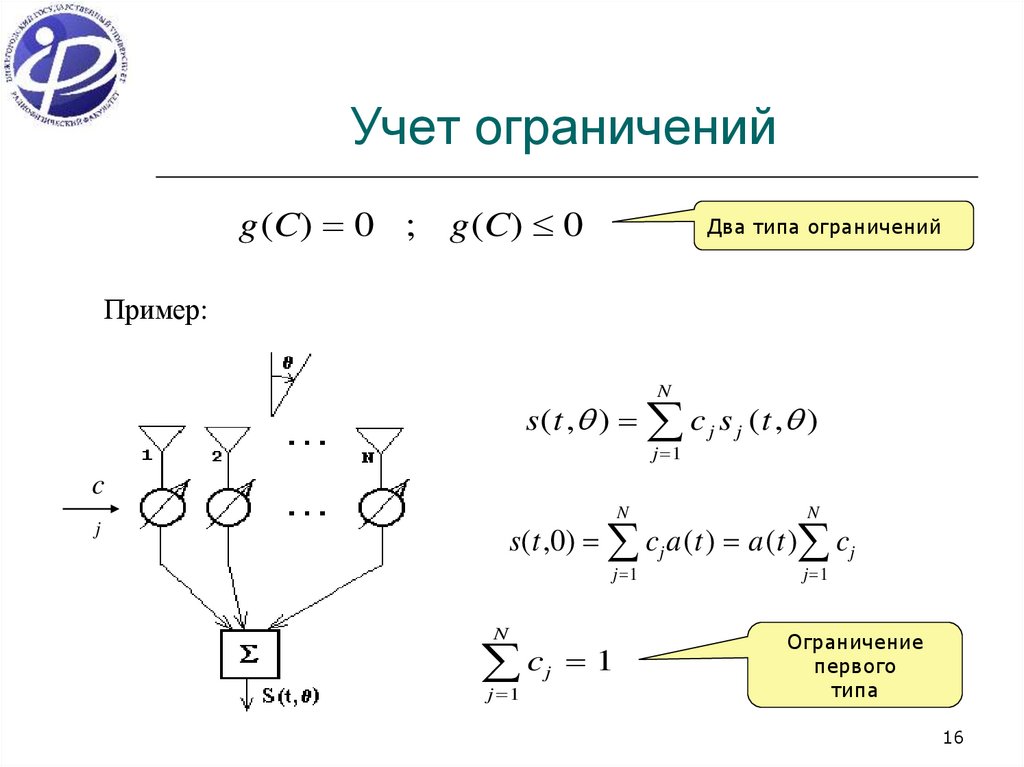
16. Учет ограничений

g (C) 0 ; g (C) 0
Два типа ограничений
Пример:
N
s( t , ) c j s j ( t , )
j 1
c
N
N
j 1
j 1
s( t ,0) cj a ( t ) a ( t ) cj
j
N
c 1
j
j 1
Ограничение
первого
типа
16

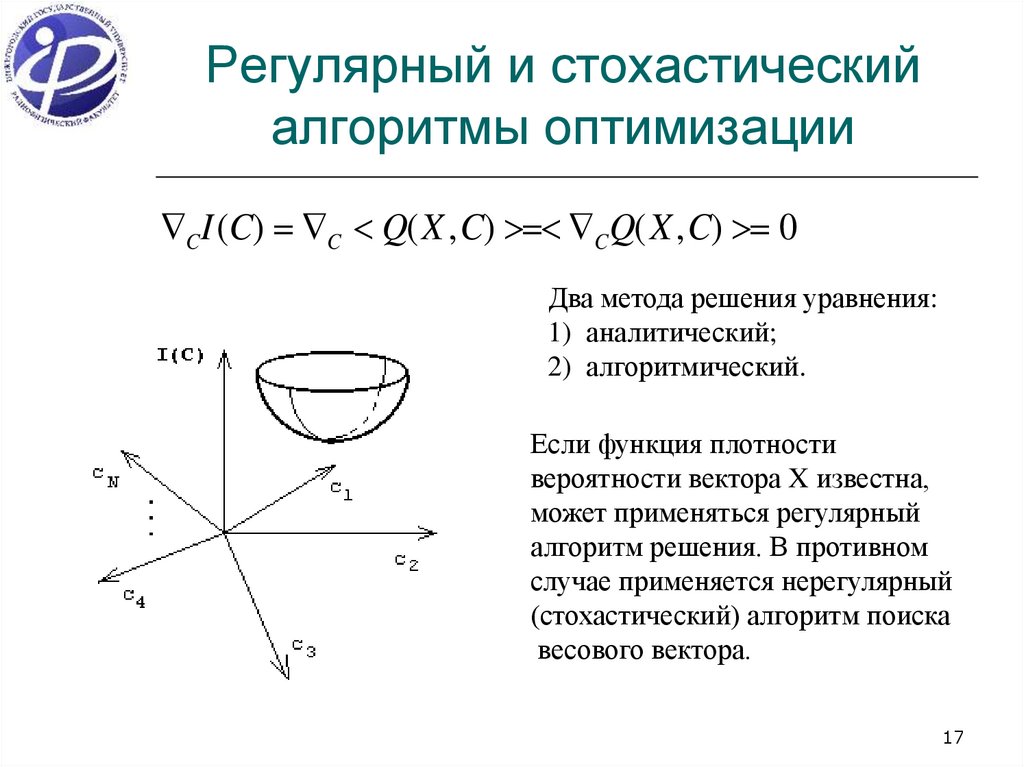
17. Регулярный и стохастический алгоритмы оптимизации

CI (C) C Q( X , C) CQ( X , C) 0
Два метода решения уравнения:
1) аналитический;
2) алгоритмический.
Если функция плотности
вероятности вектора X известна,
может применяться регулярный
алгоритм решения. В противном
случае применяется нерегулярный
(стохастический) алгоритм поиска
весового вектора.
17

18.

18