Похожие презентации:
Поверхности второго порядка. Тема 13
1.
§13. Поверхности второгопорядка
п.1. Цилиндрические поверхности.
Цилиндрической поверхностью называется
поверхность, составленная из всех прямых,
пересекающих данную линию L и
параллельных данной прямой l.
Линия L называется направляющей
цилиндрической поверхности.
Каждая из параллельных прямых,
составляющих поверхноссть называется
образующей.
2.
Рассмотрим цилиндрические поверхности снаправляющими, лежащими в одной из
координатных плоскостей, и образующими,
перпендикулярными этой плоскости.
Уравнение цилиндра с образующими,
параллельными оси Oz, имеет следующий вид
F ( x , y ) 0.
В этом уравнении отсутствует координата z.
Аналогичные утверждения справедливы и для
других случаев размещения образующих.
3.
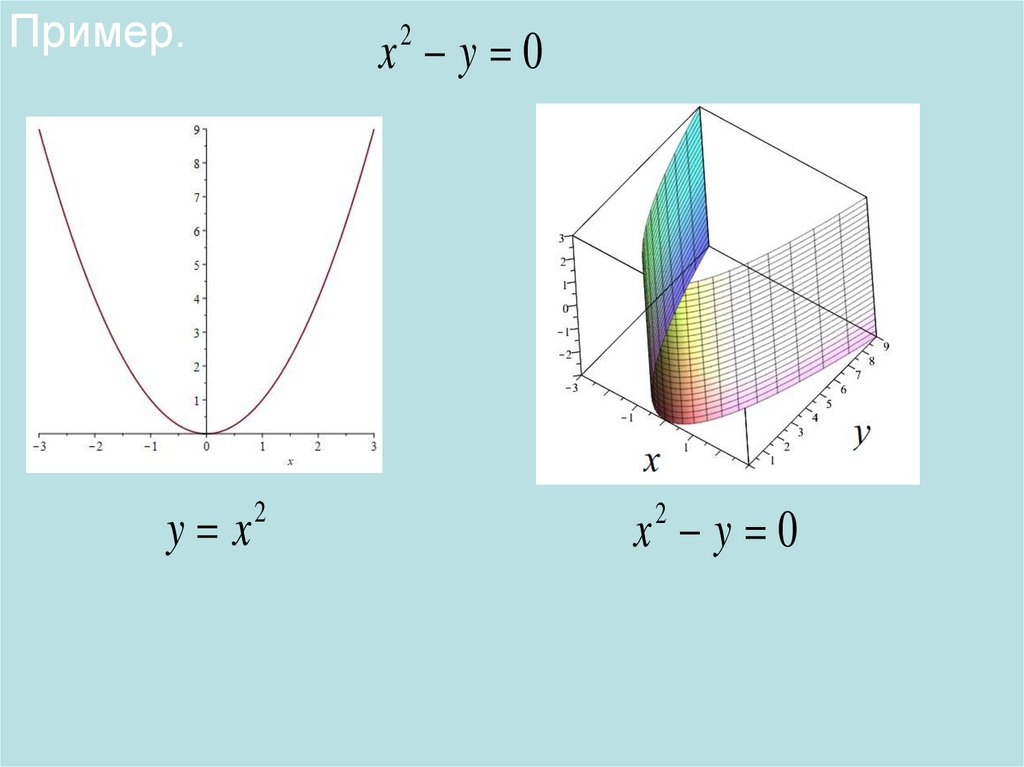
Пример.y x
x y 0
2
2
x y 0
2
4.
п.2. Поверхности вращения.Поверхность вращения - это поверхность,
образованная вращением двумерной кривой
вокруг оси.
Если ось вращения совпадает с осью Oz, то
уравнение поверхности вращения выглядит
следующим образом:
F ( x y , z ) 0.
2
2
5.
Если ось вращения совпадает с осью Oy, тоуравнение поверхности вращения выглядит
следующим образом:
F ( x z , y ) 0.
2
2
Если ось вращения совпадает с осью Ox, то
уравнение поверхности вращения выглядит
следующим образом:
F ( y z , x ) 0.
2
2
6.
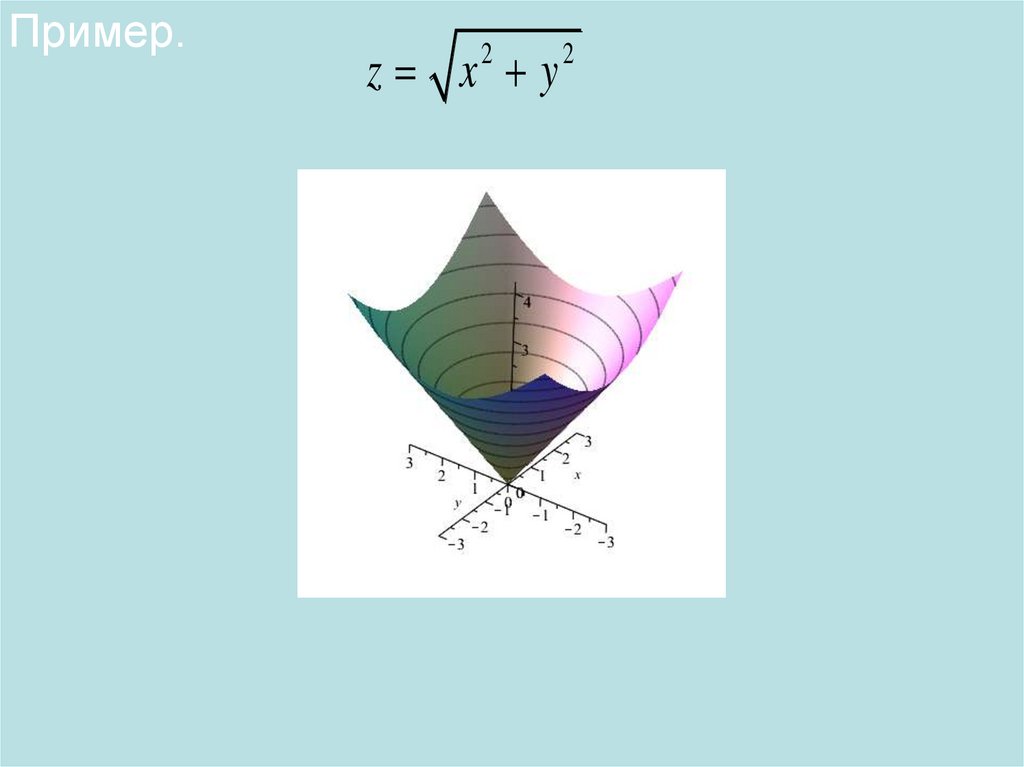
Пример.z x y
2
2
7.
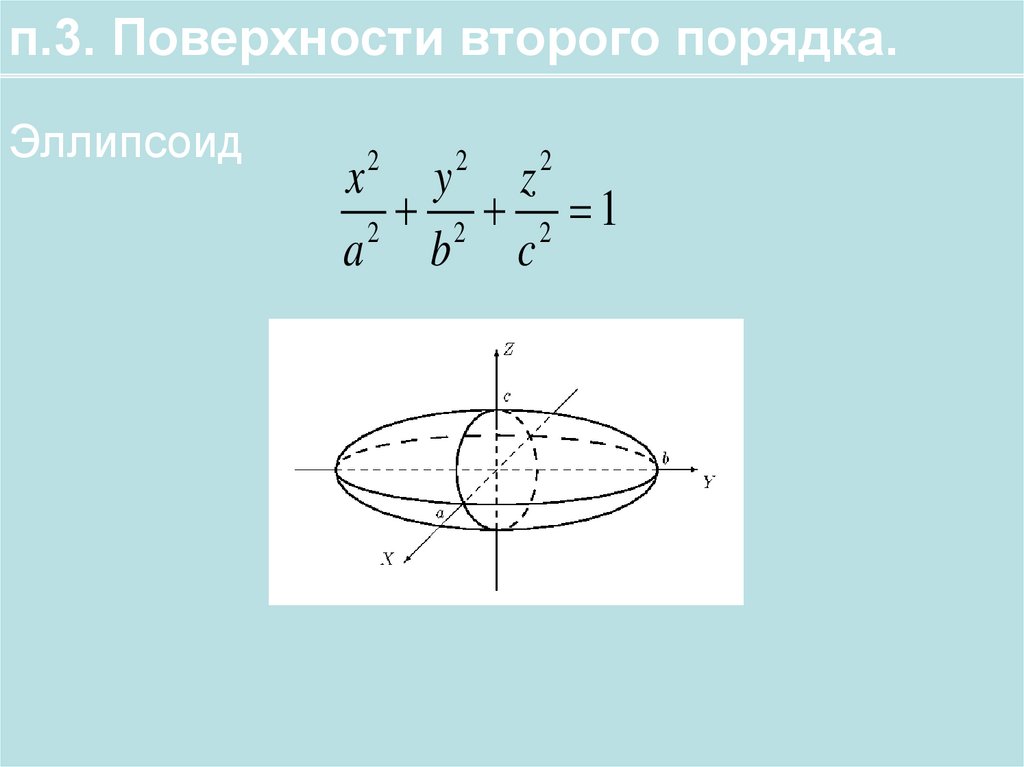
п.3. Поверхности второго порядка.Эллипсоид
2
2
2
x y z
2 2 1
2
a b c
8.
Однополостный гиперболоид2
2
2
x y z
2 2 1
2
a b c
9.
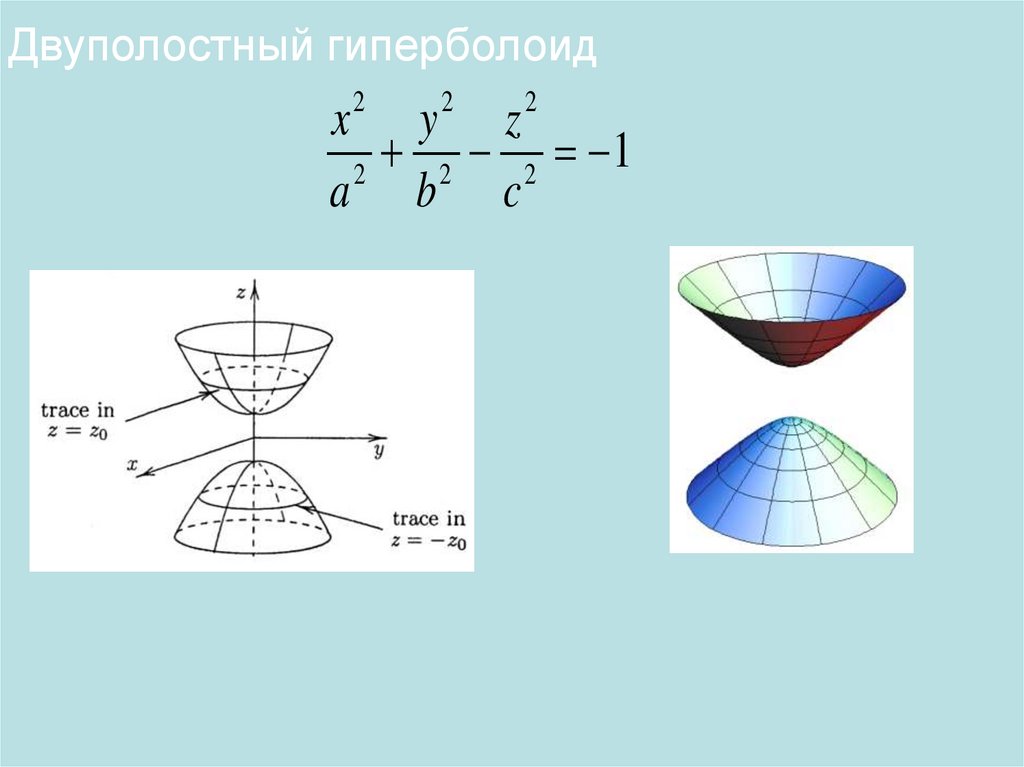
Двуполостный гиперболоид2
2
2
x y z
2 2 1
2
a b c
10.
Эллиптический параболоид2
2
x y
2z
p q
11.
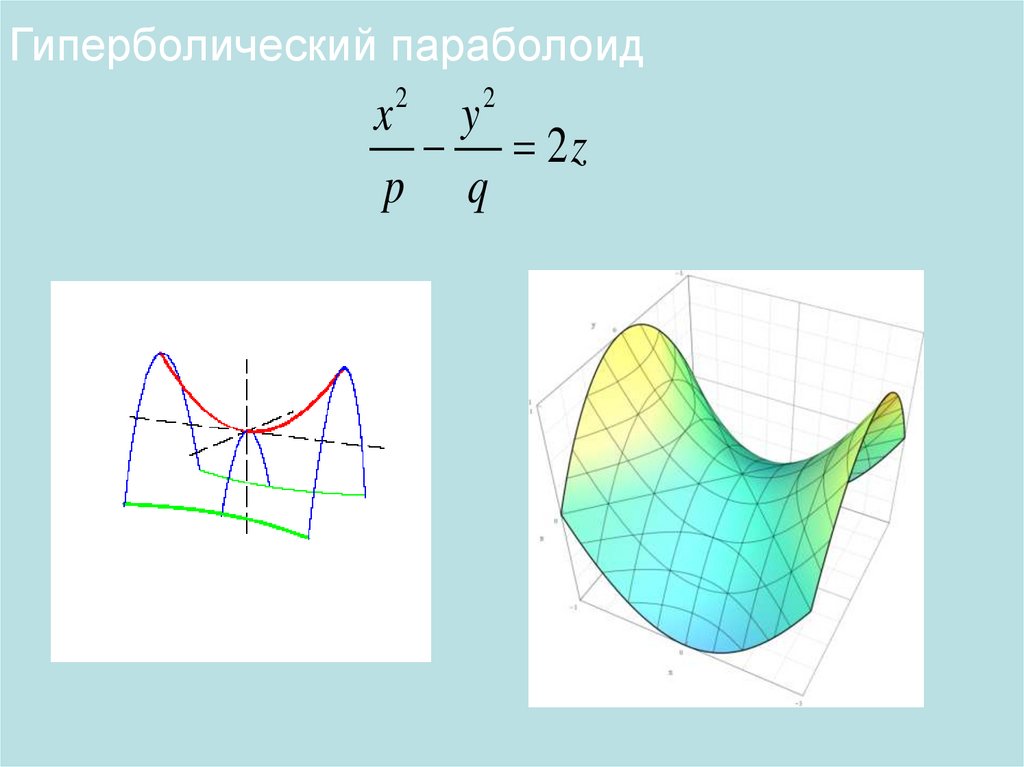
Гиперболический параболоид2
2
x y
2z
p q






 Математика
Математика








