Похожие презентации:
Формула Ньютона-Лейбница
1.
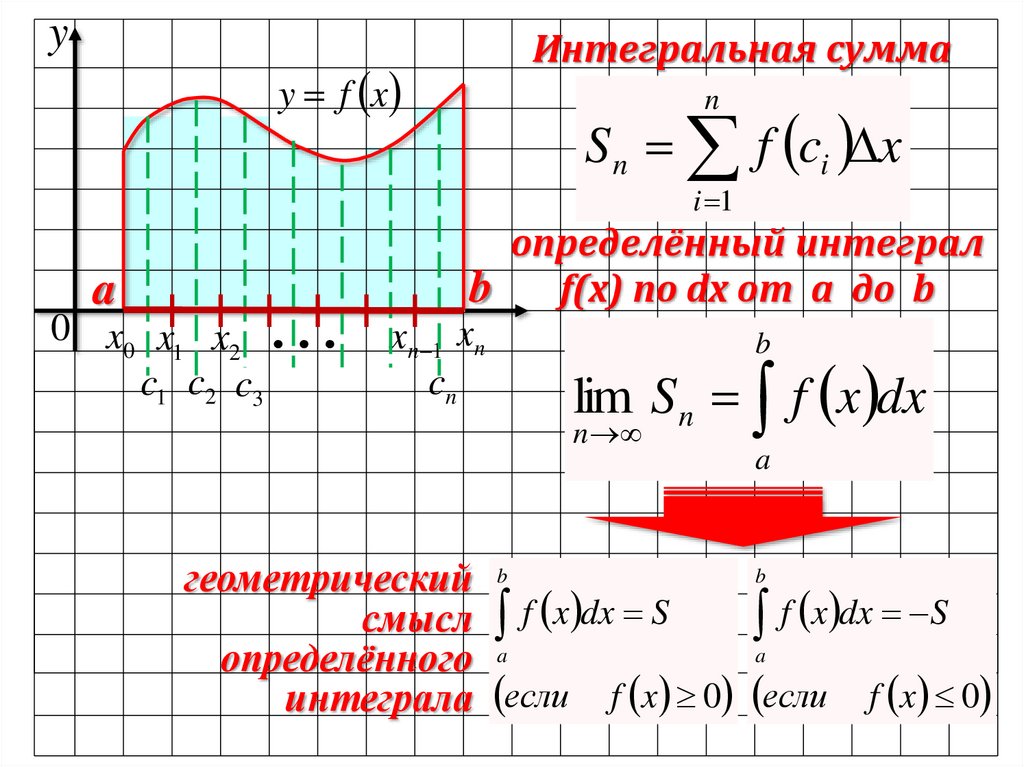
yy f x
Интегральная сумма
n
S n f ci x
i 1
a
0 x0 x x
1
2
c1 c2 c3
определённый интеграл
b f(x) по dx от a до b
xn 1 xn
b
cn
lim S f x dx
n
n
a
b
геометрический b
f x dx S
смысл f x dx S
a
определённого a
интеграла если f x 0 если f x 0
2.
fv lim
f ' x f f ' x x x
x 0 x
главная линейная часть приращения
функции- дифференциал функции
'
# df x f x x
f ( x) x dx x x dx x
'
df x f x dx
'
#
df
f x
dx
'
б.м.
3.
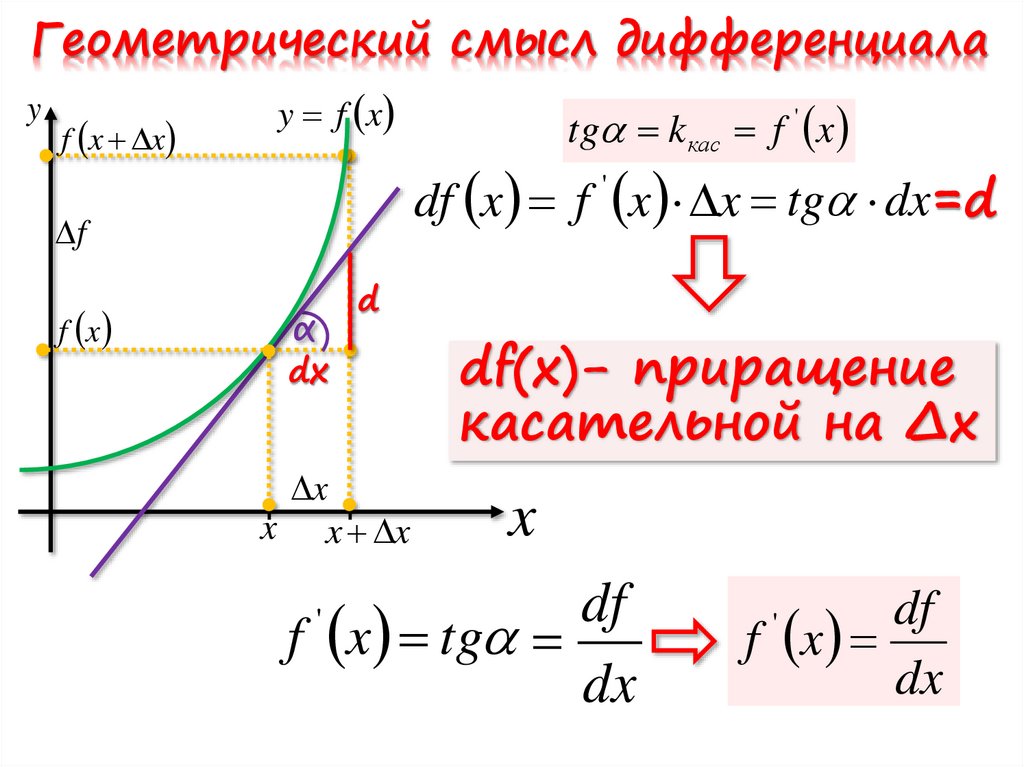
Геометрический смысл дифференциалаy
f x x
y f x
tg k кас f ' x
df x f x x tg dx=d
'
f
f x
α
dx
d
x
x x x
df(x)- приращение
касательной на ∆x
x
df
f x tg
dx
'
df
f x
dx
'
4.
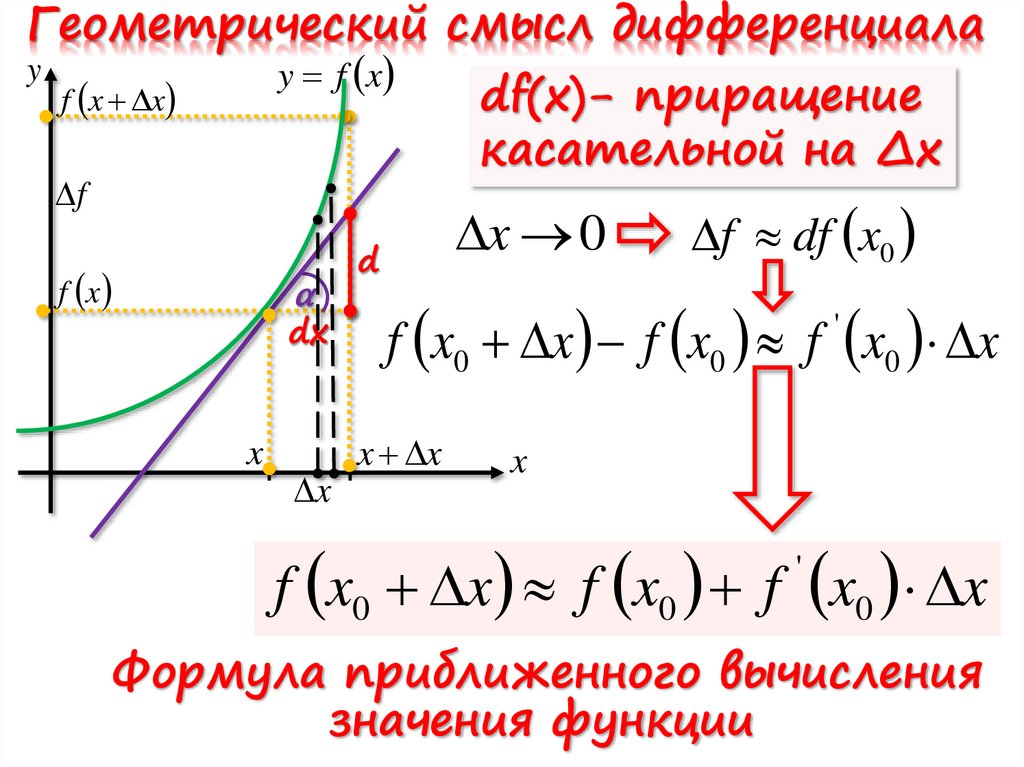
Геометрический смысл дифференциалаy
y f x
f x x
df(x)- приращение
касательной на ∆x
f
f x
α
dx
x
x
x 0
d
f df x0
f x0 x f x0 f x0 x
'
x x
x
f x0 x f x0 f x0 x
'
Формула приближенного вычисления
значения функции
5.
п f x0 x f x0 f x0 xр
1
1
0,02 1,01
1
,
02
1
0
,
02
и
2 1
м f x x
е '
1
f
x
р
2 x
'
6.
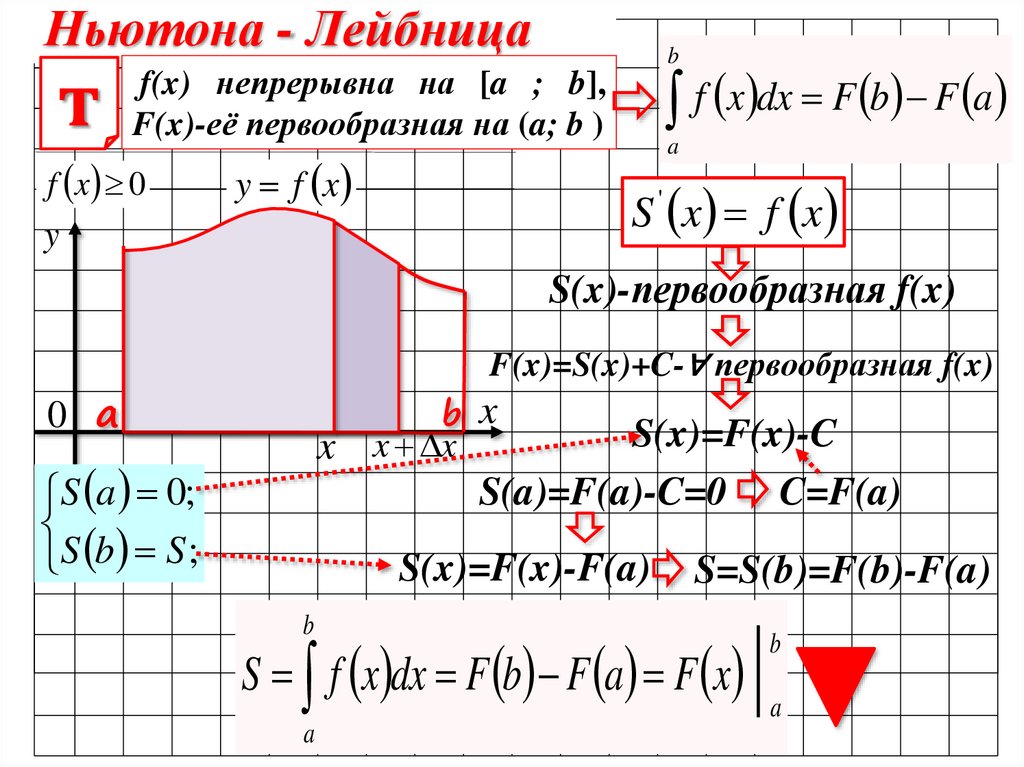
Ньютона - Лейбницат
f(x) непрерывна на [a ; b],
F(x)-её первообразная на (a; b )
f x 0
y f x
y
b
f x dx F b F a
a
S a 0
S x f x dx;
S b S
a
x
f x x f x f ' x x
0 a
x x x
b x
x 0
2 f x f ' x x
f ' x x
f x x f x
S x f x dx S тр .
x
x f x
x
2
2
2
x 0
x
x x
'
f
x
S
'
lim f x
x f x
S x lim
x 0
x 0 x
2
S x f x
'
7.
Ньютона - Лейбницат
b
f x dx F b F a
f(x) непрерывна на [a ; b],
F(x)-её первообразная на (a; b )
f x 0
y f x
a
S ' x f x
y
S(x)-первообразная f(x)
F(x)=S(x)+C-∀ первообразная f(x)
0 a
x
S a 0;
S b S ;
b x
x x
S(x)=F(x)-C
S(a)=F(a)-C=0 C=F(a)
S(x)=F(x)-F(a)
b
S=S(b)=F(b)-F(a)
S f x dx F b F a F x
a
b
a
8.
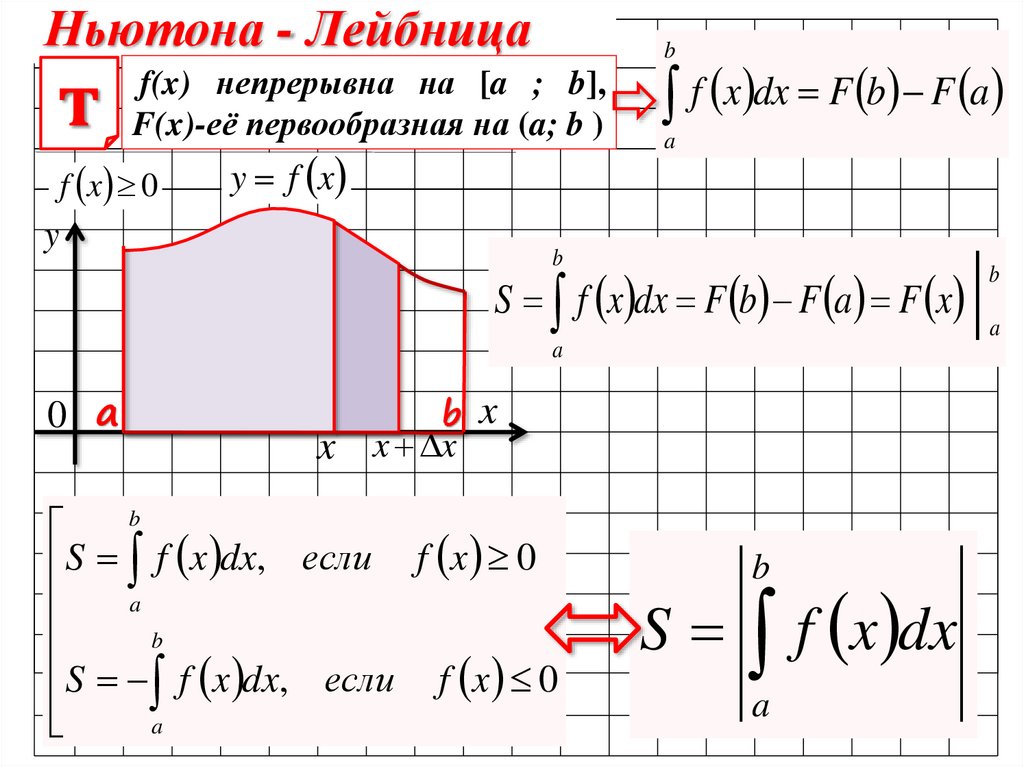
Ньютона - Лейбницат
b
f(x) непрерывна на [a ; b],
F(x)-её первообразная на (a; b )
f x 0
y f x
y
f x dx F b F a
a
b
S f x dx F b F a F x
a
0 a
x
b x
x x
b
S f x dx, если f x 0
a
b
S f x dx, если f x 0
a
b
S f x dx
a
b
a
9.
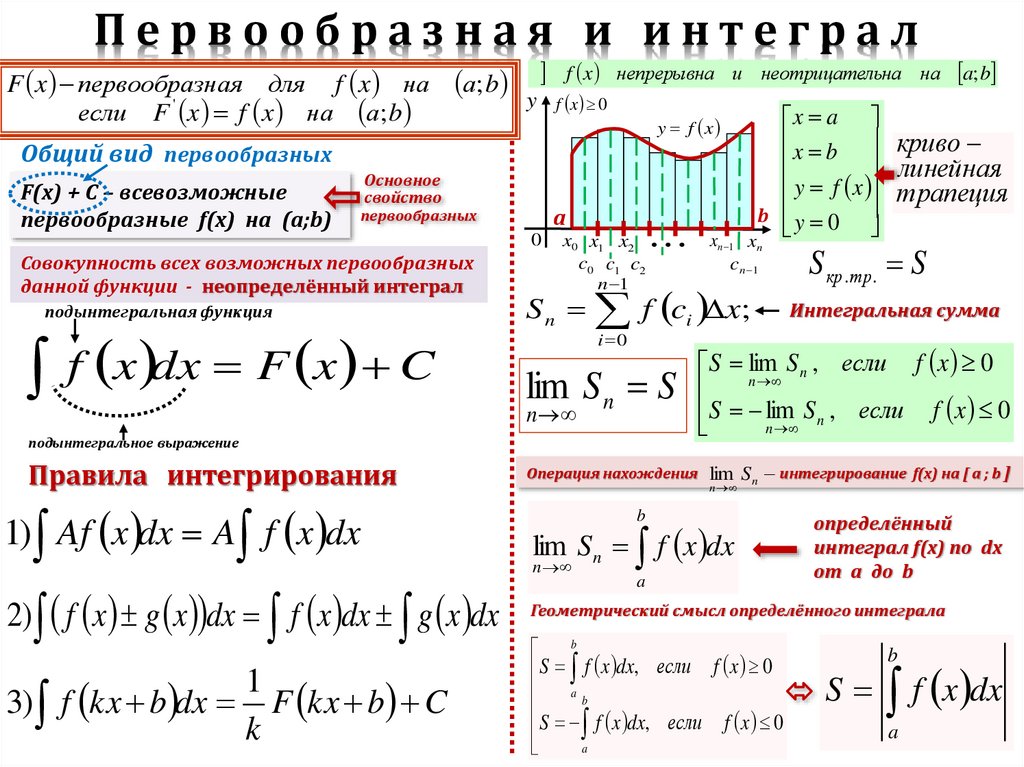
Первообразная и интегралF x первообразная для f x на
если F ' x f x на а; b
а; b y f x непрерывна и неотрицательна на a; b
f x 0
y f x
Общий вид первообразных
F(x) + C – всевозможные
первообразные f(x) на (а;b)
Основное
свойство
a
первообразных
0
Совокупность всех возможных первообразных
данной функции - неопределённый интеграл
подынтегральная функция
f x dx F x C
x0 x1 x2
c0 c1 c2
n 1
x cx
1) Af x dx A f x dx
2) f x g x dx f x dx g x dx
1
3) f kx b dx F kx b C
k
n
n 1
S n f ci x;
i 0
lim S n S
n
подынтегральное выражение
Правила интегрирования
n 1
x a
x b криво
линейная
y f x трапеция
b y 0
Операция нахождения
Интегральная сумма
S lim S n , если f x 0
n
S n , если f x 0
S lim
n
lim S n интегрирование f(x) на [ a ; b ]
n
b
lim S n f x dx
n
S кр .тр. S
a
определённый
интеграл f(x) по dx
от a до b
Геометрический смысл определённого интеграла
b
S f x dx, если f x 0
ab
S f x dx, если f x 0
a
b
S f x dx
a
10.
тНьютона - Лейбница
b
f x dx F b F a
f(x) непрерывна на [a ; b],
F(x)-её первообразная на (a; b )
Cвойства
определённого интеграла
a
a
Вычисление площадей плоских фигур
с помощью определённого интеграла
1) f x dx 0
y
y
y f x
a
b
a
a
b
2) f x dx f x dx
0
b
b
b
a
b
b
a
a
y f x
b
b
a
a
a
a
y
y
y f x
y f x
y
y f x
4) kf x dx k f x dx
b
c
x
a
b
5) f x dx f x dx f x dx
a
a
a c b
b
S f x dx S f x dx S f x dx
b
3) f x g x dx f x dx g x dx
a
x
0
x
a
b
a
c
y g x
a
0
x
0
b
x
a
y g x
b
b
S f x g x dx
a
0
b
y g x
11.
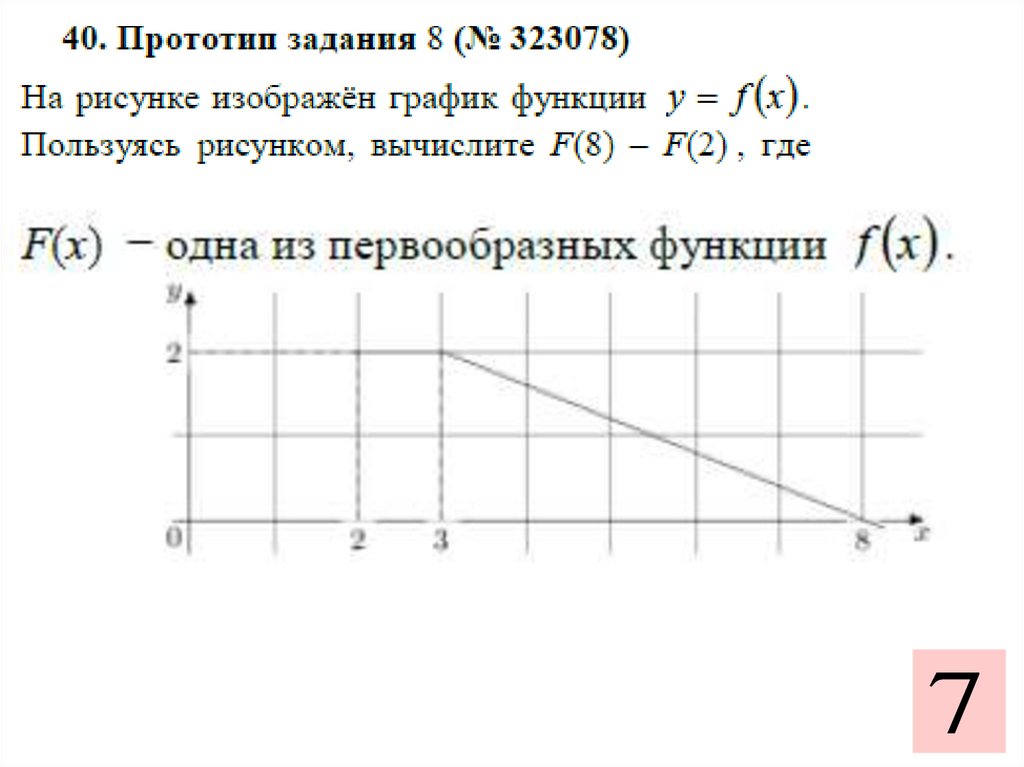
712.
2№1. Вычислите
2
x
dx
0
13.
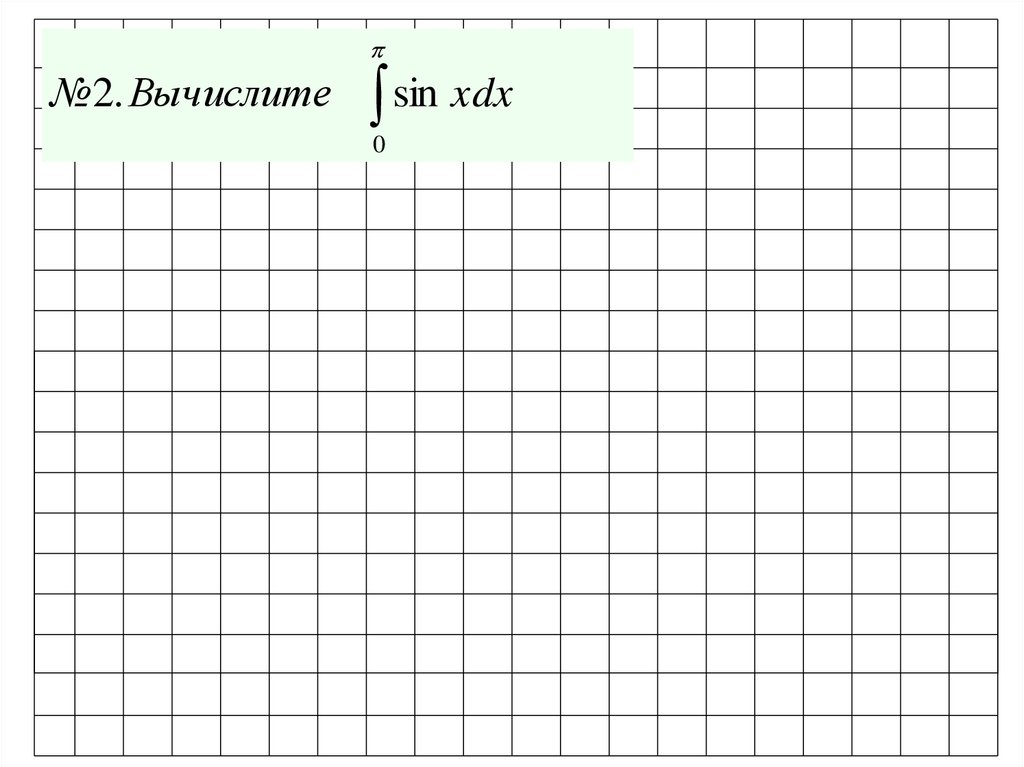
№2. Вычислитеsin xdx
0
14.
0№3. Вычислите
sin xdx
15.
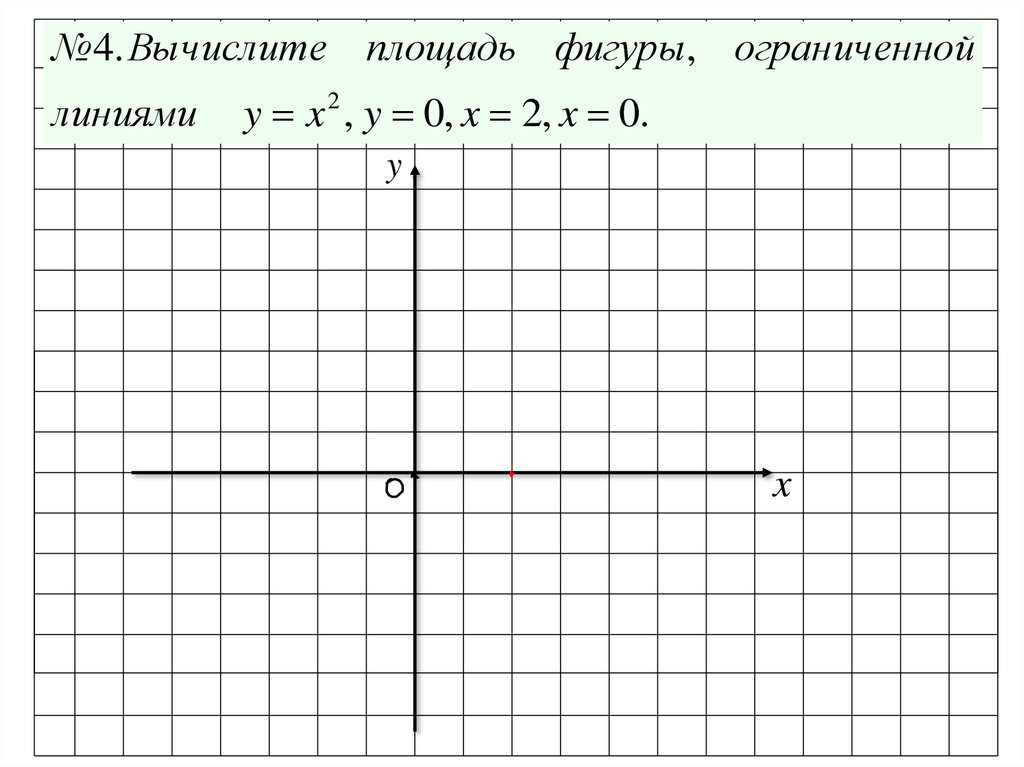
№4. Вычислите площадь фигуры, ограниченнойлиниями
y x 2 , y 0, x 2, x 0.
y
x
16.
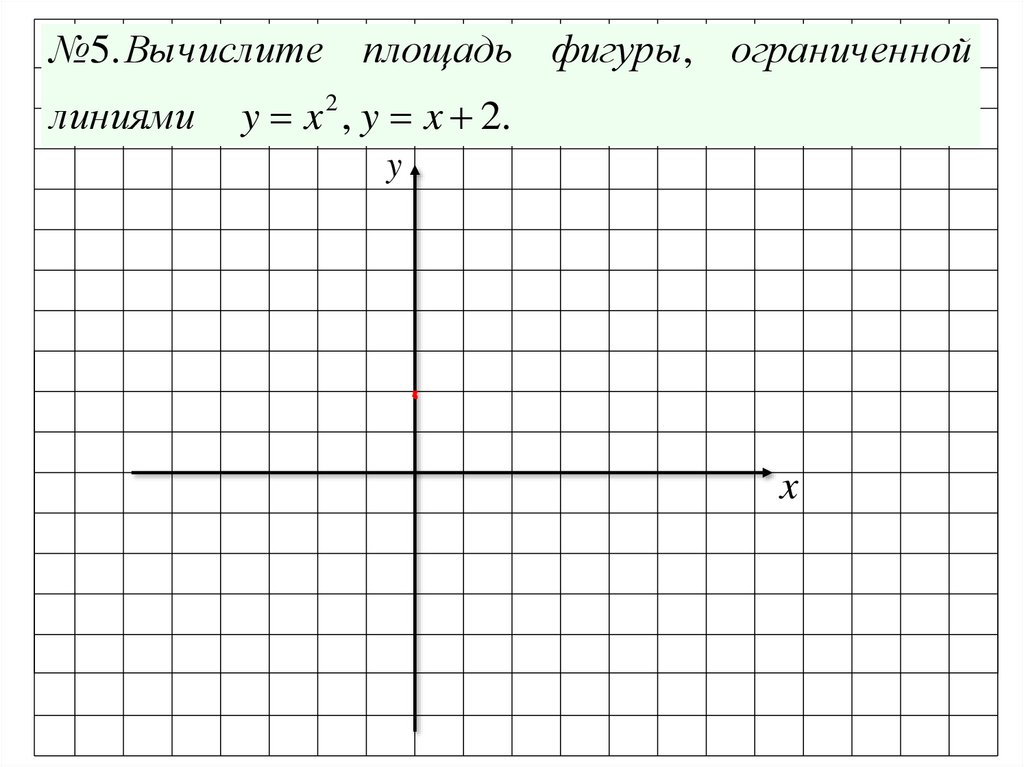
№5. Вычислите площадь фигуры, ограниченнойлиниями
y x 2 , y x 2.
y
x
17.
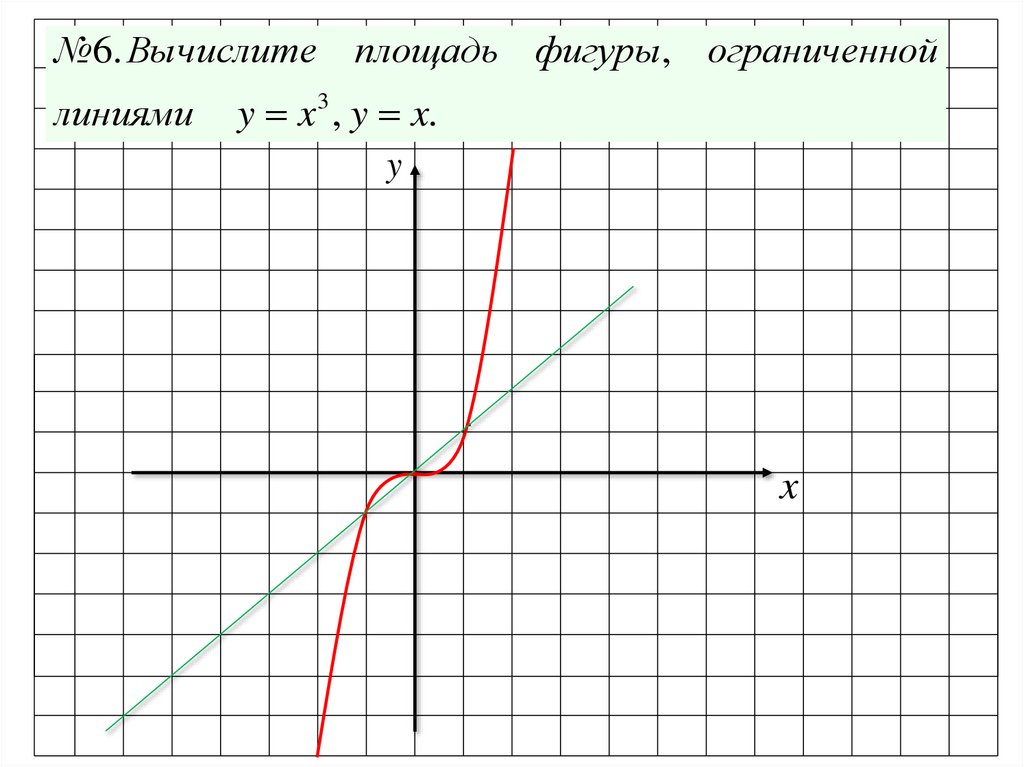
№6. Вычислите площадь фигуры, ограниченнойлиниями
y x 3 , y x.
y
x
18.
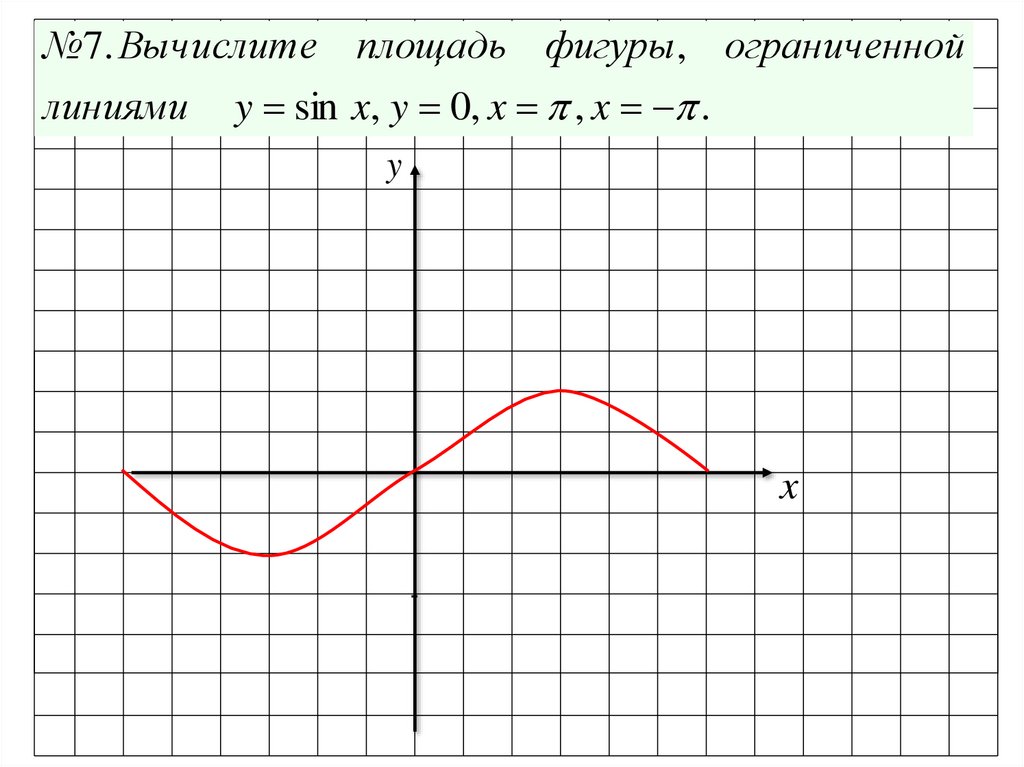
№7. Вычислите площадь фигуры, ограниченнойлиниями y sin x, y 0, x , x .
y
x
19.
№8. Вычислите площадь фигуры, ограниченнойлиниями
y x 3 , y 0, x 1.
y
x
20.
№9. Вычислите площадь фигуры, ограниченнойлиниями
y x 2 0, y 2 x 0.
y
x
21.
№10. Вычислите площадь фигуры, ограниченнойлиниями
y x 2 , y 0, x 0, x 2.
y
x
22.
№11. Вычислите площадь фигуры, ограниченнойлиниями
y x 2 , y 0, x 3, x 5.
y
x
23.
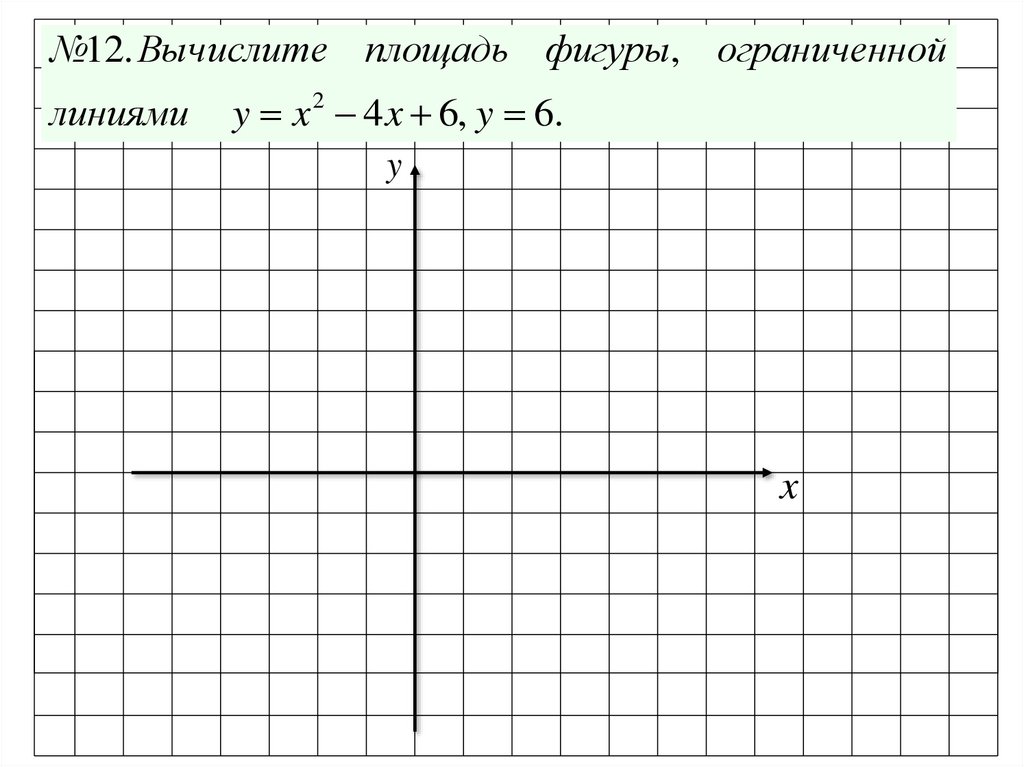
№12. Вычислите площадь фигуры, ограниченнойлиниями
y x 2 4 x 6, y 6.
y
x
24.
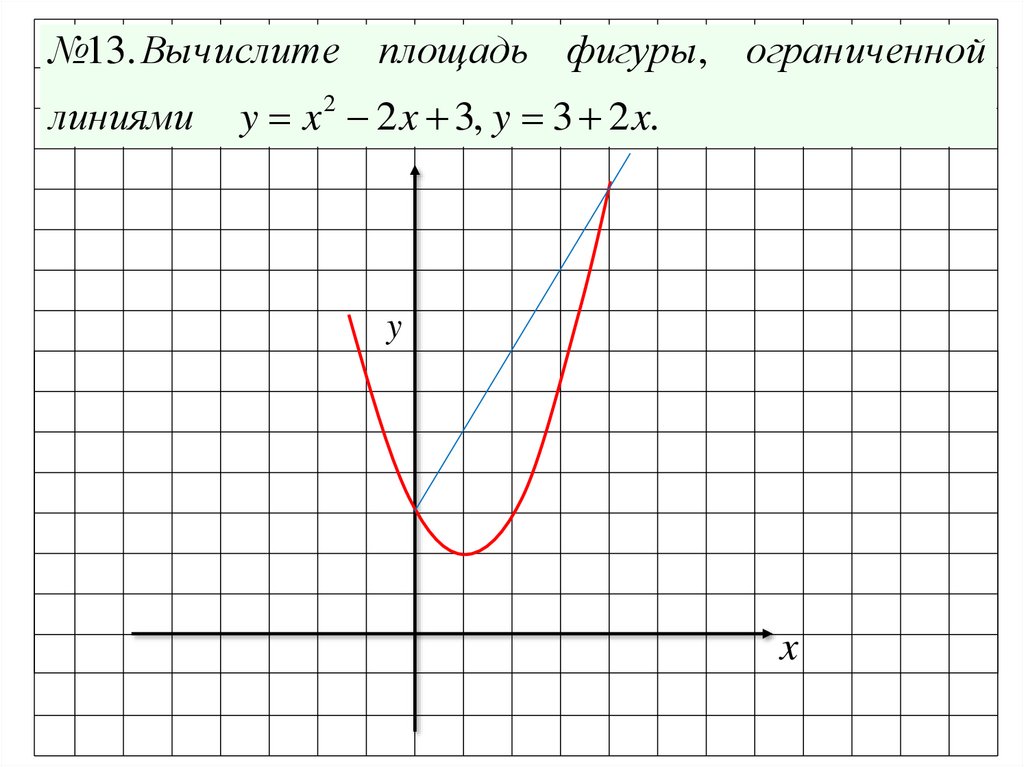
№13. Вычислите площадь фигуры, ограниченнойлиниями
y x 2 x 3, y 3 2 x.
2
y
x
25.
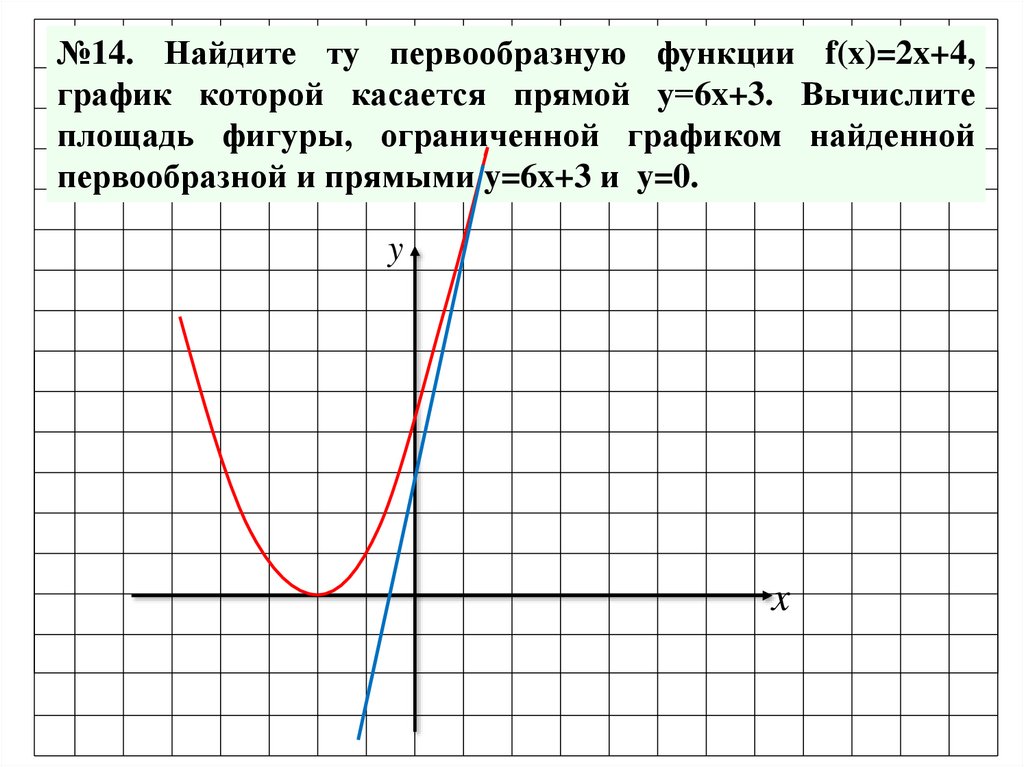
№14. Найдите ту первообразную функции f(x)=2x+4,график которой касается прямой у=6x+3. Вычислите
площадь фигуры, ограниченной графиком найденной
первообразной и прямыми y=6x+3 и y=0.
y
x
26.
Домашнеезадание на
25.12.23г

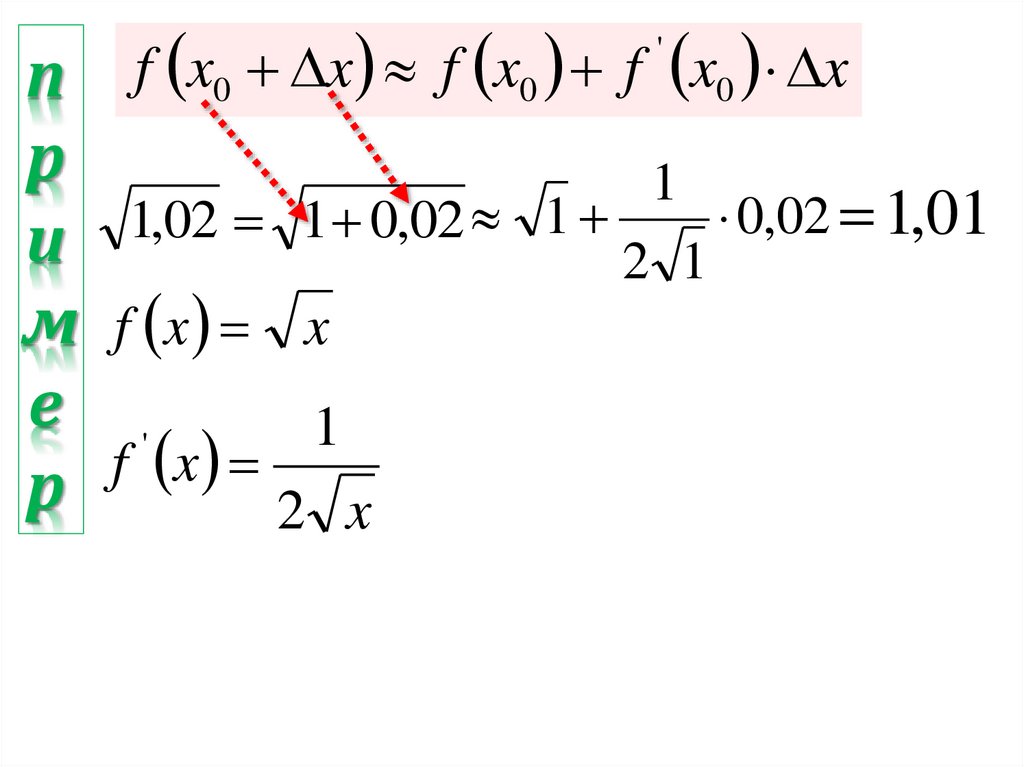








 Математика
Математика








