Похожие презентации:
Интеграл. Формула Ньютона-Лейбница
1.
2.
Цель урока:Ввести понятие интеграла и его вычисление по
формуле Ньютона – Лейбница, используя знания о
первообразной и правила её вычисления;
Проиллюстрировать практическое применение
интеграла на примерах нахождения площади
криволинейной трапеции;
Закрепить изученное в ходе выполнения
упражнений.
3.
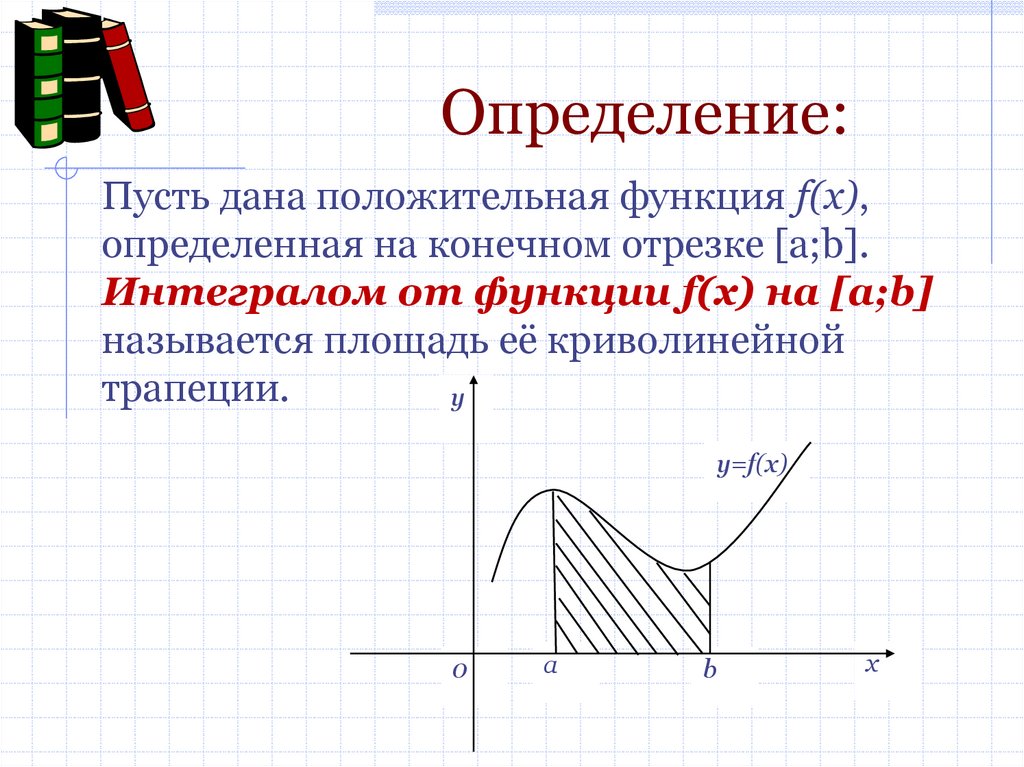
Определение:Пусть дана положительная функция f(x),
определенная на конечном отрезке [a;b].
Интегралом от функции f(x) на [a;b]
называется площадь её криволинейной
трапеции.
y
y=f(x)
0
a
b
x
4.
Обозначение:«интеграл от a до b эф от икс дэ
икс»
5.
Формула Ньютона - Лейбница6.
Пример 1.Вычислить определённый интеграл:
Решение:
=
7.
Пример 2.Вычислите определённые интегралы:
5
9
1
8.
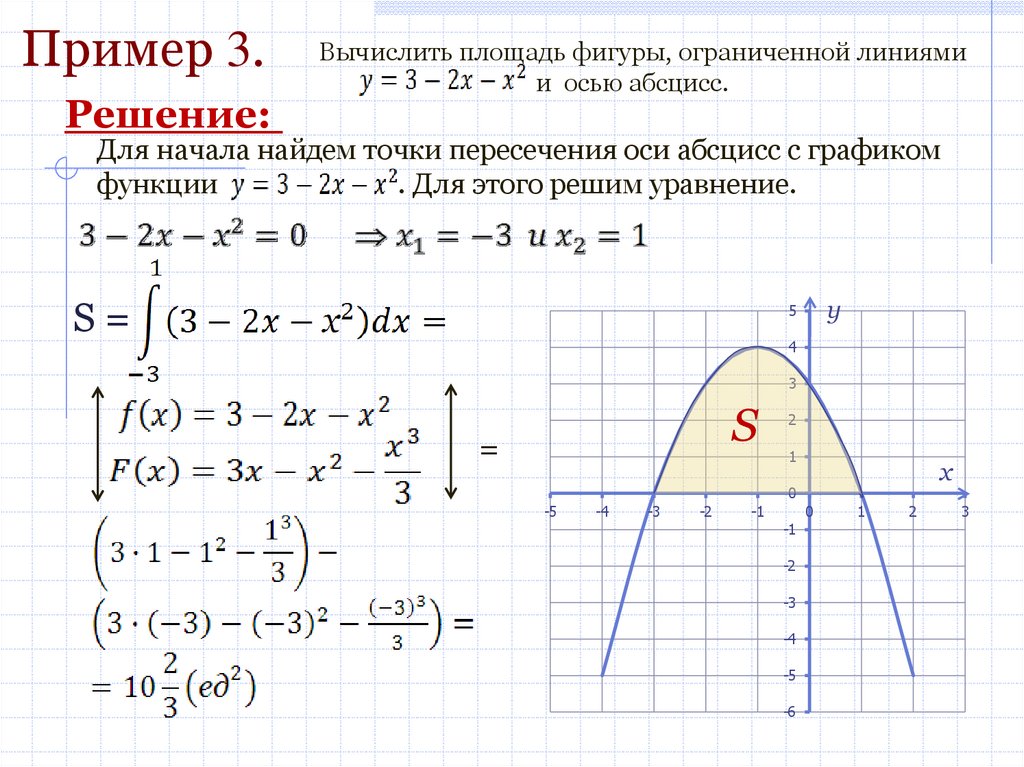
Пример 3.Решение:
Вычислить площадь фигуры, ограниченной линиями
и осью абсцисс.
Для начала найдем точки пересечения оси абсцисс с графиком
функции
. Для этого решим уравнение.
S=
y
5
4
3
S
=
2
1
x
0
-5
-4
-3
-2
-1
0
-1
-2
-3
-4
-5
-6
1
2
3
9.
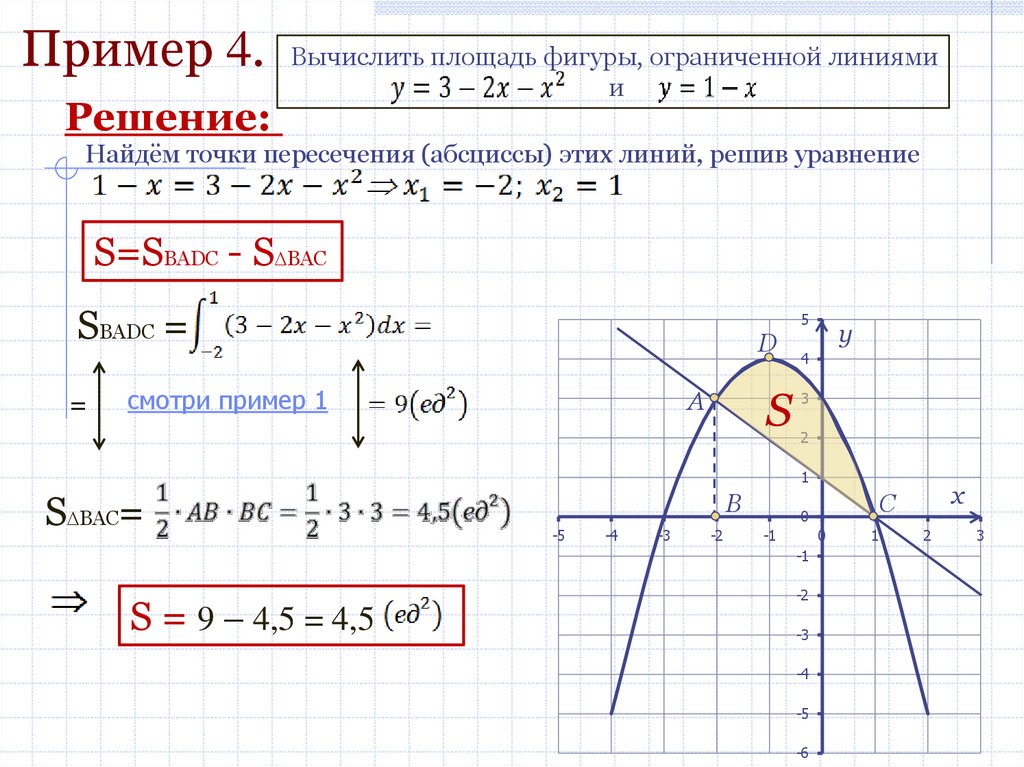
Пример 4.Решение:
Вычислить площадь фигуры, ограниченной линиями
и
Найдём точки пересечения (абсциссы) этих линий, решив уравнение
S=SBADC - S BAC
SBADC =
=
5
D
смотри пример 1
S
A
y
4
3
2
1
S BAC=
B
-5
-4
-3
-2
-1
0
-1
S = 9 – 4,5 = 4,5
-2
-3
-4
-5
-6
x
C
0
1
2
3
10.
« ТАЛАНТ –это 99% труда и 1% способности»
народная мудрость







 Математика
Математика








