Похожие презентации:
Решение уравнений. 9 класс. Подготовка к государственной итоговой аттестации
1.
Решениеуравнений
9 класс
Подготовка к государственной
итоговой аттестации
2. Цель урока: отработка предметного навыка решения рациональных уравнений в формате ОГЭ.
«Решение труднойматематической проблемы
можно сравнить со
взятием крепости»
Н.Я.Виленкин
Цель урока:
отработка предметного навыка
решения рациональных
уравнений в формате ОГЭ.
3. Установите соответствие между выражением и значением выражения.
АБ
В
2
1
4
4.
5. Корни уравнения – это значение переменной при которой уравнение становится верным равенством Решить уравнение – это значит
Уравнение- это равенствосодержащее переменную.
Корни уравнения – это значение
переменной при которой уравнение
становится верным равенством
Решить уравнение – это значит
найти все его корни.
6. Уравнения: линейные уравнения; квадратные уравнения; биквадратные уравнения; дробно-рациональные уравнения кубические уравнения
Уравнения:линейные уравнения;
. квадратные уравнения;
биквадратные уравнения;
дробно-рациональные
уравнения
кубические уравнения
(уравнения третей степени)
7. Линейное уравнение – это уравнение вида ах+в=0, a(x+b)=0 Алгоритм решения: Раскрыть скобки. Перенести слагаемые с переменными в
Линейное уравнение – этоуравнение вида ах+в=0,
.
a(x+b)=0
Алгоритм решения:
Раскрыть скобки.
Перенести слагаемые с
переменными в одну
сторону, а без переменных в
другую и найти неизвестное.
8.
Сколько корней может иметьлинейное уравнение ax=-b ?
b
1) при a 0 x ,
a
2) при a 0, b 0 0 x 0, x R,
3) при a 0, b 0 0 x b,
уравнение не имеет корней .
9. Квадратные уравнения- это уравнения вида ax²+bx+c=0
.Виды квадратных уравнений:
1) Неполное квадратное
уравнение
а) ax²+bx=0
b) ax²+c=0
2) Полное квадратное
уравнение:
ax²+bx+c=0
10.
Квадратныеуравнения:
D b 4ac
2
ax2+bx+c=0
x1, 2
b D
2a
Неполные квадратные уравнения:
2+c=0
ax
2
ax +bx=0
c
x(ax+b)=0
x=
,
a
x=0 или (ax+b)=0
где ас<0.
x=-b:a
11. Дробно – рациональные уравнения:
Aприводятся к виду : 0,
B
где A, B многочлены, B 0.
Алгоритм решения дробно-рационального
уравнения:
1)
найти общий знаменатель дробей, входящих в
уравнение;
2) умножить обе части уравнения на общий
знаменатель;
3) решить получившееся целое уравнение;
4) исключить из его корней те, которые обращают
в нуль общий знаменатель.
12.
Уравнение вида ax4
bx c 0
2
,
где
а, b, c – данные числа и а отлично от
нуля, а х –неизвестное, называют
биквадратным уравнением.
Чтобы решить биквадратное уравнение, вводят
новую переменную у = х2
Тогда исходное уравнение превращается в
2
квадратное ay by c 0 относительно
неизвестного y.
13.
Кубическое уравнение – алгебраическоеуравнение третьей степени.
Общий вид кубического уравнения:
ax³+bx²+cx+d=0, где a≠0
Пример:
х³+2x²-x-2=0
x²(х+2) – (х+2)=0
(х+2)(x²-1)=0
(х+2)(х-1)(х+1)=0
х=-2; х=-1; х=1
14.
1) 5х = 7 имеетединственный корень.
2) 0х = 0 не имеет корней.
3) Если Д > 0, то квадратное
уравнение имеет два корня.
4) Если Д < 0, то квадратное
уравнение имеет 1 корень.
5) Количество корней не
больше степени уравнения.



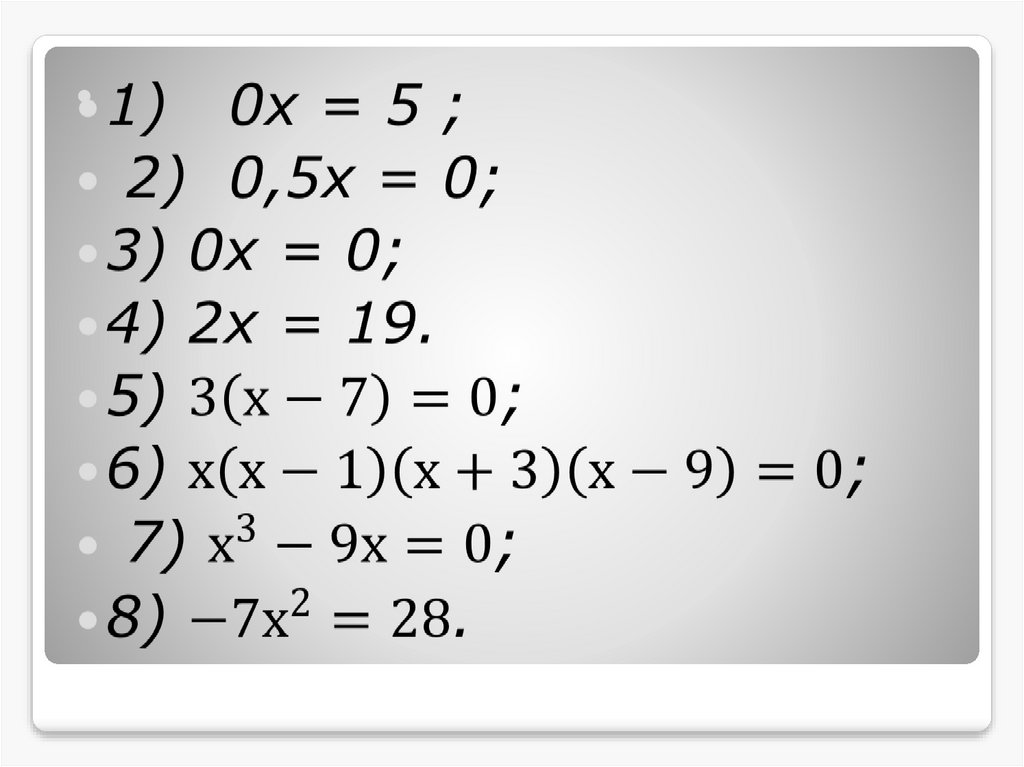










 Математика
Математика








