Системы счисления. Числа и цифры

1. Системы счисления

Когда речь идет о чем-нибудь очень простом,
понятном, мы часто говорим: «Дело ясно,
как дважды два –четыре!»
О том, как люди научились считать и мерить, откуда появились
числа, а следовательно и системы счисления расскажет эта
презентация.

2. Числа и цифры

Проходили многие и многие годы. Менялась жизнь человека. Появилось
скотоводство, начало развиваться земледелия. Постепенно росли знания
людей, тем больше возникало потребность в умении считать и мерить.
Счет времени по лунным месяцам уже не годился. Все чаще люди
сталкивались с большими числами, которые было трудно запомнить.
Первая запись чисел – это зарубки на палке. Если небольшое число, то
сосчитать зарубки несложно, а если нет, то это требовало больших затрат
времени. Очень неудобная «запись!»
И вот примерно пять тысяч лет назад одновременно в разных странах,
регионах – Вавилонии, Египте, Китае, Греции, Центральной Америке –
родился новый способ записи чисел.
Люди додумались до того, что числа можно записывать не просто
зарубками-единицами, а по разрядам: отдельно единицы, отдельно
десятки, отдельно сотни. Это стало очень важным открытием.

3. Египет

Древние египтяне считали десятками. Но специальные
значки-цифры у них были только для разрядов: единиц,
десятков, сотен, тысяч.
Например, чтобы записать нашу цифру семь,
египтянину приходилось рисовать семь палочек

4. Вавилон

В Древнем Вавилоне считали не десятками,
шестидесятками. Значит система счисления у них была не
десятичная, а шестидесятеричная. Число шестьдесят у
них играло такую же роль, как у нас десять. Например,
число 137 вавилонский ученый представлял так:
2 шестидесятки +17 единиц = 137
Вавилоняне использовали всего две цифры. Вертикаль
черточка обозначала одну единицу, а угол из двух лежачих
черточек – десять. Черточки получались в виде клиньев,
т.к. они писали острыми папочками на глиняных досках.
Эта запись чисел требовала много времени.
Но все же в настоящее время мы пользуемся вавилонской
системой счета: в часе 60 минут, в минуте - 60 секунд.

5. Народы майя

майя
Народы
Майя считали двадцатками- у них была
двадцатеричная система счета. Числа
от 1 до 20 обозначались точками и
черточками. Если под числом был
нарисован особый значок в виде глаза,
это означало,что число надо увеличить
в двадцать раз, получались не
единицы. А двадцатки, второй разряд.
Например , число 45 майя записывали
так:
Если глаз был нарисован дважды, то число надо было дважды умножить на
двадцать, Это был третий разряд – четырехсотки. Изображение глаза у майя
выполняло роль цифры нуль. Только они рисовали глаз не рядом, а под числом.

6. Китай

Китайцы пользовались десятичной системой
счета.
Если справа от цифры стоит значок «10», - значит,
цифру надо умножить на10. Получаются десятки,
второй разряд. Например, число 1492 по-китайски
надо записать так:

7. Древняя Греция

Греки записывали числа буквами. Эта был не очень
удобный способ. Невозможно было выполнять сложение
столбиком.

8. Древние счеты

Поэтому придумали счетный столбик – абак. Доска разделена на
вертикальные полоски. Каждая
полоса предназначена для
откладывания отдельных
разрядов чисел. Полоски
соединены дужками по три в
классы: единицы, тысячи,
миллионы.
На абаке отложено число
Наши счеты –это прообраз абака, только
510 742
вместо полосок, проволока и бусины.
Перуанский веревочный абак,
«квипос». Однократно
завязанный узел на веревке – 10,
двукратно -100 и т.д.
Семикосточковые счеты,
распространенные в Китае и Японии

9. Древний Рим

Две тысячи лет назад, во все страны о которые покорили
древние римляне приносили с собой свой язык, культуру,
свои порядки и законы. Единственное наследие, которым
мы пользуемся до сих пор – это латинский язык (для
врачей, ученых) и римские цифры.

10. Древняя Индия

Индийцы изобрели позиционную
систему счисления – тот способ
записи и чтения чисел, которым
теперь пользуется весь мир.
Каждый разряд обозначался
отдельным словом, для сотен свое,
для миллионов другое. Сколько цифр,
столько слов. Это было громоздко и
индийцы стали поступать иначе. Стали
просто называть цифры, а если это
был нуль – говорили «пусто» или
ставили точку. Позднее стали вместо
точки рисовать кружок. Такой кружок
назывался «сунья»( на языке хинди –
«пусто», «пустое место»).
Индийские цифры
Индия была оторвана от других стран,
- на пути лежали тысячи км и высокие
горы. Поэтому математические
изыскания не стали так известны миру.

11. Свет с востока

Арабы были первооткрывателями в мире точных наук.
Они собрали все наследие Индии, Китая и представили
миру достижения древних ученых.
Арабские математики перевели слово «сунья» по смыслу
на свой язык и получилось слово «сифр». Это знакомое
нам слово досталось по наследству от арабов и
превратилось в слово «цифра». Взяв за основу
индийский цифры арабы создали свой ряд цифр,
которыми мы пользуемся и сейчас.
Сейчас цифрами называются все десять значков для
записи чисел. Но еще двести лет назад цифрой в русском
языке назывался один-единственный значок –нуль.
Современное слово «нуль» родилось недавно. Имеет
происхождение от латинского слова «никакая».
Арабские цифры

12. Древняя Русь

В Х веке нашего летосчисления у
славян появилась письменность.
С этого момента начинается
«писаная» история Древней Руси.
Развитие торговли дало
возможность общаться с
различными народностями и
перенимать знания во всех
областях. Так основу алфавита –
от византийцев. Способ записи
цифр буквами со специальными
значками – «титлами» - от греков.
Запись больших
чисел
Славянские цифровые знаки –буквы с титлами

13. Этапы превращения первоначальных цифр в современные

Нынешняя форма цифр установилась после изобретения книгопечатания
в ХV веке.

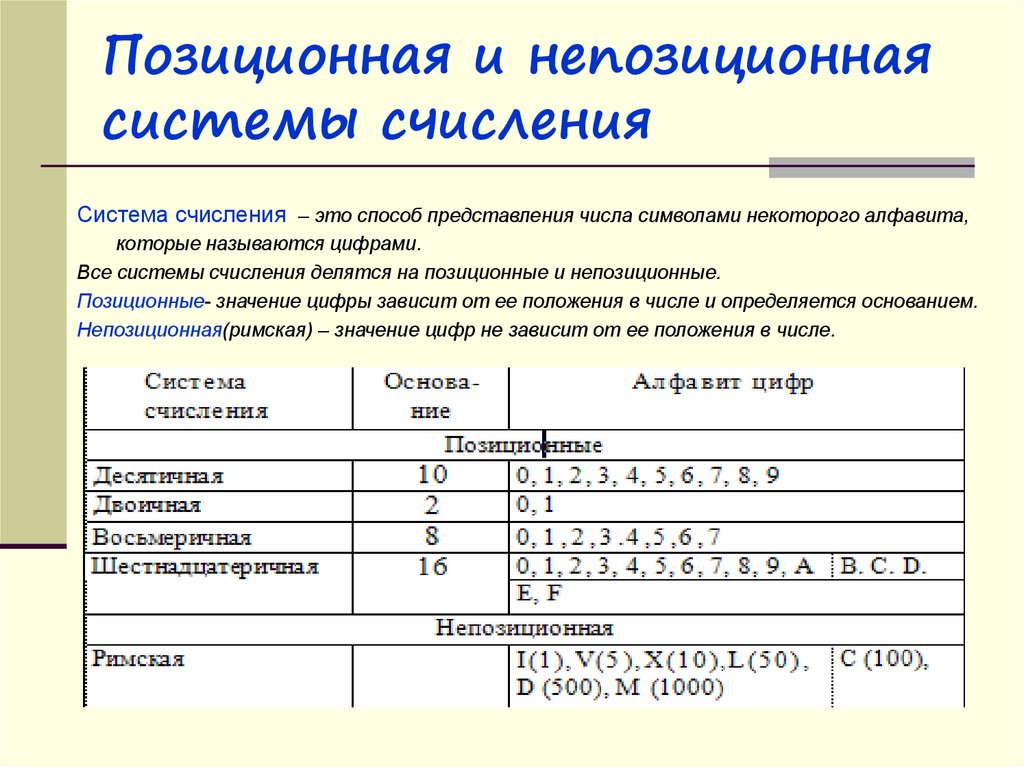
14. Позиционная и непозиционная системы счисления

Система счисления – это способ представления числа символами некоторого алфавита,
которые называются цифрами.
Все системы счисления делятся на позиционные и непозиционные.
Позиционные- значение цифры зависит от ее положения в числе и определяется основанием.
Непозиционная(римская) – значение цифр не зависит от ее положения в числе.

15. Двоичная система счисления

Принцип действия компьютера основан на
системе чисел, на двух цифрах: 0 и 1.
0- отсутствие сигнала; 1- наличие сигнала.

16.

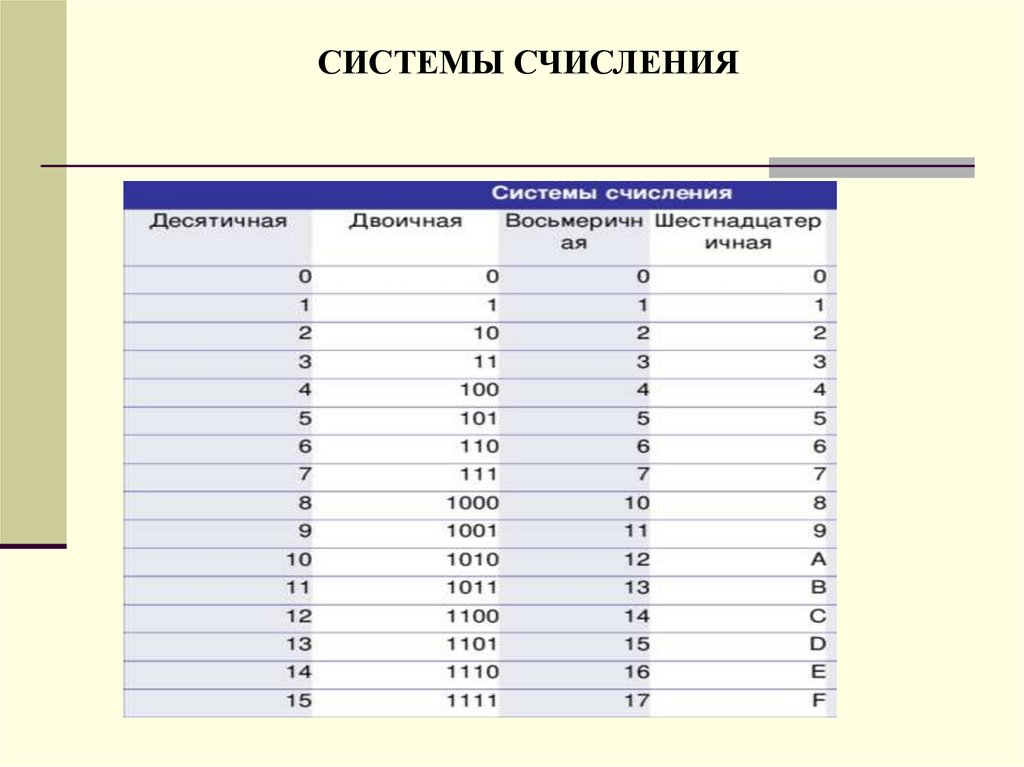
СИСТЕМЫ СЧИСЛЕНИЯ

17.

Соотношение 10-тичной, двоичной, 8-ричной, 16-ричной систем
представим двоичное число
10101101011112
в 8-ричной системе счисления,
1 010 110 101 111
1 2 6 5 7
100 0112=438
1000 10102=8А16

18.

Перевод чисел из позиционной СС с основанием q в десятичную
систему счисления

19.

Перевод чисел из позиционной СС с основанием q в десятичную
систему счисления

20.

21. Общее правило перевода из одной системы счисления в другую

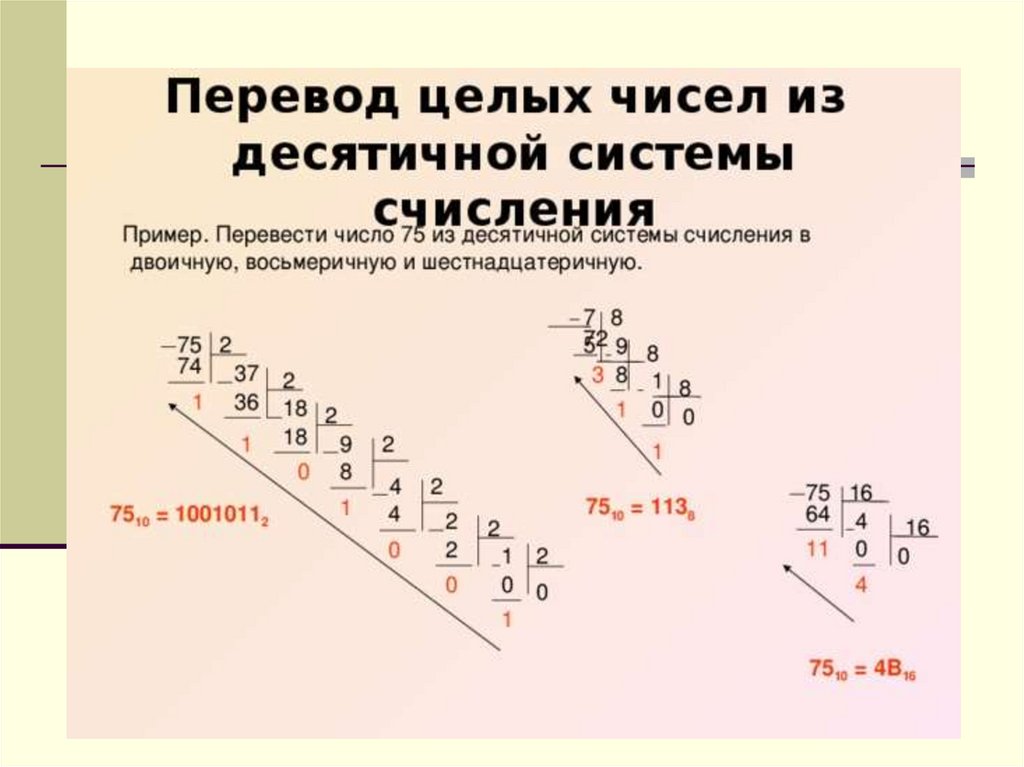
Перевод целого числа из системы счисления с основанием S в другую
систему счисления с основанием q осуществляется последовательным
делением его основания q новой системы счисления до тех пор, пока не
получится частное, меньшее q. Число в новой системе запишется в виде
остатков деления, начиная с последнего.
ПРИМЕР
37710 в двоичную систему 1011110012

22.

23.

Перевести следующие числа в
десятичную систему счисления:
XXIV=
MCDXXII=
XIV=
123,2458=
2222,13=
6548,4D16=
10111,12=
1101,0012=
1010,112=
D1,F16=
333,436=
222,124=