Аксиомы стереометрии

1. Аксиомы стереометрии

Геометрия. Урок № 1
10 класс
Евклид
Если теорему так и не смогли
доказать, она становится аксиомой

2. Геометрия

Планиметрия
Стереометрия
stereos - телесный, твердый, объемный, пространственный
metreo - измерять

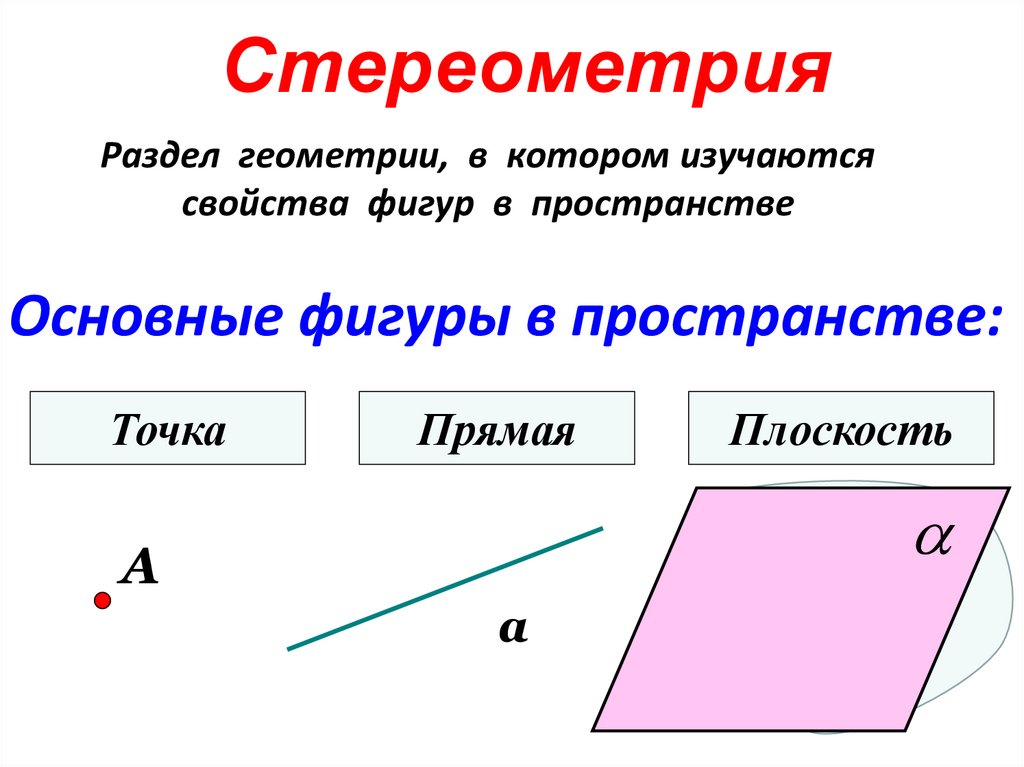
3. Стереометрия

Раздел геометрии, в котором изучаются
свойства фигур в пространстве
Основные фигуры в пространстве:
Точка
Прямая
Плоскость
А
а

4.

A, B, C, …
или
a, b, c, …
AВ, BС, CD, …
, , ,...

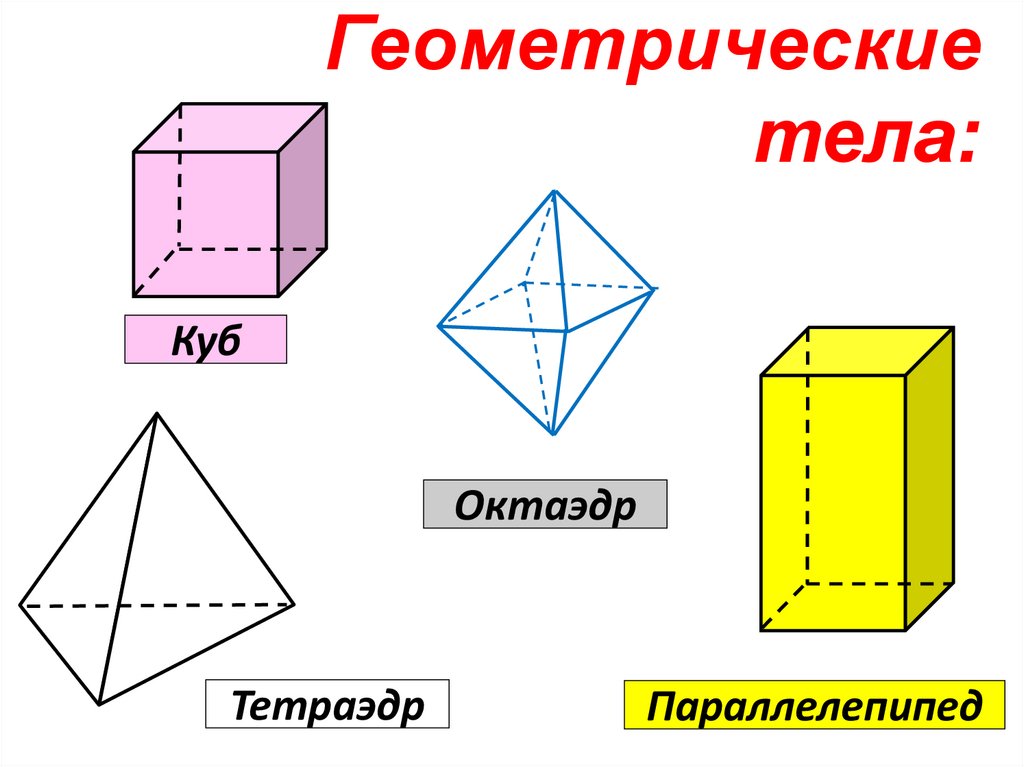
5. Геометрические тела:

Куб
Октаэдр
Тетраэдр
Параллелепипед

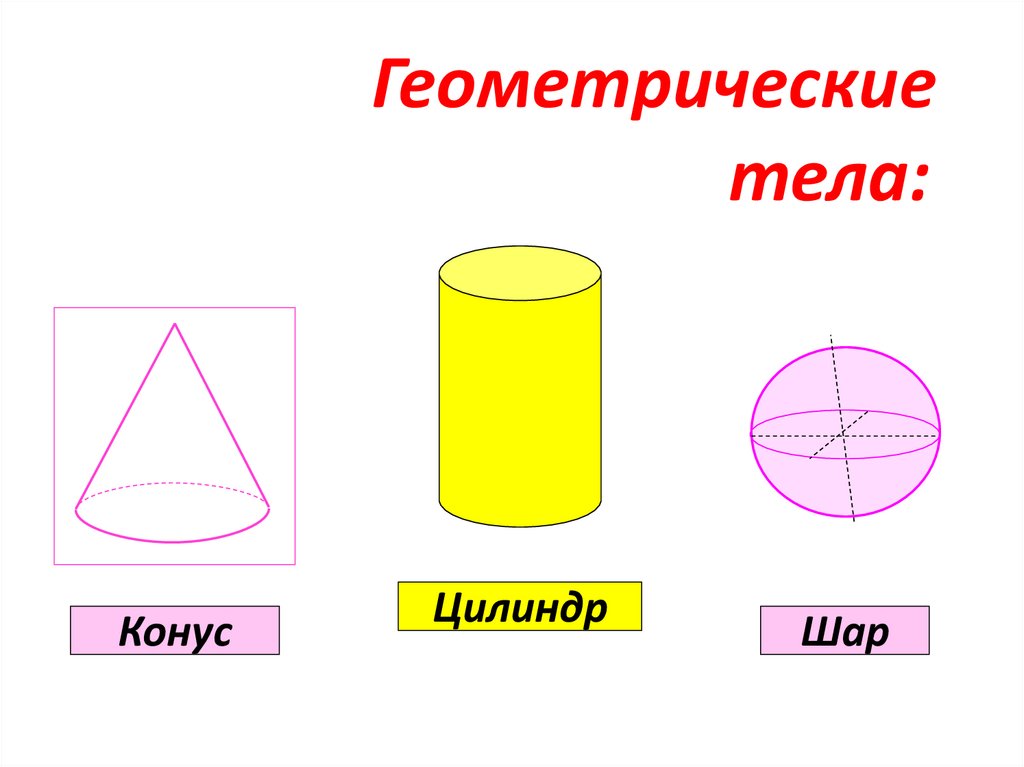
6.

Геометрические
тела:
Конус
Цилиндр
Шар

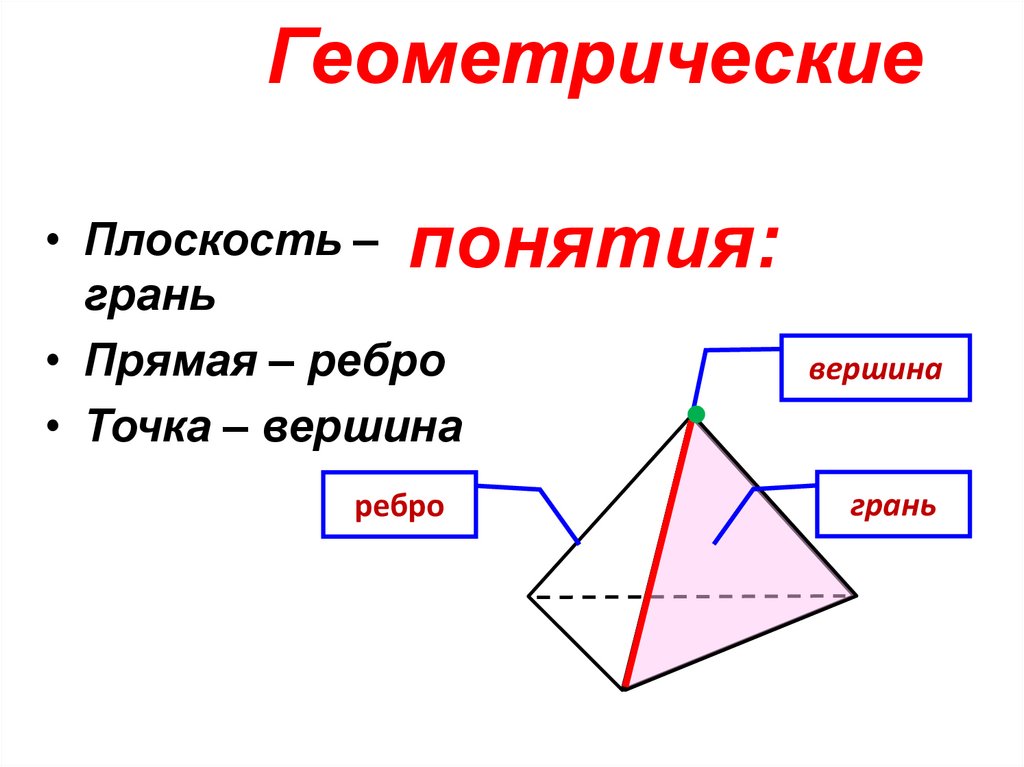
7. Геометрические понятия:

• Плоскость –
грань
• Прямая – ребро
• Точка – вершина
ребро
вершина
грань

8. Аксиома

(от греч. axíõma – принятие положения)
- исходное положение научной теории,
принимаемое без доказательства "Так называемые аксиомы
математики - это те немногие
мыслительные определения,
которые необходимы в математике
в качестве исходного пункта"
Ф. Энгельс

9.

Аксиомы стереометрии
В
А
С
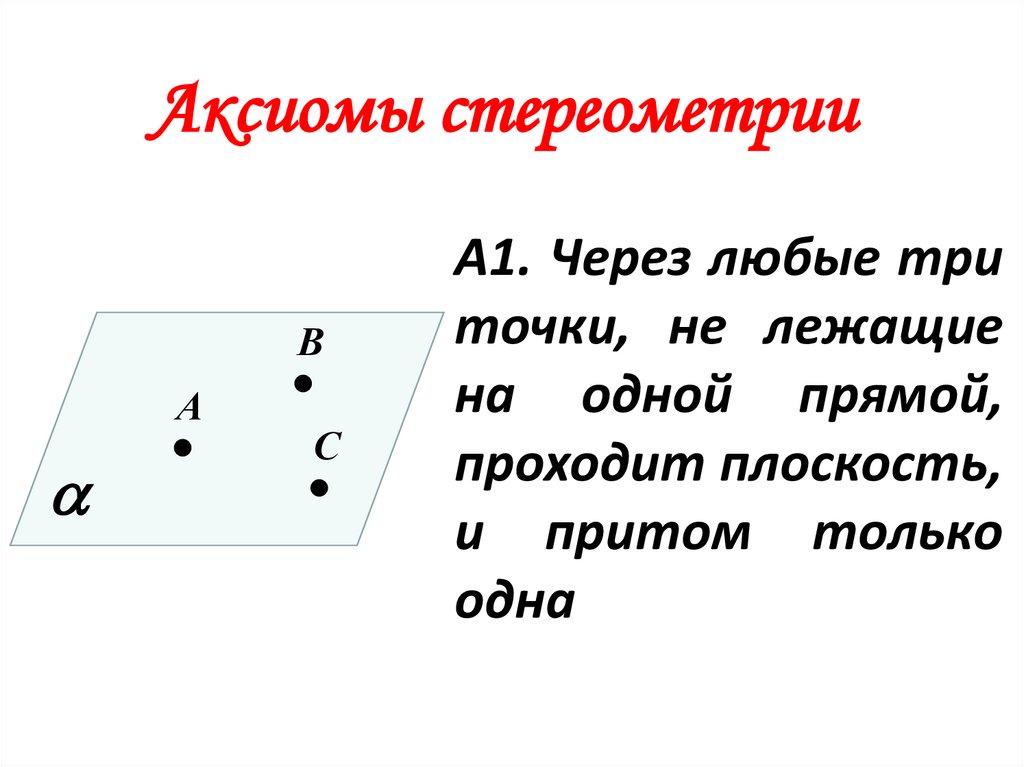
А1. Через любые три
точки, не лежащие
на одной прямой,
проходит плоскость,
и притом только
одна

10.

Аксиомы стереометрии
В
А
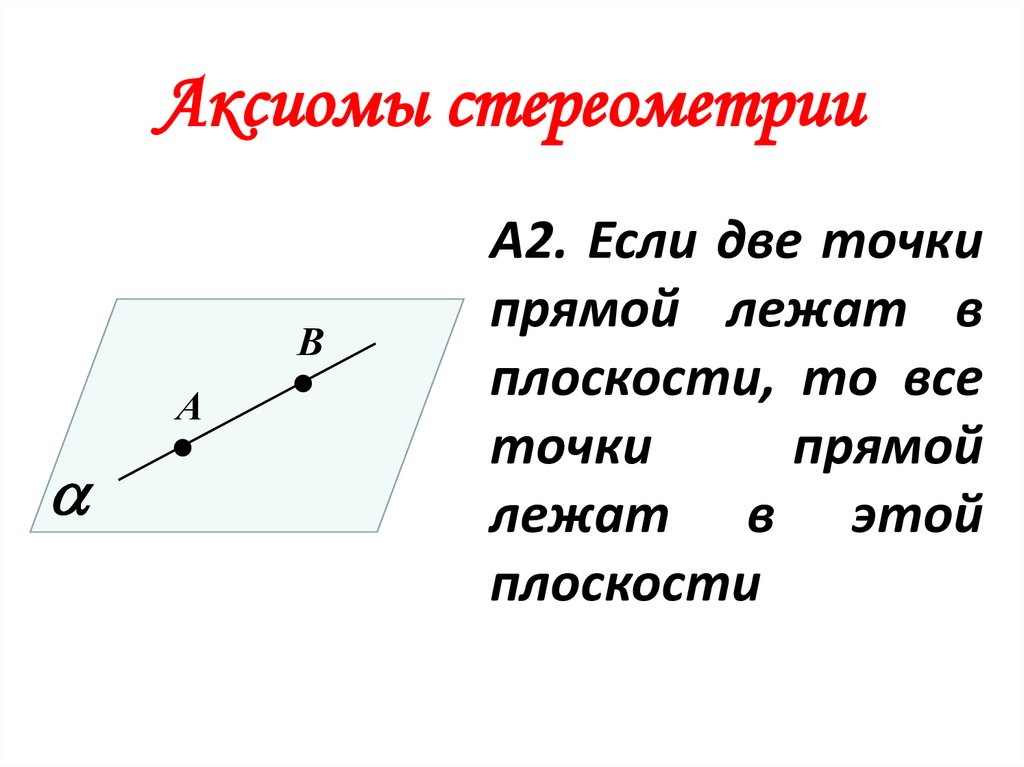
А2. Если две точки
прямой лежат в
плоскости, то все
точки
прямой
лежат в этой
плоскости

11.

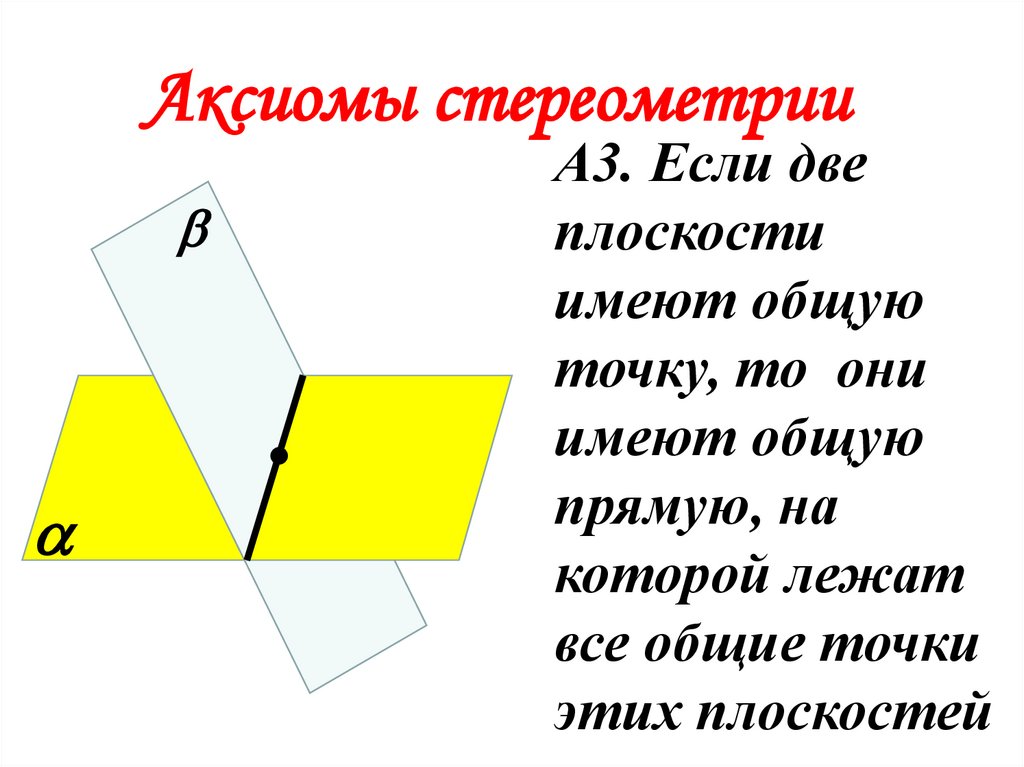
Аксиомы стереометрии
А3. Если две
плоскости
имеют общую
точку, то они
имеют общую
прямую, на
которой лежат
все общие точки
этих плоскостей

12.

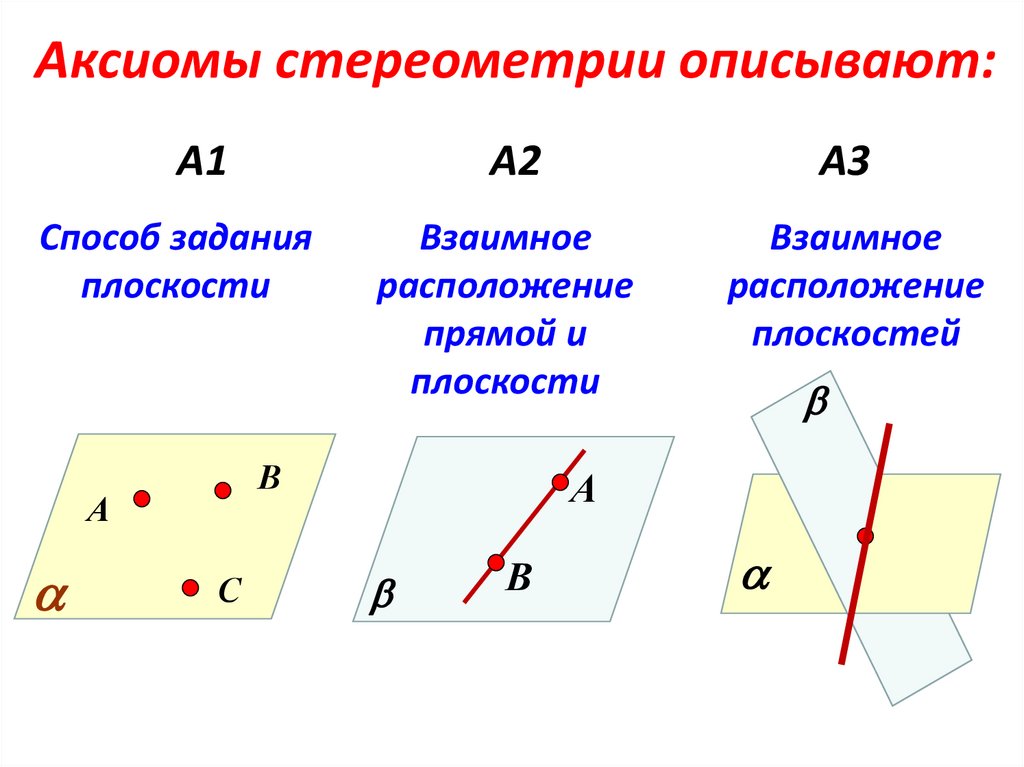
Аксиомы стереометрии описывают:
А1
Способ задания
плоскости
А3
Взаимное
расположение
прямой и
плоскости
Взаимное
расположение
плоскостей
В
А
А2
С
А
В

13.

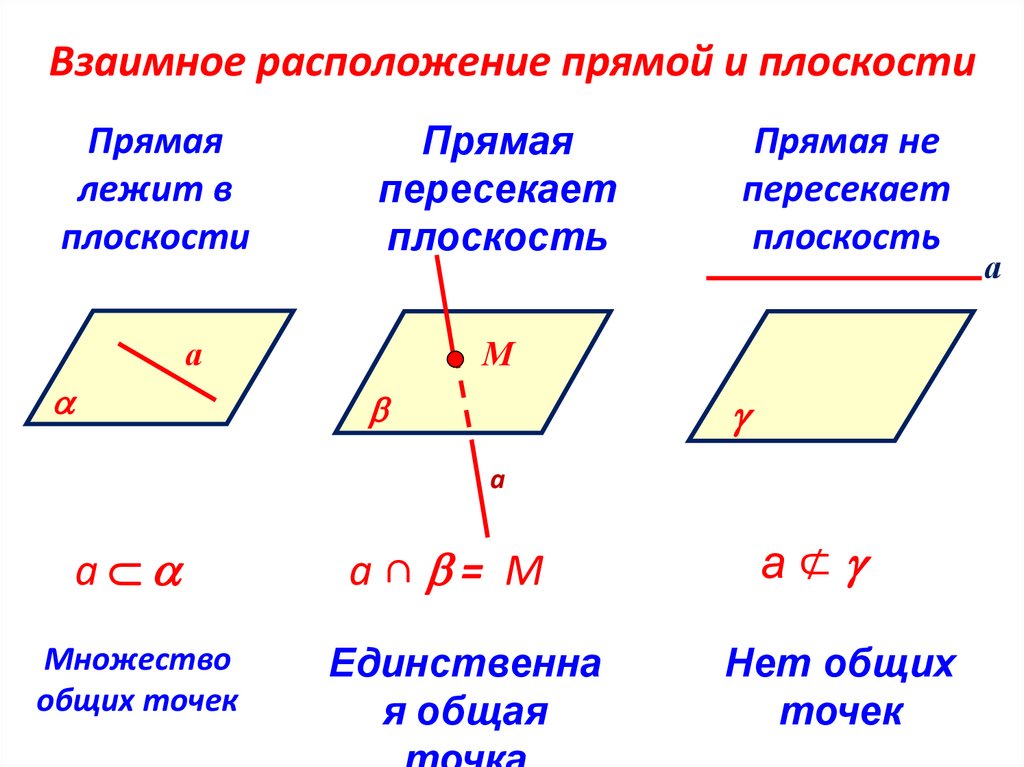
Взаимное расположение прямой и плоскости
Прямая
лежит в
плоскости
Прямая
пересекает
плоскость
а
Прямая не
пересекает
плоскость
М
а
а
Множество
общих точек
а∩ = М
Единственна
я общая
а⊄
Нет общих
точек
а

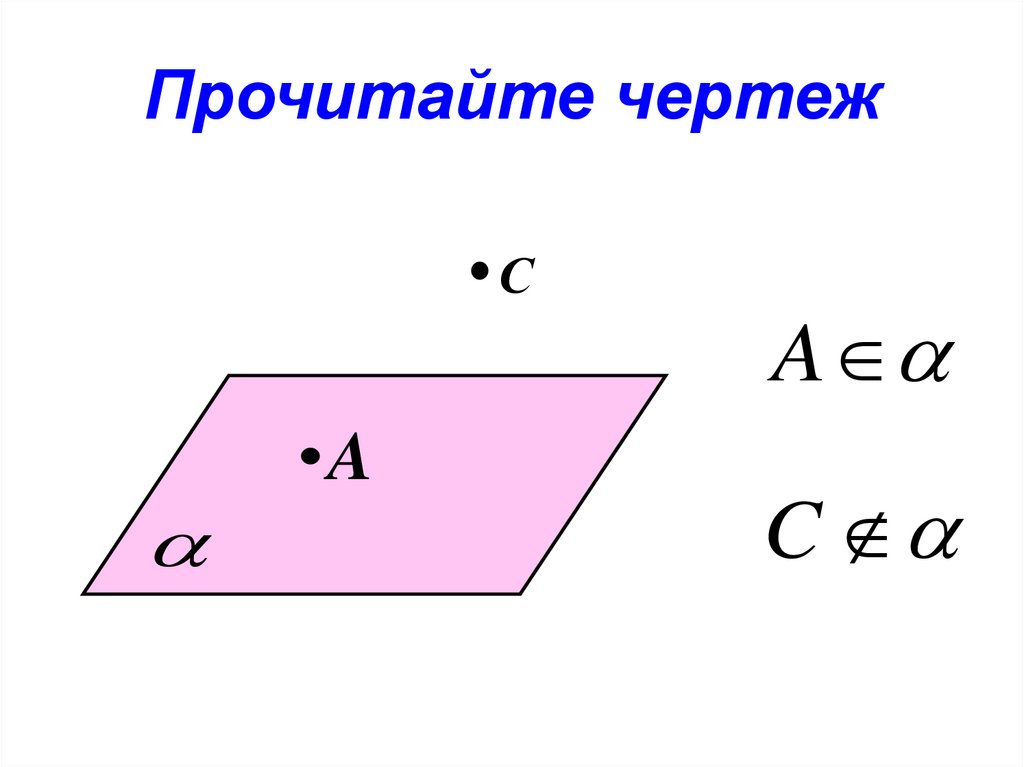
14. Прочитайте чертеж

С
A
A
C

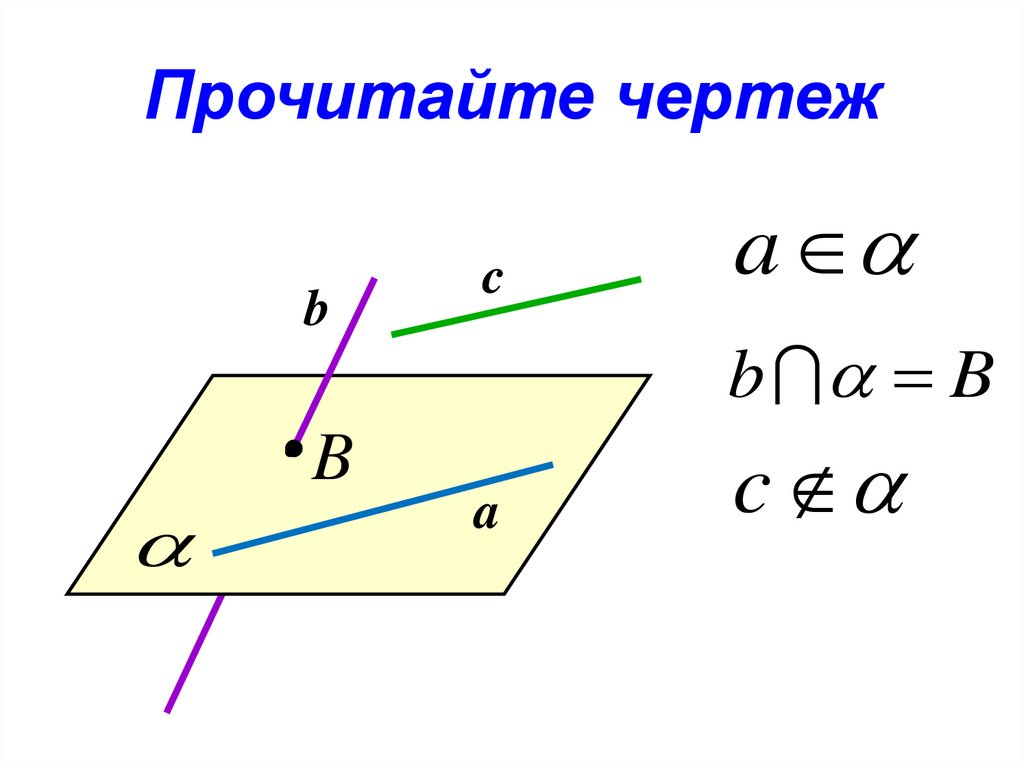
15. Прочитайте чертеж

b
B
c
a
b B
a
c

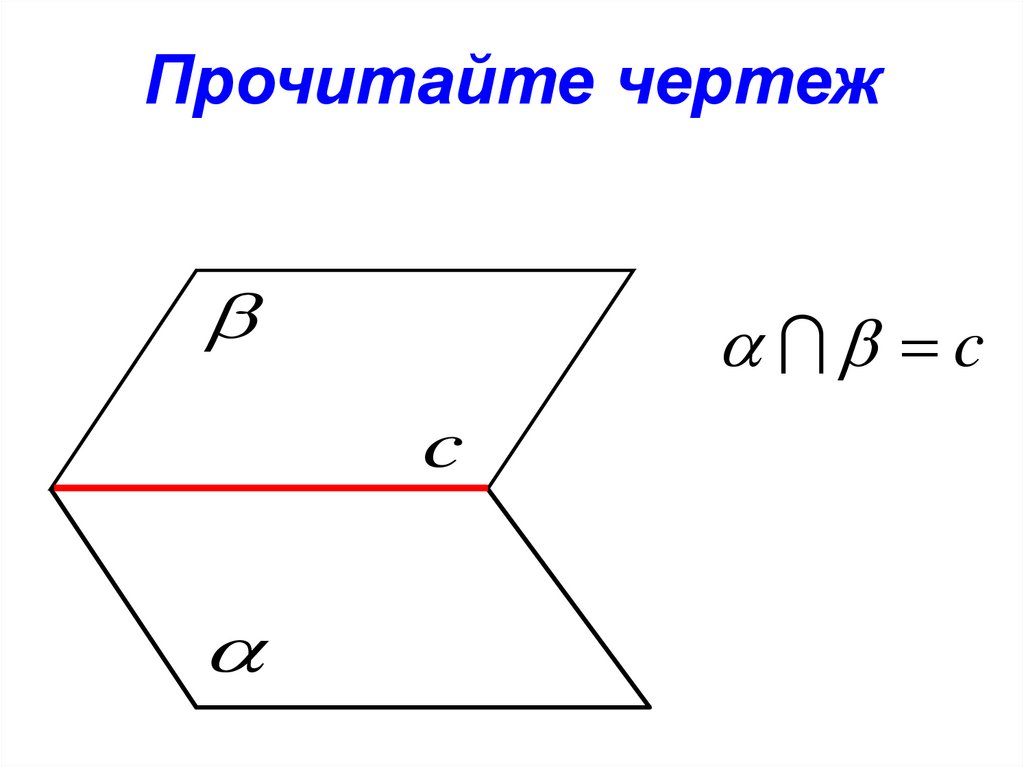
16. Прочитайте чертеж

c
c

17.

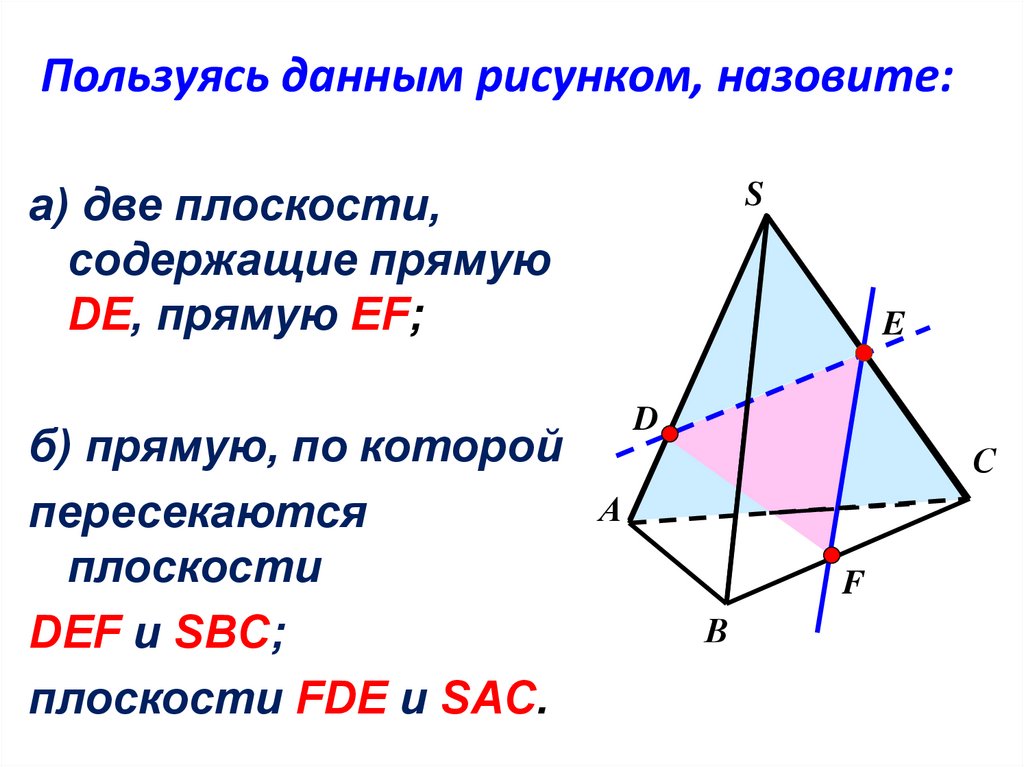
Пользуясь данным рисунком, назовите:
а) две плоскости,
содержащие прямую
DE, прямую EF;
б) прямую, по которой
пересекаются
плоскости
DEF и SBC;
плоскости FDE и SAC.
S
E
D
С
А
F
В

18. Домашнее задание:

1) Выучить аксиомы
2) Введение, п. 2,3,
стр. 4 – 6
3) № 1 (в, г); 2(в, г)