Похожие презентации:
Центральные и вписанные углы
1.
Корсакова А.В.,учитель математики
2.
Цели урокаповторить определения касательной, видов углов,
закрепить знания по теме, научить поиску
решения нестандартных задач;
активизировать
самостоятельность
и
познавательную
деятельность
обучающихся,
научить применять полученные знания на
практике.
3.
Теоретическая разминкадайте определение окружности.
что называется хордой
какой отрезок является радиусом окружности.
каково может быть взаимное расположение прямой и
окружности.
какая прямая называется касательной
сформулируйте свойство касательной
какой угол называется центральным
чему равна градусная мера дуги.
какой угол называется вписанным.
сформулируйте теорему о вписанном угле.
какие следствия из него знаете.
чему равен угол между касательной и хордой, проходящей через
точку касания.
сформулируйте теорему о двух пересекающихся хордах.
сформулируйте теорему о квадрате касательной.
4.
Тест «Верите ли вы, что…»Ответы:
1 вариант.
--+++---++2 вариант.
-++-++-+--+
5.
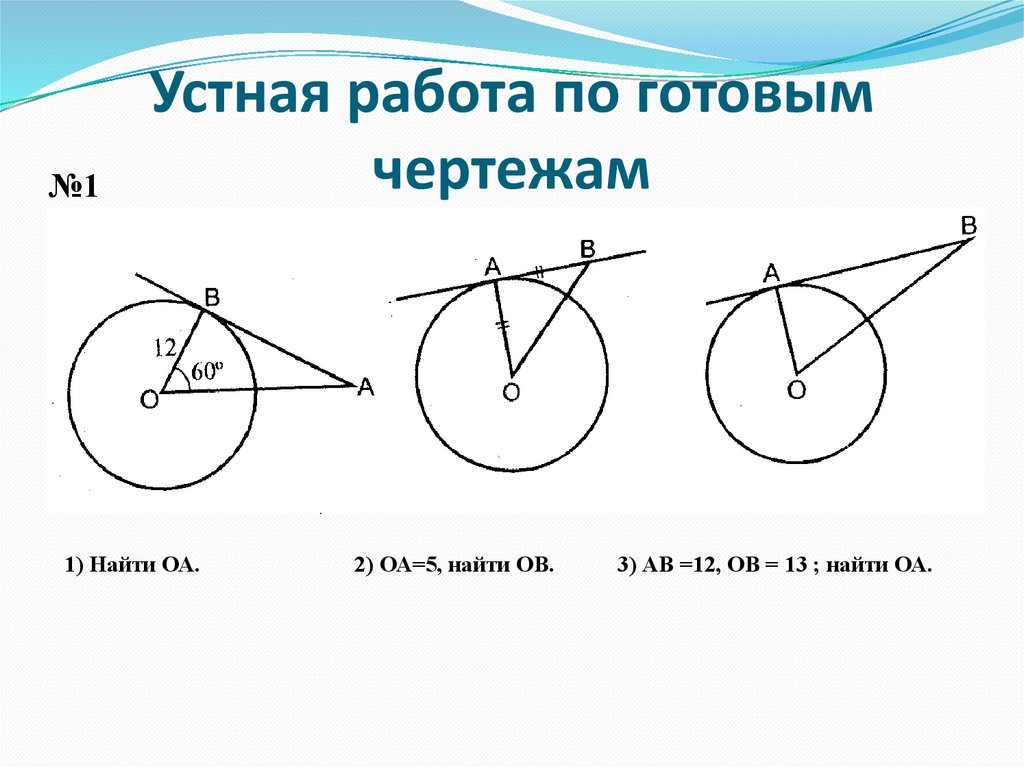
№1Устная работа по готовым
чертежам
1) Найти ОА.
2) ОА=5, найти ОВ.
3) АВ =12, ОВ = 13 ; найти ОА.
6.
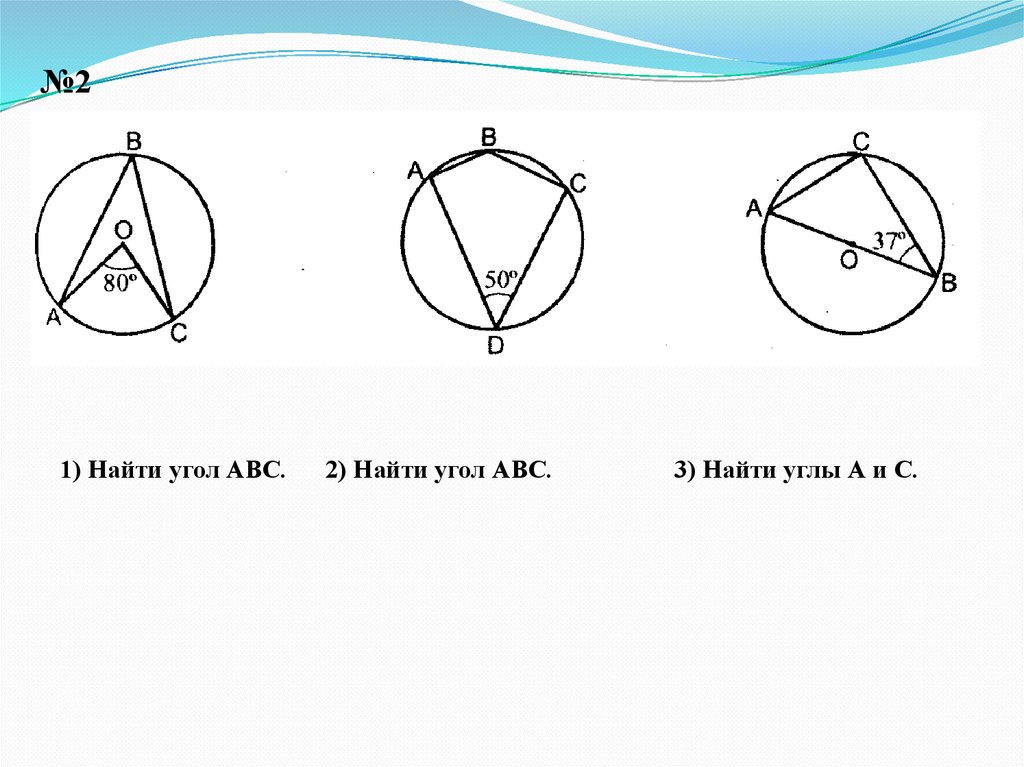
№21) Найти угол АВС.
2) Найти угол АВС.
3) Найти углы А и С.
7.
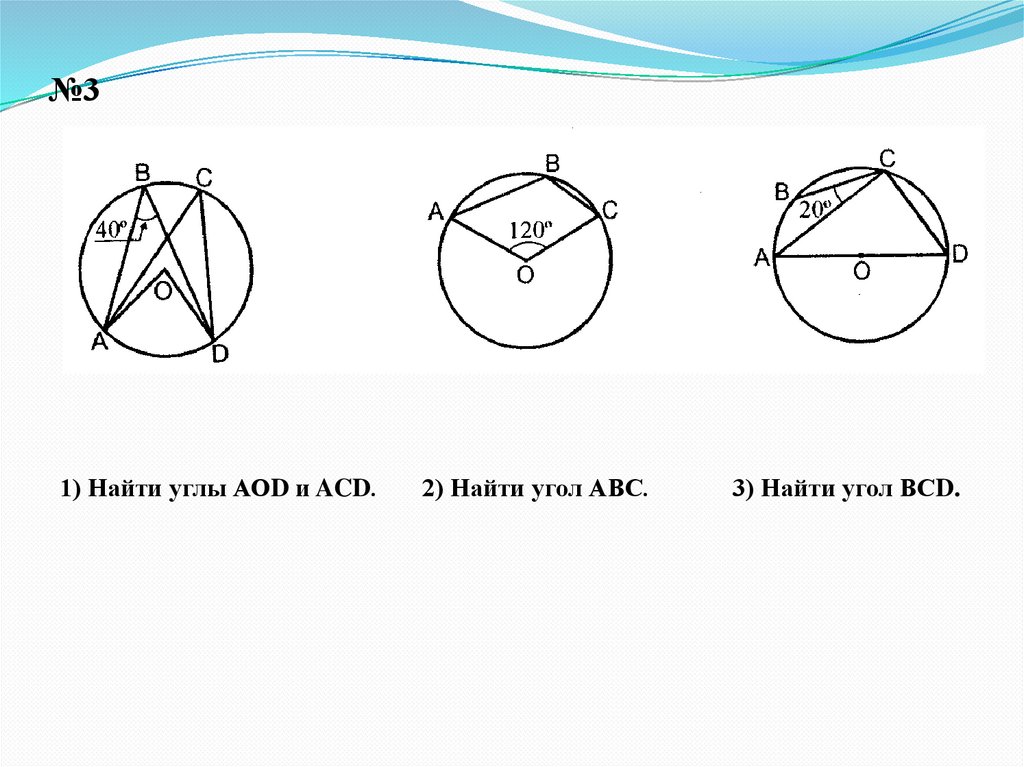
№31) Найти углы АОD и ACD.
2) Найти угол АВС.
3) Найти угол ВСD.
8.
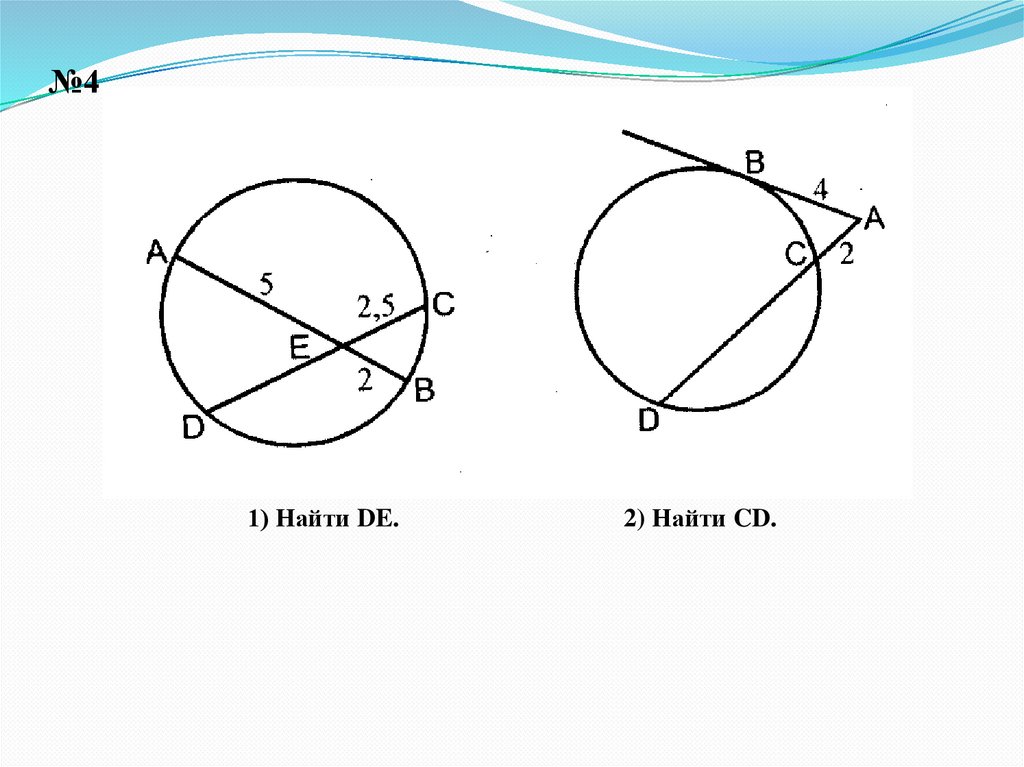
№41) Найти DE.
2) Найти CD.
9.
Задача:Найдите сумму углов пятиконечной звезды, вписанной в
окружность. (Рис. 1)
10.
Способы решения:I способ: Когда вершины пятиугольной звезды делят
окружность на равные дуги, задача решается очень
просто; 360о/5/2*5=180о.
II способ: Угол AMR – внешний угол треугольника
MCE, поэтому <AMR=<C+<E. Угол ARM – внешний
угол треугольника BRD, поэтому <ARM=<B+<D.
Тогда <A+<B+<C+<D+<E=<A+<AMR+<ARM=180o
11.
Формируемые УУДКоммуникативные
(умение строить речевое
высказывание в соответствии с поставленными
задачами)
Познавательные (умение находить ответы на
вопросы используя полученную информацию)
Регулятивные (разработка плана решения
задачи)







 Математика
Математика








