Оценка и обеспечение эксплуатационно-технических характеристик при проектировании подсистем автоматического управления (Часть 3)

1.

Тема 3. Оценка и
обеспечение
эксплуатационнотехнических характеристик
при проектировании
подсистем автоматического
управления
(Часть 3)
Дисциплина:
«АВТОМАТИКА В ЭЛЕКТРОННЫХ
СИСТЕМАХ БЕЗОПАСНОСТИ»

2.

Частотные характеристики
В условиях реальной эксплуатации САУ часто
возникает необходимость определить реакцию на
периодические сигналы, т.е. определить сигнал на
выходе САУ, если на один из входов подается
периодически сигнал гармонической формы. Решение
этой задачи возможно получить путем использования
частотных характеристик. Частотные характеристики
могут быть получены экспериментальным или
аналитическим путем. При аналитическом
определении исходным моментом является одна из
передаточных функций САУ (по управлению или по
возмущению.

3.

Если задана передаточная Функция W(S), то путём
подставки S=jω получаем частотную передаточную
функцию W(jω), которая является комплексным
выражением т.е. W(jω)=A(ω) + jK(ω),
где А(ω) вещественная составляющая, а К(ω) мнимая
составляющая. Частотными характеристиками
являются:
1) АФХ – амплитудно-фазовая частотная
характеристика

4.

2) ВЧХ – вещественная частотная характеристика;
3) МЧХ – мнимая частотная характеристика;
4) АЧХ – амплитудно-частотная характеристика
5) ФЧХ – фазовая частотная характеристика
6) Логарифмические частотные характеристики–
амплитудная и фазовая частотные характеристики в
логарифмических координатах.

5.

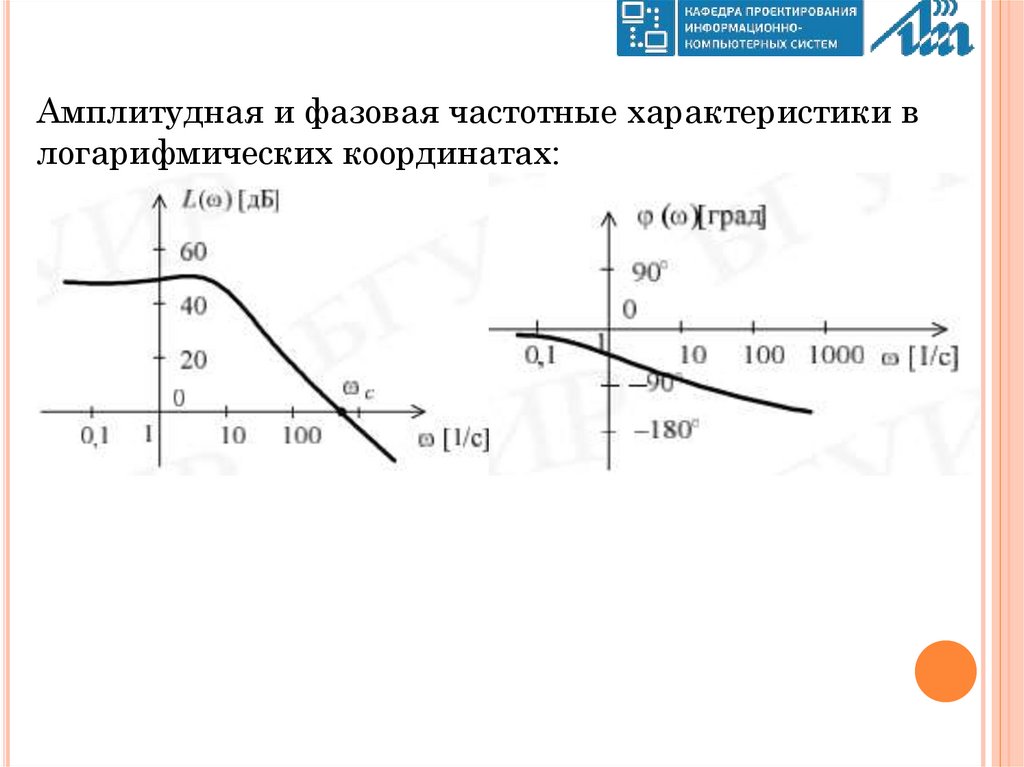
Амплитудная и фазовая частотные характеристики в
логарифмических координатах:

6.

Важными показателями качества системы являются
устойчивость и точность. Устойчивость определяется
как для линейных, так и нелинейных систем.
Линейная система называется устойчивой, если
при выведении ее внешними воздействиями из
состояния равновесия (покоя) она возвращается в него
после прекращения внешних воздействий. Если после
прекращения внешнего воздействия система не
возвращается к состоянию равновесия, то она является
неустойчивой. Для нормального функционирования
системы управления необходимо, чтобы она была
устойчивой, так как в противном случае в ней
возникают большие ошибки.

7.

Определение устойчивости обычно проводят на
начальном этапе создания системы управления. Это
объясняется двумя причинами. Во-первых, анализ
устойчивости довольно прост.
Во-вторых, неустойчивые системы могут быть
скорректированы, т.е. преобразованы в устойчивые с
помощью добавления специальных корректирующих
звеньев.
Оценка устойчивости систем определяется с помощью
различного рода критериев. Такими критериями
являются:

8.

1) Критерий Гурвица. Сущность критерия
заключается в составлении матрицы Гурвица. После
составления матрицы определяются все её
определители.

9.

По диагонали матрицы от верхнего левого угла
записываются по порядку все коэффициенты
уравнения начиная с а1. Затем каждый столбец
матрицы дополняется таким образом, чтобы вверх от
диагонали индексы коэффициентов увеличивались, а
вниз – уменьшались. Для устойчивой системы
необходимым и достаточным является то, чтобы при
а0>0 все диагональные определители были также
положительными, т.е.:
Система будет нейтральной в том случае, если Δn=0 и
все предыдущие определители положительны.

10.

2) Критерий Найквиста. Это частотный критерий,
позволяющий судить об устойчивости системы
замкнутой системы управления по АФЧХ разомкнутой.
Формулировка критерия следующая: если система
имеет l правых корней, то для того, чтобы замкнутая
система была устойчива, необходимо АФЧХ
разомкнутой системы W(jω) при изменениии частоты ω
от -∞ до +∞ охватывала точку (-1;j0) на комплексной
плоскости в положительном направлении l раз.
График для случая l=2:

11.

Основным назначением автоматической системы
является более точное воспроизведение управляющего
сигнала. Точность системы оценивается разностью
управляющего сигнала v(t) и выходом y(t), т.е.
величиной ошибки е(t)= v(t) - y(t). Очевидно чем
меньше величина ошибки, тем система точнее. На
практике пользуются понятием установившейся
ошибки ey(t).

12.

Существуют три вида ошибок:
1. Статическая ошибка ey0, которая определяется как: