Корневой критерий устойчивости. Лекция № 6

1.

Лекция № 6
1
Корневой критерий устойчивости
В теории автоматического управления разработаны специальные математические методы оценки
устойчивости, которые известны как критерии устойчивости. Они позволяют оценить влияние параметров
системы на устойчивость. Все критерии устойчивости делятся на: корневой; алгебраические и частотные.
Путем приравнивания знаменателя передаточной функции к нулю можно получить характеристическое
уравнение:
n
n 1
a0 s a1 s
... a n 0
Корни характеристического уравнения si могут быть как действительные, так и комплексные, и для
определения устойчивости откладываются на комплексной плоскости.
4
5
Im
3
6
1
0
Re
2
5
Корни si= j характеристического уравнения могут быть:
- действительные: положительные (корень № 1); отрицательные (2, 6);
нулевые (3);
- комплексные: комплексные сопряженные (4); чисто мнимые (5).
По кратности корни бывают одиночные (1, 2, 3) и сопряженные (4, 5).
4
Корневой критерий формулируется следующим образом:
Линейная АСР устойчива, если все корни характеристического уравнения лежат в левой
полуплоскости (имеют отрицательную вещественную часть). Если хотя бы один корень находится на
мнимой оси, которая является границей устойчивости, то говорят, что система находится на границе
устойчивости. Если хотя бы один корень находится в правой полуплоскости (не зависимо от числа корней в
левой), то система является неустойчивой.
Чтобы корни характеристического уравнения имели отрицательные вещественные части, необходимо чтобы
все его коэффициенты аi были положительны. Однако это условие является достаточным только для систем
описываемых ДУ 1-ого и 2-ого порядков. При n > 2 это условие недостаточно, если полином имеет комплексносопряженные корни.

2.

Алгебраический критерий устойчивости
2
Критерий Гурвица
Под алгебраическими критериями устойчивости понимают условия полученные из коэффициентов
характеристического уравнения, при выполнении которых линейная система устойчива, а при невыполнении неустойчива. Наибольшее распространение среди алгебраических критериев устойчивости получил критерий
Гурвица (швейцарский математик, 1885 г.).
Из коэффициентов характеристического уравнения: a0 s n + a1 s n-1 + ... + an-1 s + an = 0 , составляется
матрица главного определителя Δ:
a1 a 3 a 5 0
a0 a2 a4 0
Δ = 0 a1 a 3 0
0 0 0 an
По диагонали матрицы от верхнего левого угла записываются по порядку все
коэффициенты характеристического уравнения, начиная с а1. Затем каждый столбец
матрицы дополняется таким образом, чтобы вверх от диагонали индексы
коэффициентов увеличивались, а вниз уменьшались.
Определение критерия:
Для устойчивой системы необходимым и достаточным условием является то, чтобы главный
определитель Δ и все n диагональные миноры Δn получаемые из квадратной матрицы коэффициентов
должны быть положительны, при a0 > 0.
Матрицы, для расчета диагональных миноров Δn, получают из исходной Δ путем последовательного
исключения последних столбца и строки:
1 a 1 0;
2
a1
a0
a3
0
a2
и т.д.
Если хотя бы один определитель будет равен нулю, то система будет находится на границе устойчивости.
Если хотя бы один определитель будет отрицателен, то система неустойчива, не зависимо от числа
положительных или нулевых определителей.
К алгебраическим критерия относят также критерии Рауса (1877г.), Льенара—Шипара (1914г.) и др.

3.

Критерий Рауса
3
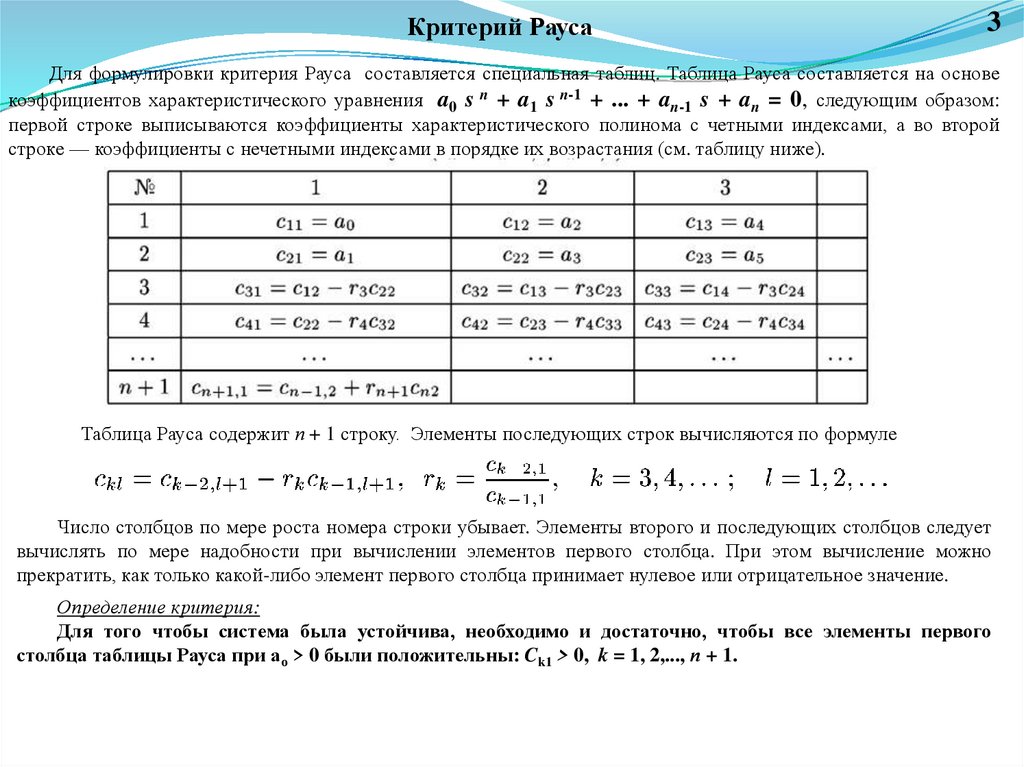
Для формулировки критерия Рауса составляется специальная таблиц. Таблица Рауса составляется на основе
коэффициентов характеристического уравнения a0 s n + a1 s n-1 + ... + an-1 s + an = 0, следующим образом:
первой строке выписываются коэффициенты характеристического полинома с четными индексами, а во второй
строке — коэффициенты с нечетными индексами в порядке их возрастания (см. таблицу ниже).
Таблица Рауса содержит п + 1 строку. Элементы последующих строк вычисляются по формуле
Число столбцов по мере роста номера строки убывает. Элементы второго и последующих столбцов следует
вычислять по мере надобности при вычислении элементов первого столбца. При этом вычисление можно
прекратить, как только какой-либо элемент первого столбца принимает нулевое или отрицательное значение.
Определение критерия:
Для того чтобы система была устойчива, необходимо и достаточно, чтобы все элементы первого
столбца таблицы Рауса при ао > 0 были положительны: Ck1 > 0, k = 1, 2,..., п + 1.

4.

Частотные критерии устойчивости
4
Принцип аргумента
Запишем характеристическое уравнение в форме Безу: an(p-p1)… (p-pn)=0, где pi - корни уравнения, в
общем случае комплексные: pi=αi+jβi , p - некоторая переменная величина.
Если заменить в левой части уравнения p → jω, то получим функцию:
D(jω)=an(jω-p1)… (jω-pn)
Каждая скобка на комплексной плоскости изобразится в
виде вектора, причем, все вектора pi начинаются в начале
координат, а заканчиваются в правой полуплоскости при
положительных действительных частях, или в левой –
при отрицательных (см. рисунок).
Если частота ω изменяется от – ∞ до +∞ то вектор разности будет поворачиваться на угол π по часовой стрелке
при α > 0 или против часовой стрелки, если α < 0. Поскольку D(jω) можно представить как D(jω)=A(ω)ejγ(ω)
где
,
, то получается что фазовый угол
равен сумме фазовых углов всех составляющих скобок.
При изменении ω от - ∞ до +∞ вектор D(jω) повернется на угол: g=(n-m)π-mπ, где n- общее число
корней, m – число правых корней, а поворот против часовой стрелки считается положительным.
При изменении ω от 0 до +∞ вектор D(jω) повернется на угол: g=(n-2m)(π/2)
Отсюда вытекает правило: изменение аргумента вектора p при изменении частоты ω от - ∞ до +∞
равно разности между числом левых и правых корней уравнения D(jω) = 0 умноженному на π, а при
изменении частоты от 0 до + эта разность умножается на π/2.
Это и есть принцип аргумента. Он положен в основе всех частотных критериев устойчивости. Рассмотрим
далее два наиболее распространенных критерия: критерий Михайлова и критерий Найквиста.

5.

Критерий Михайлова
5
Критерий А. В. Михайлова (советский учёный, 1938г.) предполагает построение годографа (АФЧХ) на
комплексной плоскости. Для построения годографа, из характеристического уравнения путем подстановки
вместо s j получают аналитическое выражение вектора D(j ):
D( j ) a0 ( j ) n a1 ( j ) n 1 ... an
Данное уравнение является комплексным и может быть представлено в виде: D j Re( ) j Im( )
На комплексной плоскости, изменяя частоту от 0 до строится по Re( ) и Im( ) годограф Михайлова D(j ).
Определение критерия Михайлова:
Для устойчивой АСР необходимо и достаточно,
чтобы годограф Михайлова (см. рисунок), начинаясь
при = 0 на положительной вещественной полуоси,
обходил
последовательно
в
положительном
направлении (против часовой стрелки) при
возрастании от 0 до n квадрантов, где n - степень
характеристического полинома.
Если годограф Михайлова проходит через начало
координат, то говорят, что система находится на границе
устойчивости.
Если годограф пройдет через начало координат – уравнение имеет чисто мнимые корни.
Если он начнется в начале координат – уравнение имеет нулевые корни.
Если нарушит порядок обхода четвертей или не пройдет n четвертей – уравнение содержит правые корни.

6.

6
Критерий Найквиста
Частотный критерий Х. Найквиста (американский инженер, 1932г.) разработан для анализа устойчивости
динамических систем, имеющих обратные связи (замкнутые). Критерий аналогичен критерию Михайлова и
позволяет по АФЧХ разомкнутой системы судить об устойчивости замкнутой системы, полученной охватом
разомкнутой системы единичной отрицательной обратной связью.
Порядок применения критерия Найквиста:
1) Определяется передаточная функция разомкнутой системы.
2) Определяется число правых корней m характеристического уравнения разомкнутой системы.
3) Определяется частотная передаточная функция подстановкой s = j : Wрс(j ) = Re( ) + Im( ).
4) На комплексной плоскости строится по Re( ) и Im( ) (изменяя частоту от 0 до ) АФЧХ разомкнутой
системы.
Определение критерия:
Чтобы
система
в
замкнутом
состоянии была устойчивой необходимо и
достаточно, чтобы при изменении ω от -∞
до +∞ годограф разомкнутой системы
Wрс(jw) (АФЧХ), поворачиваясь вокруг
начала координат по часовой стрелке,
охватил точку (-1, j0) m/2 раз, где m - число
правых корней разомкнутой системы.
Если АФХ проходит через точку (-1; j0), то замкнутая система находится на границе устойчивости (график 3).

7.

7
В случае, когда характеристическое уравнение разомкнутой системы не имеет правых корней (т. е. m = 0),
то согласно критерию Найквиста, замкнутая система является устойчивой, если АФЧХ разомкнутой
системы Wрс(j ) не охватывает точку (-1; j0), в противном случае система будет неустойчива.
Im
Уст.
Оценка устойчивости по критерию
Найквиста (для m=0)
-1
0
Re
Неуст.
В случае если разомкнутая система астатическая и ее характеристическое уравнение не имеет правых
корней, но имеет k нулевых, замкнутая система будет устойчивой, если АФЧХ разомкнутой системы,
дополненная дугой окружности с центром в начале координат, радиусом больше единицы, начинающейся на
положительной действительной полуоси и проходящей по часовой стрелке k четвертей до пересечения с
АФЧХ, не охватывает точку с координатами (-1; j0).

8.

Определение устойчивости по
логарифмическим частотным характеристикам
8
Если АФЧХ охватывает точку (-1, j0), то она пересекает отрезок (-∞,-1) вещественной оси. Точку
пересечения АФЧХ с указанным отрезком называют положительным переходом, если пересечение происходит
при возрастании частоты сверху вниз (т.е. в положительном направлении), и отрицательным переходом, если
пересечение происходит снизу вверх (рис. а). Если АФЧХ начинается или кончается на отрезке (-∞, - 1), то
говорят о 1/2-переходе (рис. а).
Определение критерия Найквиста для ЛЧХ :
Для того чтобы замкнутая система
управления была устойчива, необходимо и
достаточно,
чтобы
разность
между
положительными и отрицательными переходами
была равна m/2 (m - число правых корней
характеристического уравнения разомкнутой
системы).
стема
находится
на
границе
устойчивости
При пересечении АФЧХ отрезка (-∞, - 1) (рис. б) амплитудная частотная функция А(ω) > 1 и соответственно
L(ω) > 0, фазовая частотная функция φ(ω) = ±(2k + 1)π (k = 0,1, 2...). Поэтому на логарифмических частотных
характеристиках (ЛЧХ) положительным переходам соответствуют точки пересечения логарифмической фазовой
частотной характеристики (ЛФЧХ) прямой φ(ω) = ±(2k + 1) (k = 0,1, 2...) снизу вверх (в сторону возрастания φ(ω)),
отрицательным переходам - сверху вниз при частотах, когда L(ω) > 0 (рис. б).
На основании критерия Найквиста получаем логарифмический частотный критерий устойчивости:
Для того чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы разность между
положительными и отрицательными переходами ЛФЧХ прямой φ(ω) = ±(2k + 1)π (k = 0,1, 2...) при
частотах, когда L(ω) > 0 (логарифмическая амплитудная частотная характеристика положительна), была
равна m/2 (m - число правых корней характеристического уравнения разомкнутой системы).

9.

Определение области устойчивости
9
Метод D-разбиения
Областью устойчивости в пространстве параметров называют множество всех значений варьируемых
параметров, при которых система устойчива.
Если существует область устойчивости в пространстве параметров, т. е. существуют такие значения
варьируемых параметров, при которых система устойчива, то она называется структурно устойчивой или
структурно устойчивой относительно заданных варьируемых параметров.
Область устойчивости можно определить с помощью алгебраических критериев устойчивости. Одним из
таких методов определения области устойчивости является методом D-разбиения.
Если имеются варьируемые параметры, то корни характеристического уравнения зависят от этих параметров,
и пространство параметров можно разбить на области, которым соответствует фиксированное количество левых
корней. Область, которой соответствует k левых корней характеристического уравнения, обозначим D(k). В общем
случае все пространство параметров можно разбить на области D(0), D(1), … D(n). Область D(n) является
областью устойчивости, так как при значениях параметров из этой области п корней являются левыми.
Разбиение пространства параметров на все возможные области D(k) называется D-разбиением. Кривая,
разделяющая области D(k) с различными индексами k, называется кривой D-разбиения.
Применение метода D-разбиения (Ю.И. Неймарк советский и российский математик, 1948 г.) включает
следующие три операции:
1) D-разбиение пространства параметров;
2) определение среди областей D(k) области, имеющей наибольший индекс. Эта область называется областью
- претендентом, так как только эта область может быть областью устойчивости;
3) проверка, является ли область-претендент областью устойчивости. Для этого фиксируется какая-либо точка
внутри области-претендента и при значении варьируемых параметров, соответствующих фиксированной точке,
проверяется устойчивость системы. Если система устойчива, область-претендент является областью устойчивости.

10.

10
Для получения уравнения кривой D-разбиения делается подстановка s → jω в характеристическое
уравнение и выделяется действительная μ и мнимая части jμ́.
Для построения кривой D-разбиения вместо изменения ω от -∞ до +∞, достаточно построить кривую Dразбиения при изменении ω от 0 до ∞, а затем для получения участка кривой, соответствующего
отрицательным ω, зеркально отобразить ее относительно вещественной оси. Для выделения областипретендента кривую D-разбиения штрихуют слева при движении по ней в сторону возрастания ω .
При пересечении кривой со штрихованной
стороны на не штрихованную один левый корень
становится правым, а при пересечении с обратной
стороны один правый корень становится левым.
Поэтому если, например, область 1 принять за
область D(r), то область 2 будет областью D(r + 1) и
область 3 - областью D(r - 1).
Следовательно, областью-претендентом на
устойчивость будет область 2.
Выделение области устойчивости на плоскости
одного параметра

11.

Робастная устойчивость
11
Параметры стационарных систем с течением времени в силу старения или других причин могут меняться.
Кроме того, при разработке регуляторов параметры объекта могут быть точно не известны. В подобных случаях
возникает необходимость построения системы управления таким образом, чтобы она была устойчива не при
одних фиксированных значениях параметров, а при всех возможных их значениях и обеспечивала приемлемое
качество управления при малых отклонениях внешних возмущений от номинальных значений. В современной
теории управления это свойство называют робастностью (грубостью).
Рассмотрим характеристический полином
Δ(s)=a0 s n + a1 s n-1 + ... + an-1 s + an .
Полином Δ(s) называется робастно устойчивым, если он является устойчивым при любых значениях
коэффициентов ai , (i = 0,1,..., n) из множества допустимых значений A ( ai А ).
Система называется робастно устойчивой или робастно устойчивой на множестве А, если ее
характеристический полином является робастно устойчивым полиномом в А.
Для исследования робастной устойчивости систем управления на практике используется подход,
базирующийся на теореме Харитонова, которая позволяет проверить робастную устойчивость
характеристического полинома:
Δ(s)=a0 s n + a1 s n-1 + ... + an-1 s + an.,
где коэффициенты a0, a1,..., a, точно неизвестны, но принадлежат определенным интервалам ai ai ai ,( i 1,...,n ,)
где a i , ai - минимальное и максимальное значения коэффициентов ai , (i 1,..., n).

12.

11
Теорема В.Л. Харитонова (1978 г.)
Для того чтобы система с характеристическим полиномом
Δ(s)=a0 s n + a1 s n-1 + ... + an
была робастно устойчива в параллелепипеде А, необходимо и достаточно, чтобы все полиномы Харитонова были
устойчивыми.
Множество А здесь является параллелепипедом А ai : ai ai ai ,( i 1,...,n ) .
Для проверки устойчивости бесконечного числа возможных характеристических полиномов Δ(s) при всех
возможных значениях коэффициентов ai А , достаточно проверить устойчивость всего четырех полиномов
Харитонова (например, для n=6):
1 ( s) a 0 s 6 a 1 s 5 a 2 s 4 a 3 s 3 a 4 s 2 a 5 s a 6 ;
2 ( s) a 0 s 6 a1 s 5 a 2 s 4 a 3 s 3 a 4 s 2 a 5 s a 6 ;
3 ( s) a 0 s 6 a1 s 5 a 2 s 4 a 3 s 3 a 4 s 2 a 5 s a 6 ;
4 ( s ) a 0 s 6 a 1 s 5 a 2 s 4 a 3 s 3 a 4 s 2 a 5 s a 6 .
Следствие.
Для того чтобы система с характеристическим полиномом Δ(s)=a0 s n + a1 s n-1 + ... + an.была робастно
устойчива в параллелепипеде при выполнении условия , необходимо и достаточно, чтобы были устойчивыми:
а) в случае n = 3 полином Харитонова Δ1(s) ;
б) в случае n = 4 полиномы Харитонова Δ1(s) , Δ2(s) ;
в) в случае n = 5 полиномы Харитонова Δ1(s) , Δ2(s) , Δ3(s).

13.

Вопросы для самоконтроля
13
1. Как формулируется корневой критерий устойчивости?
2. Как определяется устойчивость по критерию Гурвица?
3. Как определяется устойчивость по критерию Михайлова?
4. Как определяется устойчивость по критерию Найквиста?
5. Как можно определить устойчивость САУ по логарифмическим частотным характеристикам?
6. Что такое запас устойчивости по амплитуде и по фазе?
7. Что такое область устойчивости?
8. В чем суть метода D-разбиения?
9. Что такое «робастная устойчивость»?
10. Как формулируется теорема Харитонова для оценки робастной устойчивости?