Краткий теоретический справочник

1.

Содержание
справочника

2.

Глава I. Краткий теоретический справочник.
§1. Определение квадратного уравнения.
§2.
§3.
§4.
§5.
§6.
§7.
Неполные квадратные уравнения.
Формула корней квадратного уравнения.
Формула корней квадратного уравнения с чётным вторым коэффициентом.
Приёмы устного решения квадратных уравнений.
Теорема Виета.
Биквадратные уравнения.
Глава II. Алгоритмы решения типовых задач.
Глава III. Учебно-тренировочные задания.
Глава IV. По страницам истории.
Содержание
справочника
Завершение
работы

3.

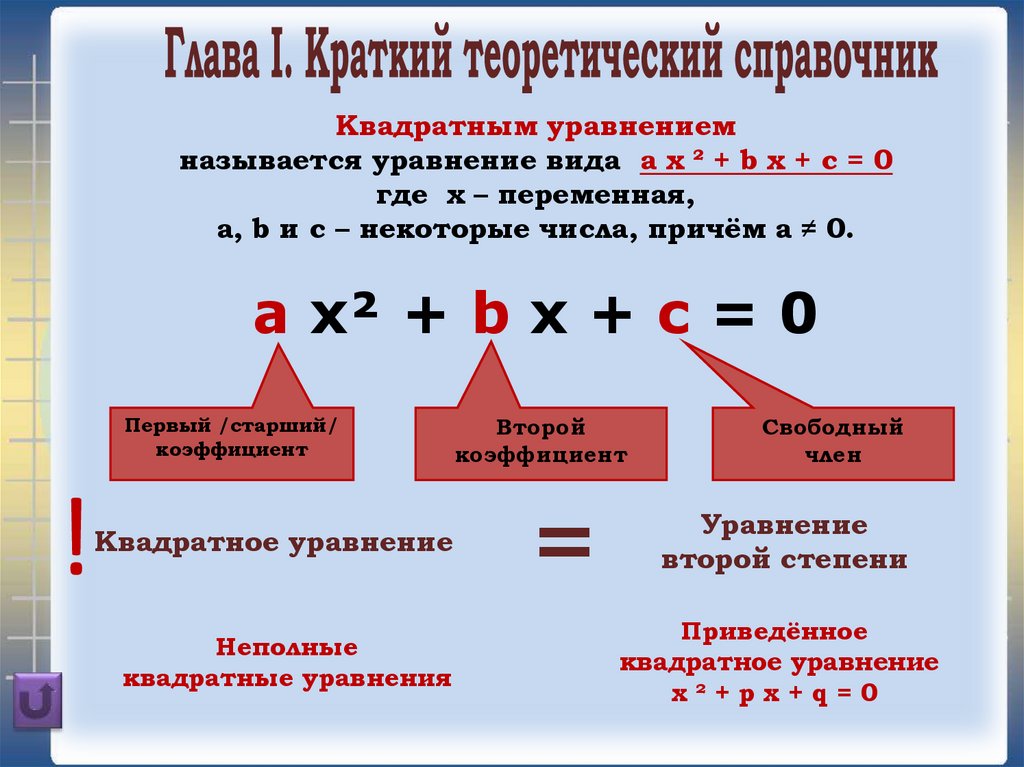
Квадратным уравнением
называется уравнение вида a x ² + b x + c = 0
где х – переменная,
a, b и c – некоторые числа, причём а ≠ 0.
a x² + b x + c = 0
Первый /старший/
коэффициент
!
Квадратное уравнение
Неполные
квадратные уравнения
Второй
коэффициент
=
Свободный
член
Уравнение
второй степени
Приведённое
квадратное уравнение
x²+px+q=0

4.

Неполные квадратные уравнения
хотя бы один из коэффициентов b или с равен нулю
ax² +c = 0, b=0
ax² = -c,
x² = -
ax² +bx = 0, с=0
x(ах + b) = 0,
x = 0 или ax+b = 0,
ax=-b,
x= -
Пример:
3x ² -27 = 0,
3x² = 27,
x ² = 9,
х=-3 или х=3.
Ответ: -3; 3.
ax² = 0, b=0 и с=0
x² = 0 : а,
x² = 0,
х=0.
.
Пример:
2x ² +7х = 0,
х (2х +7) = 0,
х = 0 или 2х +7 = 0,
2х = -7,
х = -3,5.
Ответ: 0; -3,5.
Пример:
3x ² = 0,
x² = 0:3,
x ² = 0,
х=0 .
Ответ: 0.

5.

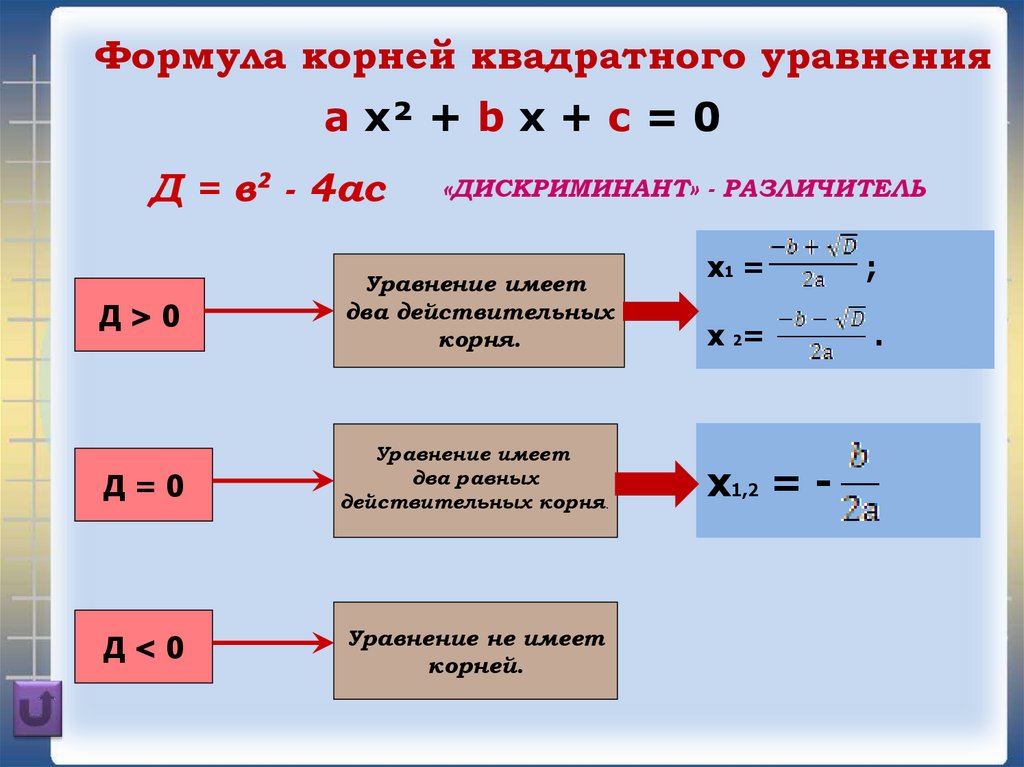
Формула корней квадратного уравнения
a x² + b x + c = 0
Д = в² - 4ас
«ДИСКРИМИНАНТ» - РАЗЛИЧИТЕЛЬ
Д>0
Уравнение имеет
два действительных
корня.
Д=0
Уравнение имеет
два равных
действительных корня.
Д<0
Уравнение не имеет
корней.
х1 =
;
х 2=
.
х1,2 = -

6.

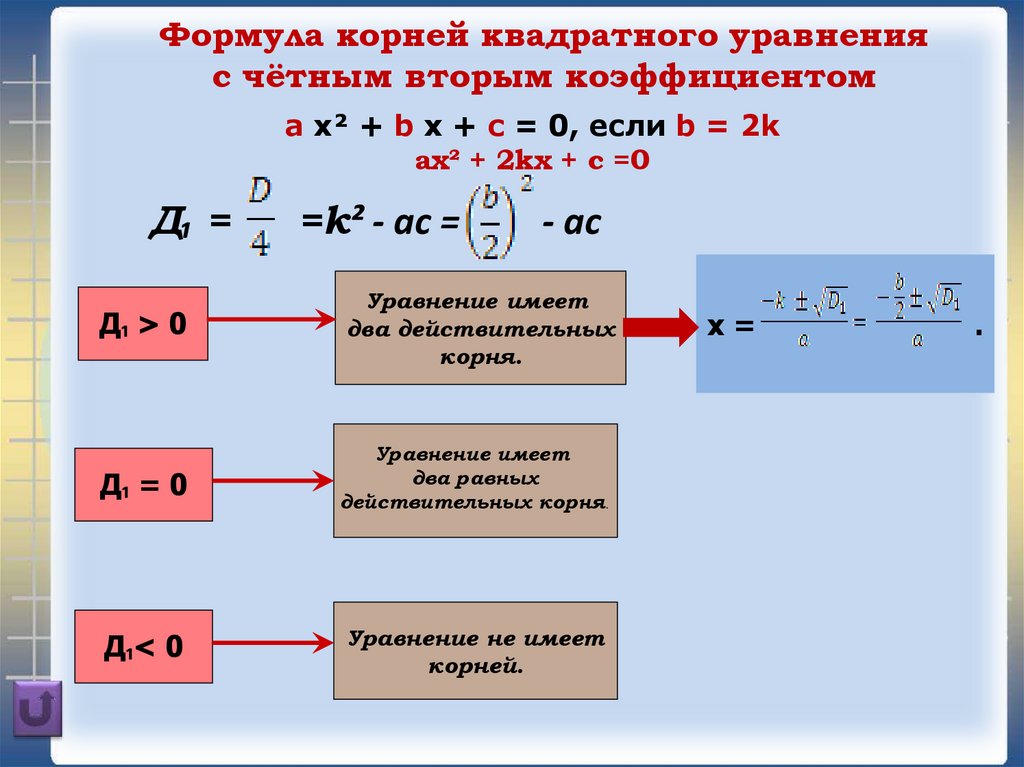
Формула корней квадратного уравнения
с чётным вторым коэффициентом
a x² + b x + c = 0, если b = 2k
ax² + 2kx + c =0
Д₁ =
=k² - ac =
- ac
Д₁ > 0
Уравнение имеет
два действительных
корня.
Д₁ = 0
Уравнение имеет
два равных
действительных корня.
Д₁< 0
Уравнение не имеет
корней.
х=
.

7.

Приёмы устного решения
квадратных уравнений.
a x ² + b x + c = 0.
Основа:
Рассмотрим функцию f (x) = a x ² + b x + c ;
f (1) = a + b + c;
f (- 1) = a - b + c.
1.Если a + b + c = 0, то один корень уравнения x = 1, а
второй x =
.
2.Если a - b + c = 0, то один корень уравнения x = - 1, а
второй x = 3. Если a = c, b = a² + 1, то один корень уравнения
x = - a, а второй x = - .
4. Если a = c, b = -(a² + 1), то один корень уравнения x = a, а
второй x = .

8.

Приведённое квадратное уравнение
x² + px + q =0
Старший коэффициент равен 1
Теорема Виета
Если х₁ и х₂ корни приведённого квадратного
уравнения
х² + px + q = 0 ,
то x₁ + x₂ = - p,
а
x₁ ∙x₂ = q.
Обратное утверждение:
Если числа m и n таковы, что m + n = - p, mn = q, то эти
числа являются корнями уравнения х² + px + q = 0.
Обобщённая теорема:
Числа
х₁
и х₂
являются корнями приведённого квадратного
уравнения х² + px + q = 0 тогда и только тогда, когда
x₁ + x₂ = - p,
x₁∙ x₂ = q.
Следствие: Формула разложения квадратного трёхчлена на
множители: ах² + bx + c = a(х – х₁)(х – х₂)

9.

Биквадратное уравнение
a x⁴ + b x² + c = 0
а≠0, b и c –заданные числа
Заменой х² =t – сводится к квадратному уравнению.
9х⁴ +17х² -2 = 0,
Пусть х² = t, тогда 9t² +17t – 2 =0,
t = -2 или t =
,
Значит х² = -2 или х² =
Нет корней
Ответ: -
х₁ = , х₂ = , .

10.

Уровень А
Задача 1. Решите уравнение:
а) 10х² + 5х = 0,
5х(2х +1)=0,
5х=0 или 2х+1=0,
х=0
2х= -1,
х= -0,5.
Ответ: -0,5; 0.
б) 25 - 100х² = 0,
I сп: -100х² = -25,
х² = 0,25,
х₁ = - 0,5 или х₂= 0,5.
Ответ: -0,5; 0,5.
II сп: (5-10х)(5+10х)=0,
5-10х=0 или 5+10х =0,
-10х = -5
10х =-5,
х= 0,5
х= -0,5,
Ответ: -0,5; 0,5.

11.

Уровень А
Задача 2. Решите уравнение:
а) 2х² - 7х +5 = 0,
D = b² - 4ac = (-7)²- 4∙2∙5 = 49-40 =9>0, 2 корня;
х₁ =
=
= 2,5,
х₂ =
=
=3.
=1.
Ответ: 1; 2,5.
а) 4х² - 8х - 5 = 0,
а=4, b =-8, с= -5, k = -4
D₁ = k² - ac = (-4)²- 4∙(-5 )= 16 + 20 =36 >0, 2 корня;
=6.
х₁ =
=
Ответ: -0,5; 2,5.
= -0,5;
х₂ =
=
=2,5.

12.

Ситуации, в которых может
использоваться теорема Виета.
Проверка правильности найденных корней.
Определение знаков корней квадратного
уравнения.
Устное нахождение целых корней приведённого
квадратного уравнения.
Составление квадратных уравнений с
заданными корнями.
Разложение квадратного трёхчлена на
множители.

13.

Уровень А
Задача 5. Решите уравнение:
(у + 1) ∙ у = 12.
Решение:
(у +1)· у =12,
у² + у -12 = 0,
По теореме , обратной теореме Виета:
у₁ + у₂ = -1,
у₁ ∙ у₂ = -12
у₁ = -4, у₂ = 3.
Ответ: -4 ; 3.

14.

Уровень А
Задача 4. Какое выражение надо подставить вместо
многоточия, чтобы было верным равенство:
2х² +5х -3 = 2(х+3) (…)?
Решение: Воспользуемся формулой разложения квадратного
трёхчлена на множители.
ах² + bx + c = a(х – х₁)(х – х₂)
2х² +5х -3 = 2 (х - ) (х – )
2х² +5х -3 = 2 (х +3) (х – 0,5)
2х² + 5х -3 =0,
D = 5² - 4∙ 2 ∙ (-3) = 25 + 24 = 49>0, 2 корня
х₁ =
= -3, х₂ =
= 0,5
Ответ: х -0,5.

15.

Уровень В
Задача 5. Решите уравнение:
х⁴ + 2х² -8 = 0.
Решение:
Пусть х² =t,
t² +2t -8 = 0,
D₁ = k² - ac = 1-1∙ (-8) = 9 >0, 2 корня.
t₁ =
x² = -4 ,
корней нет
Ответ: ,
= -4,
t₂ =
=3
= 2.
х² =2
х₁ =
,
х₂ = -
.

16.

Дорогой друг!
Тебе предоставляется возможность проверить
свои знания по теме «Квадратные уравнения».
Данная работа состоит из 5 заданий уровня А
и 5 заданий уровня В.
Уровень А
Вернуться к
содержанию
Уровень В
Завершение
работы

17.

Уровень А
№1. Решите уравнение:
а) 64 – 25 х² =0;
б) х² - х – 6 = 0;
в) х ( х + 6) = 2х -3;
г) 2у (у - 3) = -9;
№2. Соотнесите квадратные уравнения и их корни:
1) х² + 5х – 6 =0
А) х₁ = 1, х₂ = -6
2) х² -6х +9 =0
Б) х₁ = 0, х₂ = 2
3) х(х - 2) = 0
В) х = 3.
Проверь себя!
Проверь себя!
№3. Укажите отрицательный корень уравнения
Проверь себя!
5х² + 7 (х - 2) = 4х² - 14.
№4. Какое выражение надо подставить вместо
многоточия, чтобы было верным равенство: 3
Проверь себя!
3х² + 5х – 2 = 3 (х + 2) (…)?
№5. Сумма
и произведение корней некоторого
квадратного уравнения равны соответственно
2 и -3.
Определите это уравнение.
Проверь себя!
А. х² + 5х -6 =0
Б. Х² - 5х – 6= 0
В. х² + 2х – 3 = 0 Г. х² - 2х – 3 = 0.

18.

Уровень В
№1. Решите уравнение:
х³ + 3х² - 4х – 12 = 0.
Проверь себя!
№2. Решите уравнение:
х⁴ - 7х² +12 = 0.
Проверь себя!
№3. Выясните, имеет ли корни уравнение:
х + √х - 20 =0 .
Проверь себя!
№4. Решите уравнение:
(х² + 4х)(х² + 4х - 17) = -60.
№5. Решите уравнение:
(х² - 7х +13)² – (х - 3) (х - 4) = 1.
Проверь себя!
Проверь себя!

19.

Проверь себя!
№1. Ответы:
а) х₁ = - 1,6;
х₂ = 1,6
б) х₁ = - 2;
х₂ = 3.
в) х₁ = - 3;
х₂ = -1.
г) корней нет.
Уровень А

20.

Проверь себя!
Уровень А
№2. Ответ:
1
2
3
А
В
Б

21.

Проверь себя!
№3. Ответ:
х = -7.
Уровень А

22.

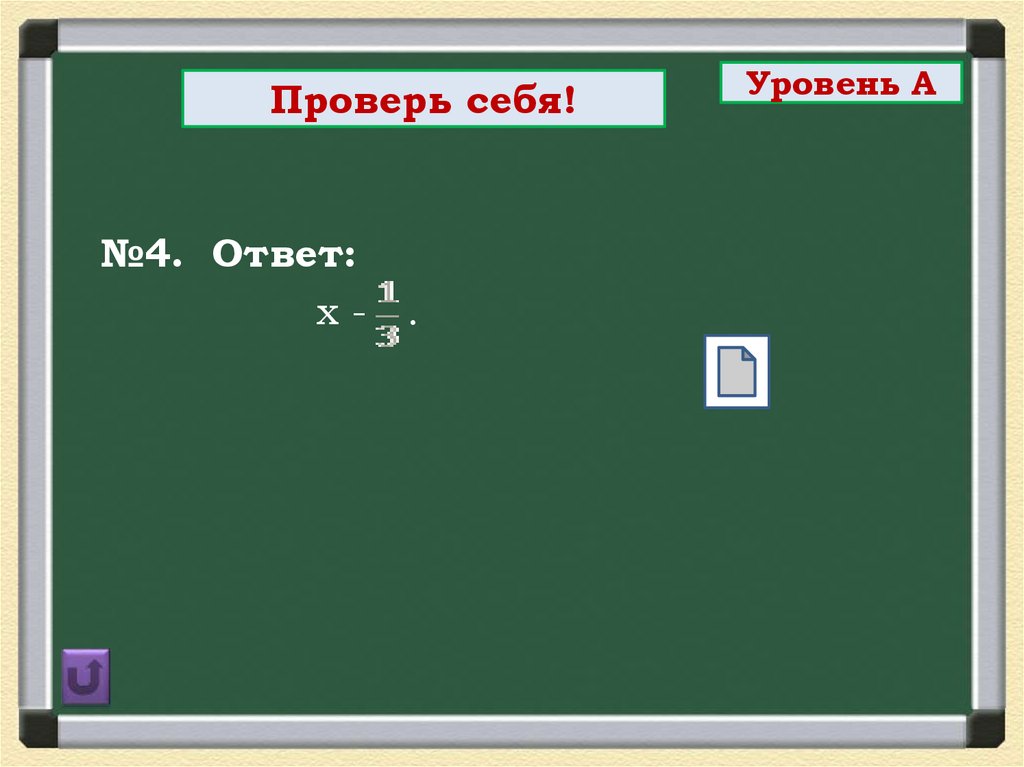
Проверь себя!
№4. Ответ:
х- .
Уровень А

23.

Проверь себя!
№5. Ответ: Г
Уровень А

24.

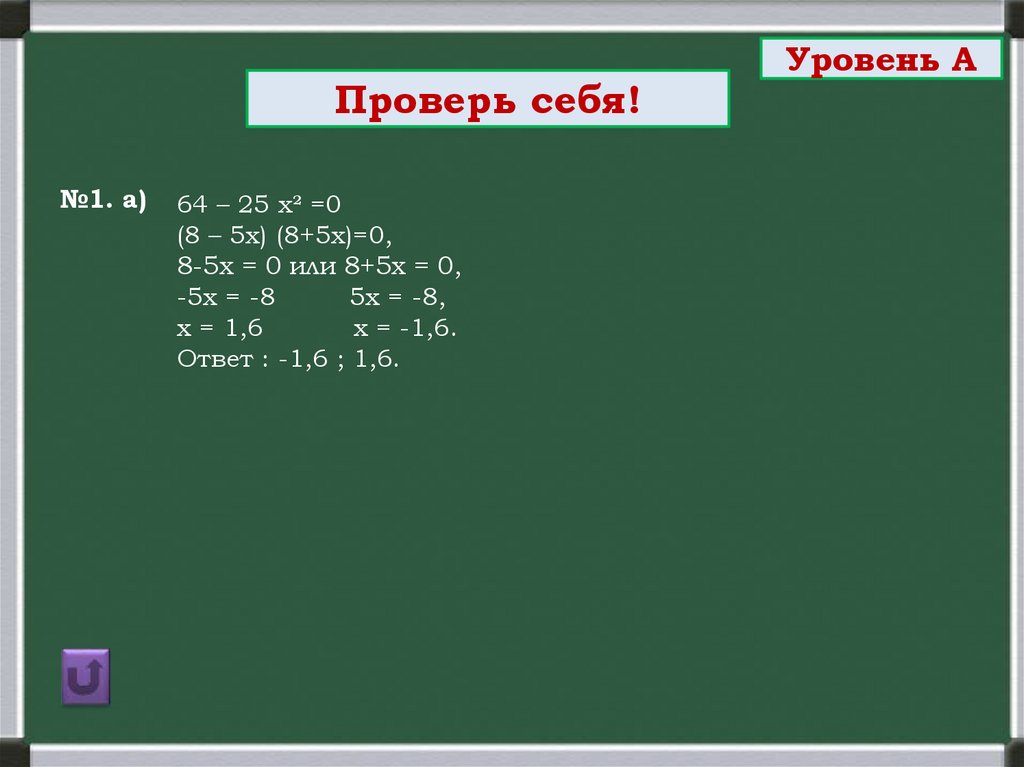
Проверь себя!
№1. а)
64 – 25 х² =0
(8 – 5х) (8+5х)=0,
8-5х = 0 или 8+5х = 0,
-5х = -8
5х = -8,
х = 1,6
х = -1,6.
Ответ : -1,6 ; 1,6.
Уровень А

25.

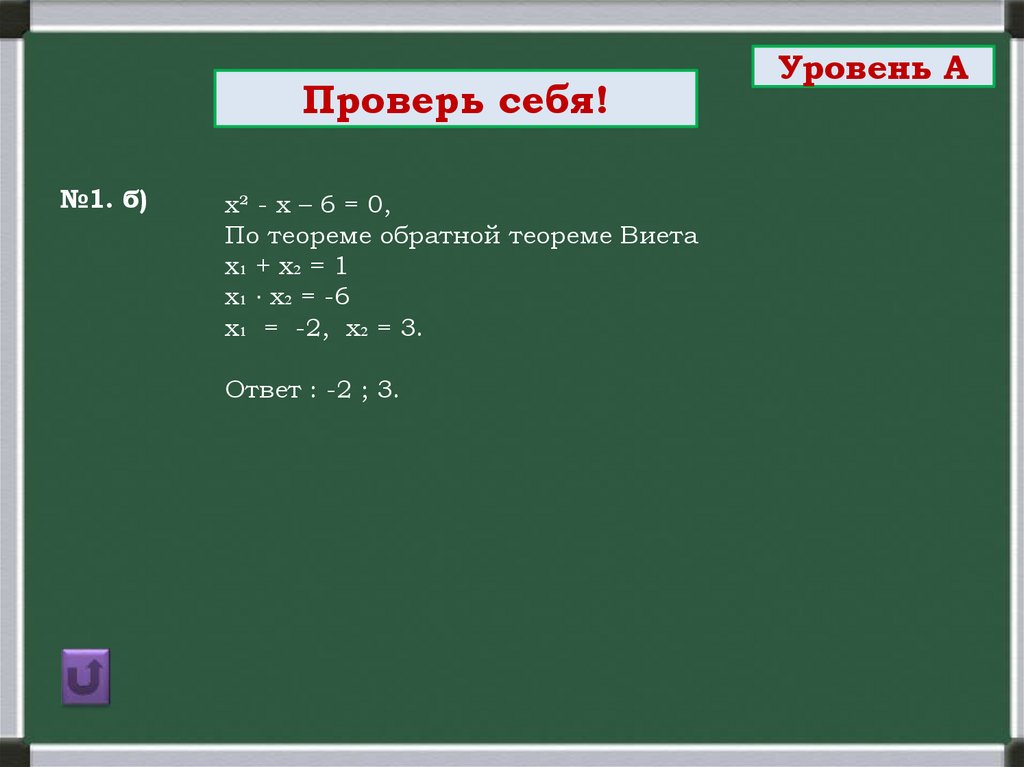
Проверь себя!
№1. б)
х² - х – 6 = 0,
По теореме обратной теореме Виета
х₁ + х₂ = 1
х₁ ∙ х₂ = -6
х₁ = -2, х₂ = 3.
Ответ : -2 ; 3.
Уровень А

26.

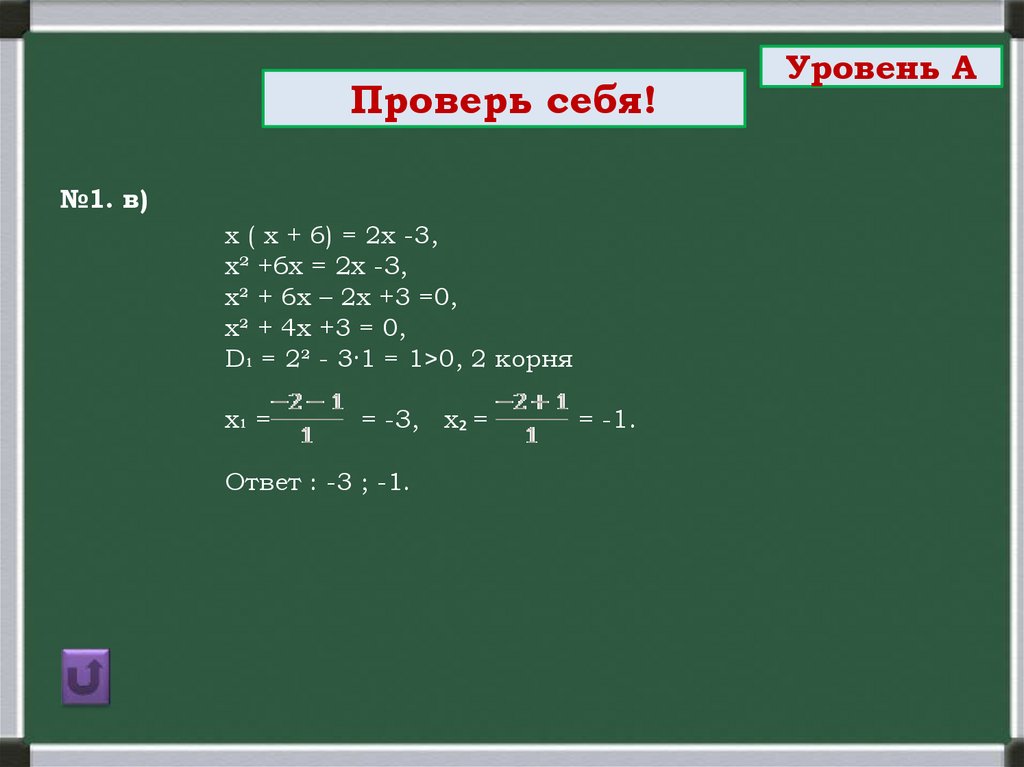
Проверь себя!
№1. в)
х ( х + 6) = 2х -3,
х² +6х = 2х -3,
х² + 6х – 2х +3 =0,
х² + 4х +3 = 0,
D₁ = 2² - 3·1 = 1>0, 2 корня
х₁ =
= -3, х₂ =
Ответ : -3 ; -1.
= -1.
Уровень А

27.

Проверь себя!
Уровень А
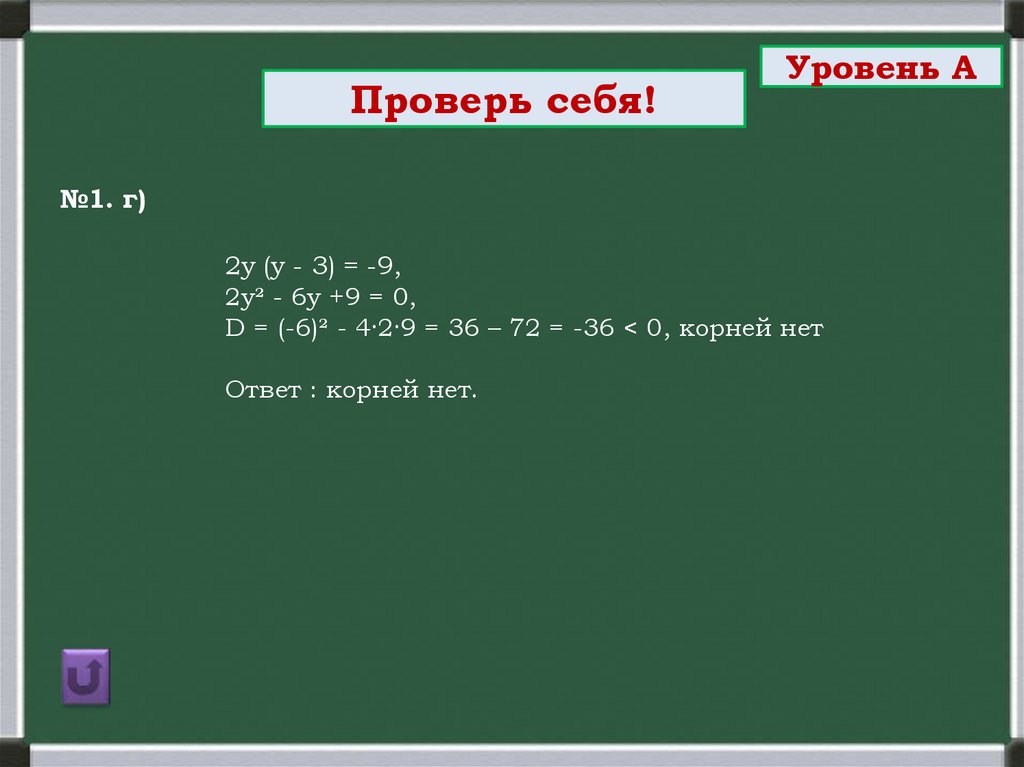
№1. г)
2у (у - 3) = -9,
2у² - 6у +9 = 0,
D = (-6)² - 4·2·9 = 36 – 72 = -36 < 0, корней нет
Ответ : корней нет.

28.

Уровень А
Проверь себя!
№2.
Решение:
Решим уравнение
х(х - 2) = 0
х=0 или х -2 =0,
х = 2.
Ответ: 3 - Б.
По теореме обратной теореме Виета:
х² + 5х – 6 =0,
х₁ + х₂ = -5,
х₁∙ х ₂ = -6,
х₁ = -6 , х₂ = 1.
Ответ: 1-А.
Значит 2-В.
Ответ:
1
2
А
В
3
Б

29.

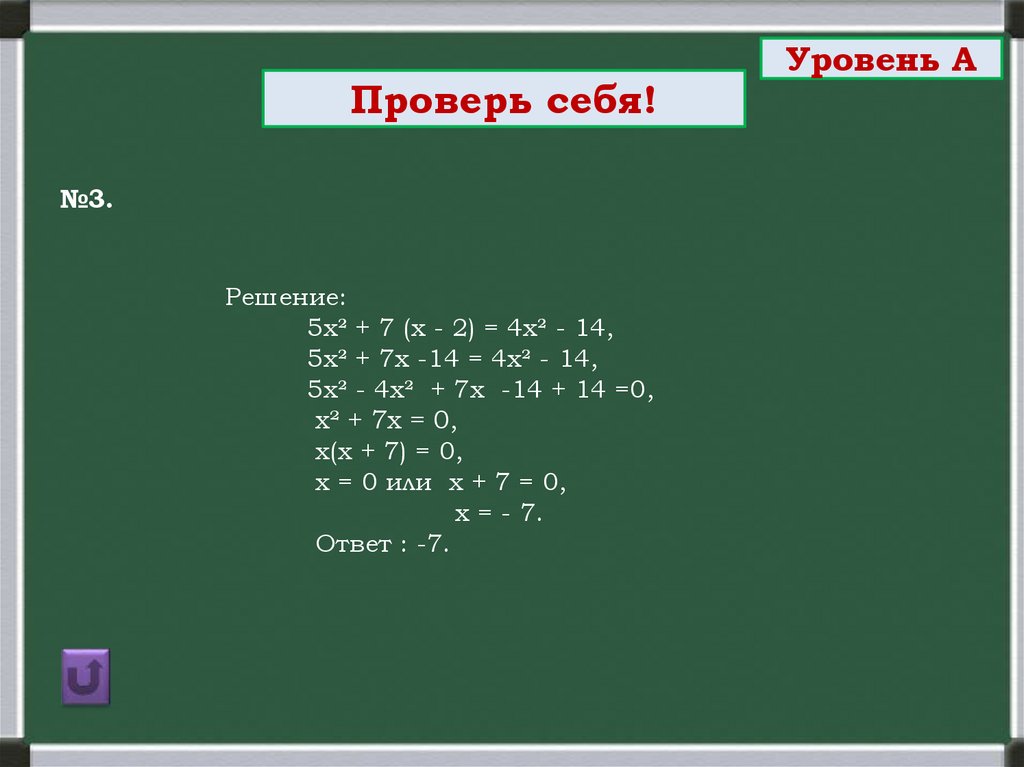
Проверь себя!
№3.
Решение:
5х² + 7 (х - 2) = 4х² - 14,
5х² + 7х -14 = 4х² - 14,
5х² - 4х² + 7х -14 + 14 =0,
х² + 7х = 0,
х(х + 7) = 0,
х = 0 или х + 7 = 0,
х = - 7.
Ответ : -7.
Уровень А

30.

Проверь себя!
Уровень А
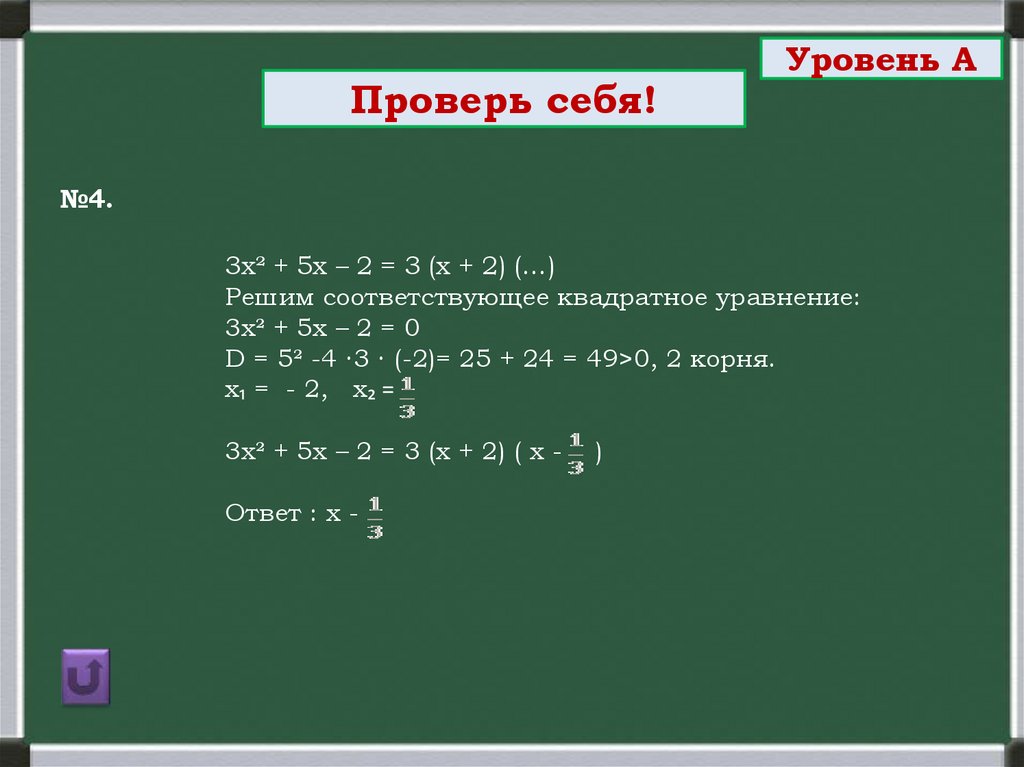
№4.
3х² + 5х – 2 = 3 (х + 2) (…)
Решим соответствующее квадратное уравнение:
3х² + 5х – 2 = 0
D = 5² -4 ∙3 ∙ (-2)= 25 + 24 = 49>0, 2 корня.
х₁ = - 2, х₂ =
3х² + 5х – 2 = 3 (х + 2) ( х Ответ : х -
)

31.

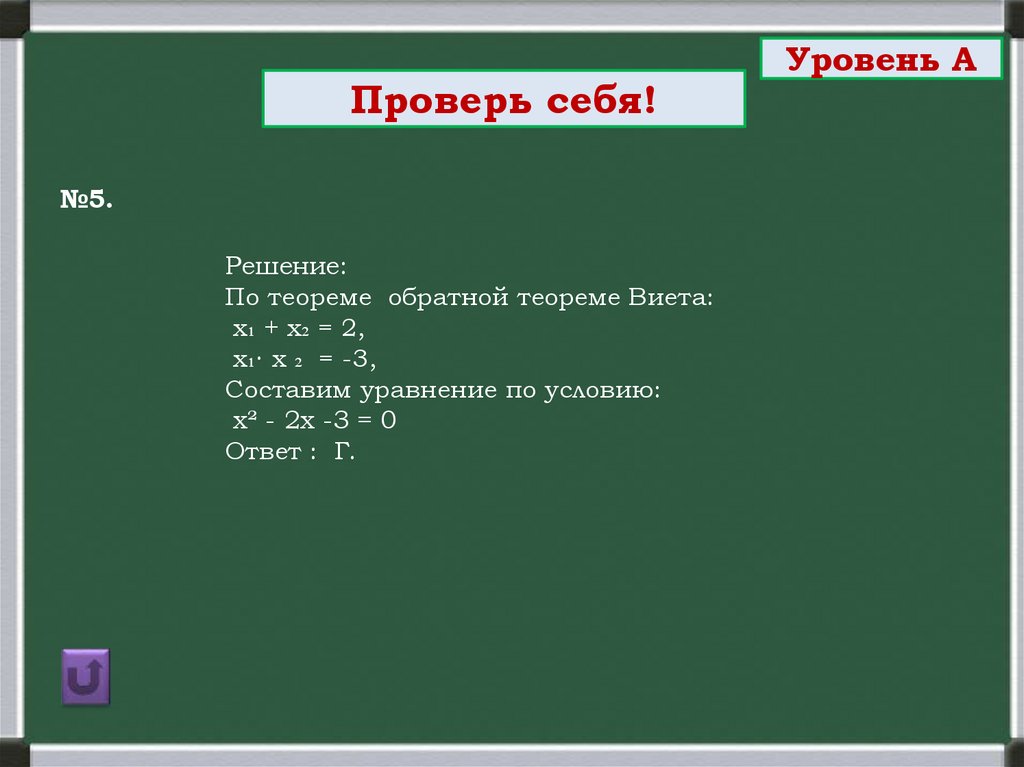
Проверь себя!
№5.
Решение:
По теореме обратной теореме Виета:
х₁ + х₂ = 2,
х₁∙ х ₂ = -3,
Составим уравнение по условию:
х² - 2х -3 = 0
Ответ : Г.
Уровень А

32.

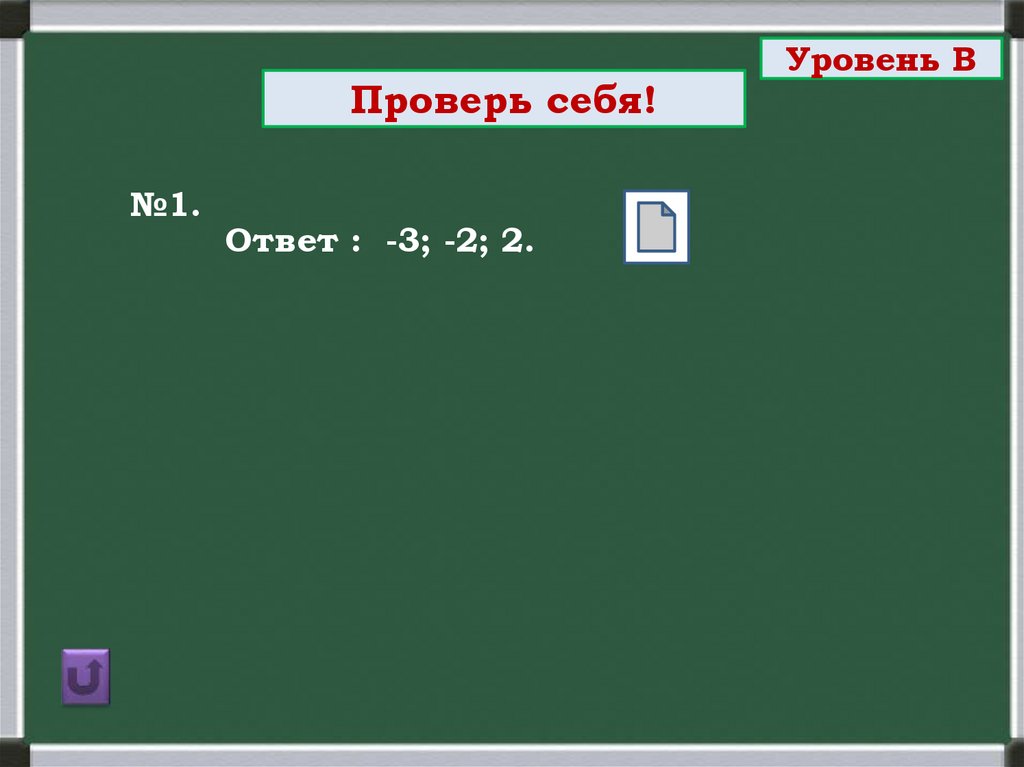
Проверь себя!
№1.
Ответ : -3; -2; 2.
Уровень В

33.

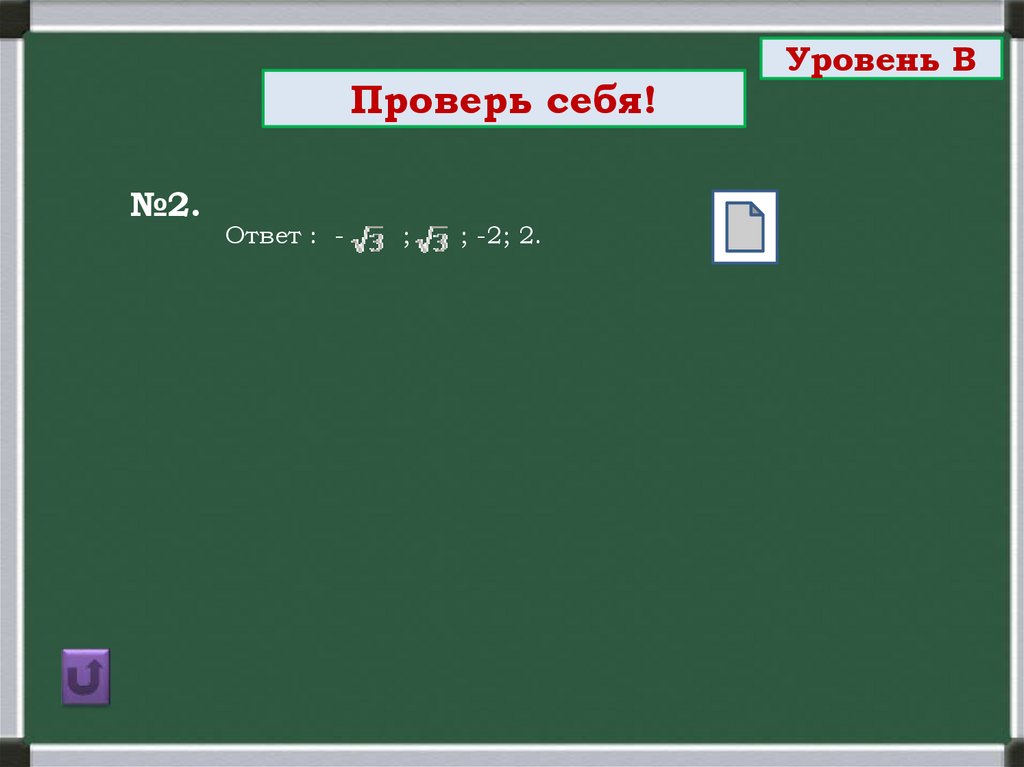
Проверь себя!
№2.
Ответ : -
;
; -2; 2.
Уровень В

34.

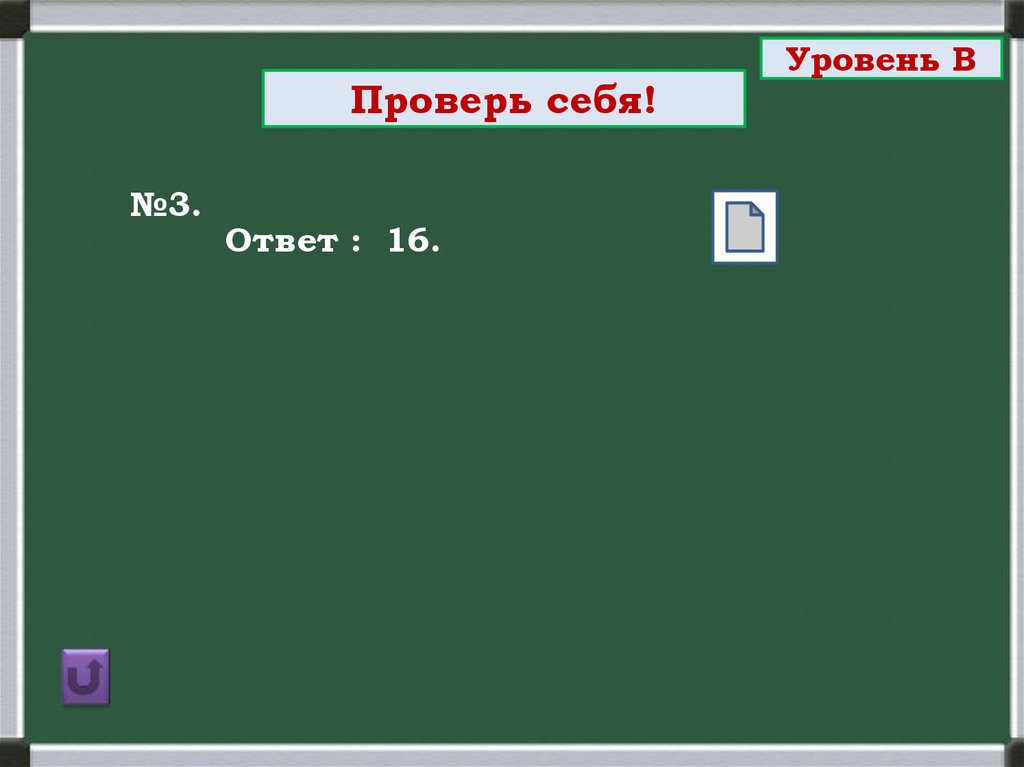
Проверь себя!
№3.
Ответ : 16.
Уровень В

35.

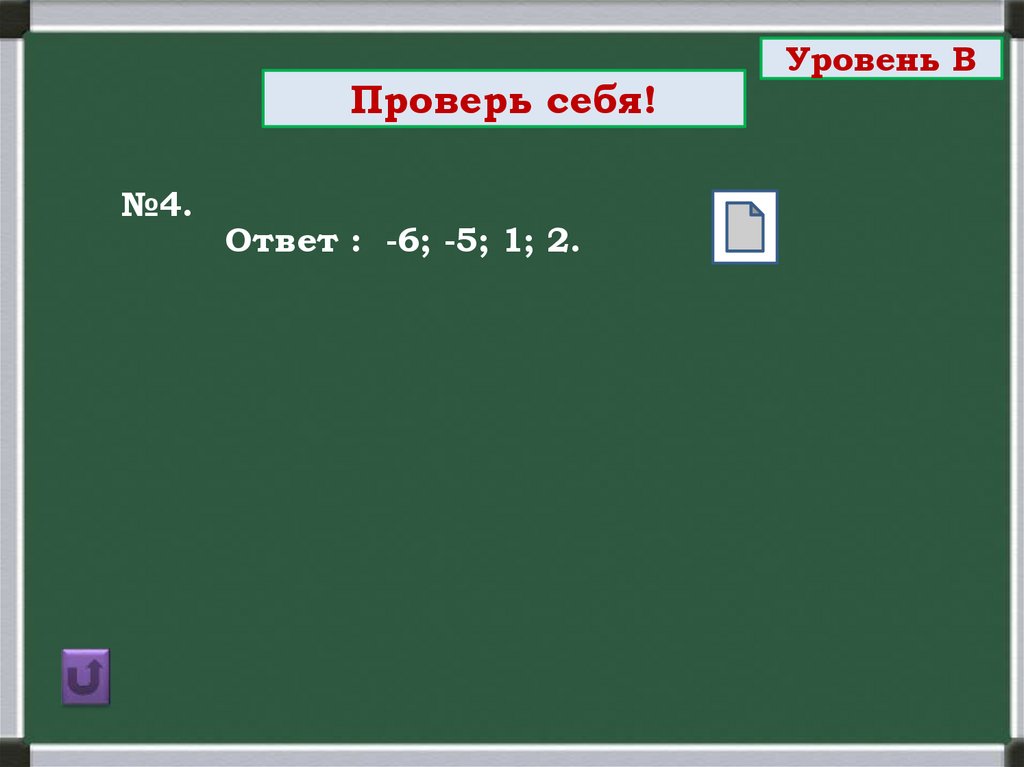
Проверь себя!
№4.
Ответ : -6; -5; 1; 2.
Уровень В

36.

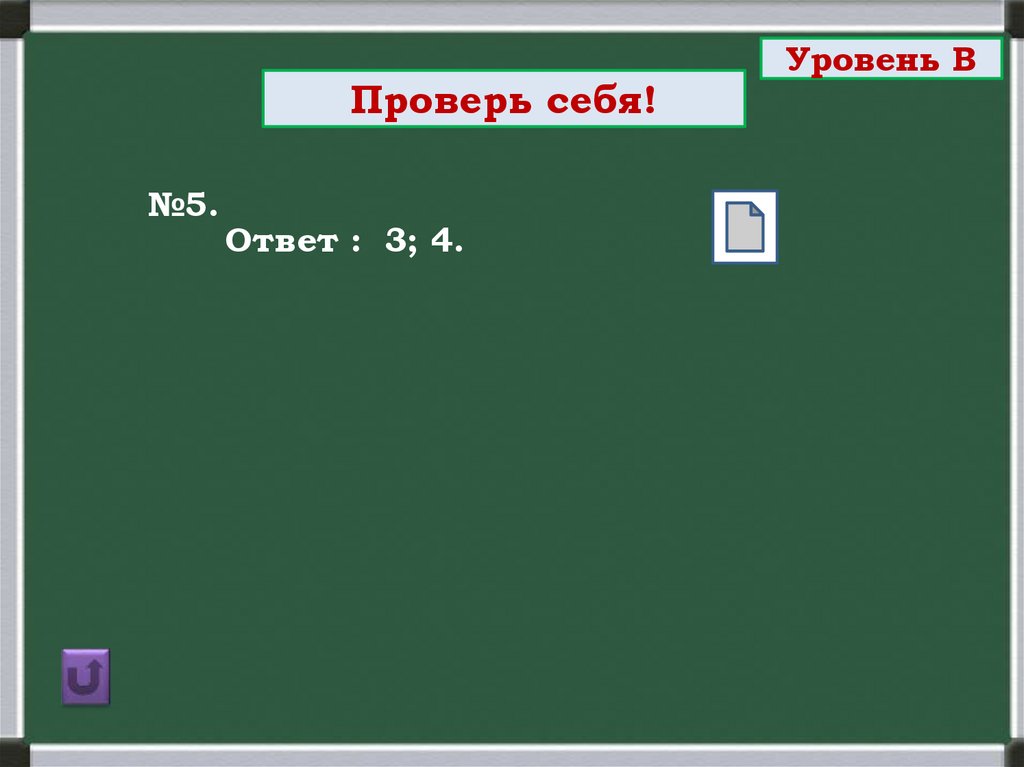
Проверь себя!
№5.
Ответ : 3; 4.
Уровень В

37.

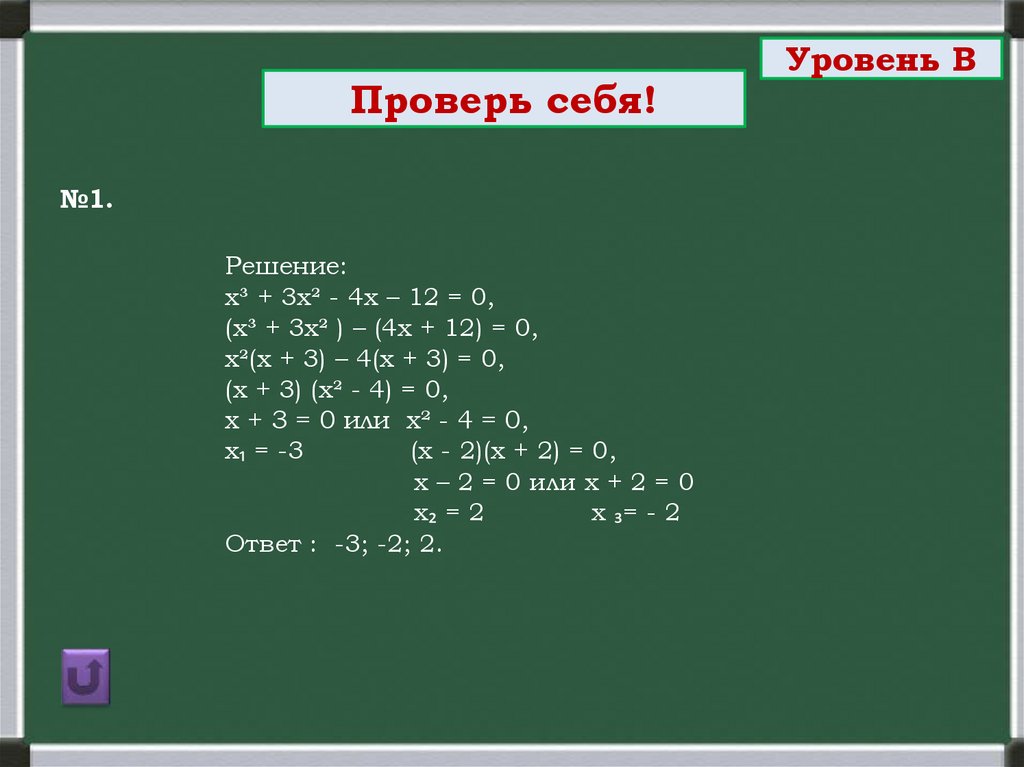
Проверь себя!
№1.
Решение:
х³ + 3х² - 4х – 12 = 0,
(х³ + 3х² ) – (4х + 12) = 0,
х²(х + 3) – 4(х + 3) = 0,
(х + 3) (х² - 4) = 0,
х + 3 = 0 или х² - 4 = 0,
х₁ = -3
(х - 2)(х + 2) = 0,
х – 2 = 0 или х + 2 = 0
х₂ = 2
х ₃= - 2
Ответ : -3; -2; 2.
Уровень В

38.

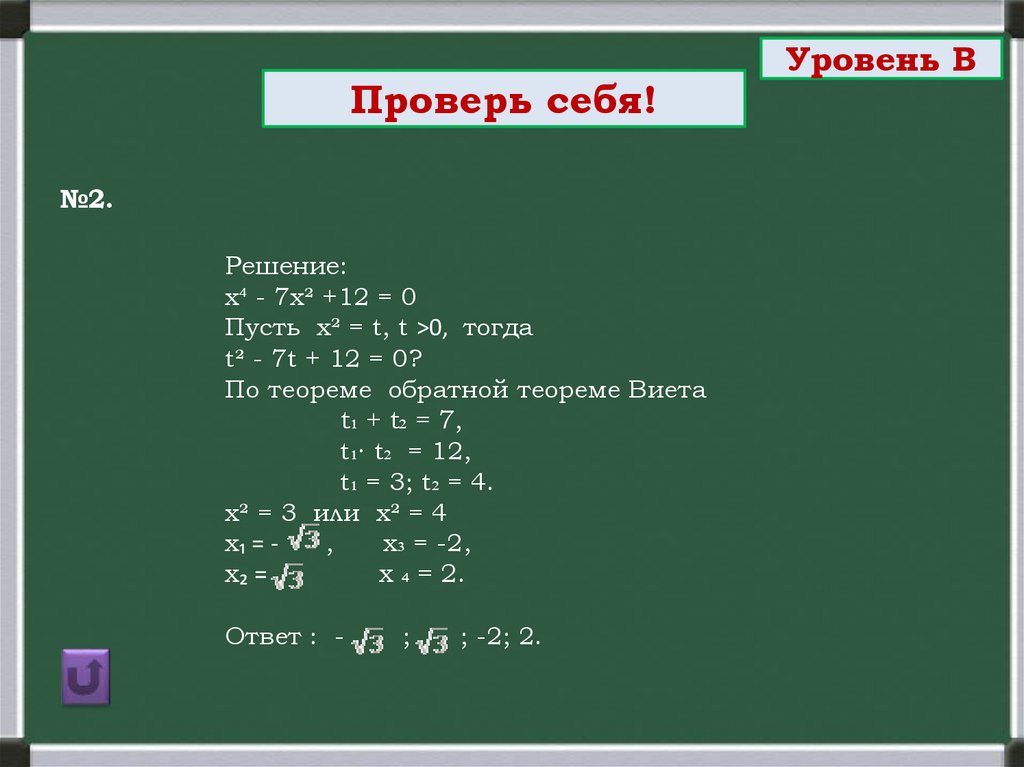
Проверь себя!
№2.
Решение:
х⁴ - 7х² +12 = 0
Пусть х² = t, t >0, тогда
t² - 7t + 12 = 0?
По теореме обратной теореме Виета
t₁ + t₂ = 7,
t₁∙ t₂ = 12,
t₁ = 3; t₂ = 4.
х² = 3 или х² = 4
х₁ = ,
х₃ = -2,
х₂ =
х ₄ = 2.
Ответ : -
;
; -2; 2.
Уровень В

39.

Проверь себя!
Уровень В
№3.
Решение:
х + √х - 20 =0,
(√х )² + √х – 20 = 0,
1) х > 0
2) Пусть √х =t, t>0 тогда
t² + t – 20 = 0,
D = 1 – 4 (-20) = 81>0, 2 корня
t₁ = -5 – не удовлетворяет условию t>0,
t₂ = 4, х = 16.
Ответ : 16.

40.

Проверь себя!
№4.
Уровень В
Решение: (х² + 4х)(х² + 4х - 17) = -60,
Пусть х² + 4х = t, тогда
t (t - 17) = - 60,
t² - 17t + 60 = 0?
По теореме обратной теореме Виета:
t₁ + t₂ = 17,
t₁∙ t₂ = 60,
t₁ = 5; t₂ = 12.
х² + 4х = 5
или
х² + 4х = 12
х² + 4х -5 = 0
х² + 4х -12 = 0
По теореме обратной теореме Виета:
х₁ + х₂ = -4,
х₁ + х₂ = -4,
х₁∙ х₂ = -5,
х₁∙ х₂ = -12,
х₁ = -5; х₂ = 1,
х₃ = -6; х₄ = 2
Ответ : -6; -5; 1; 2.

41.

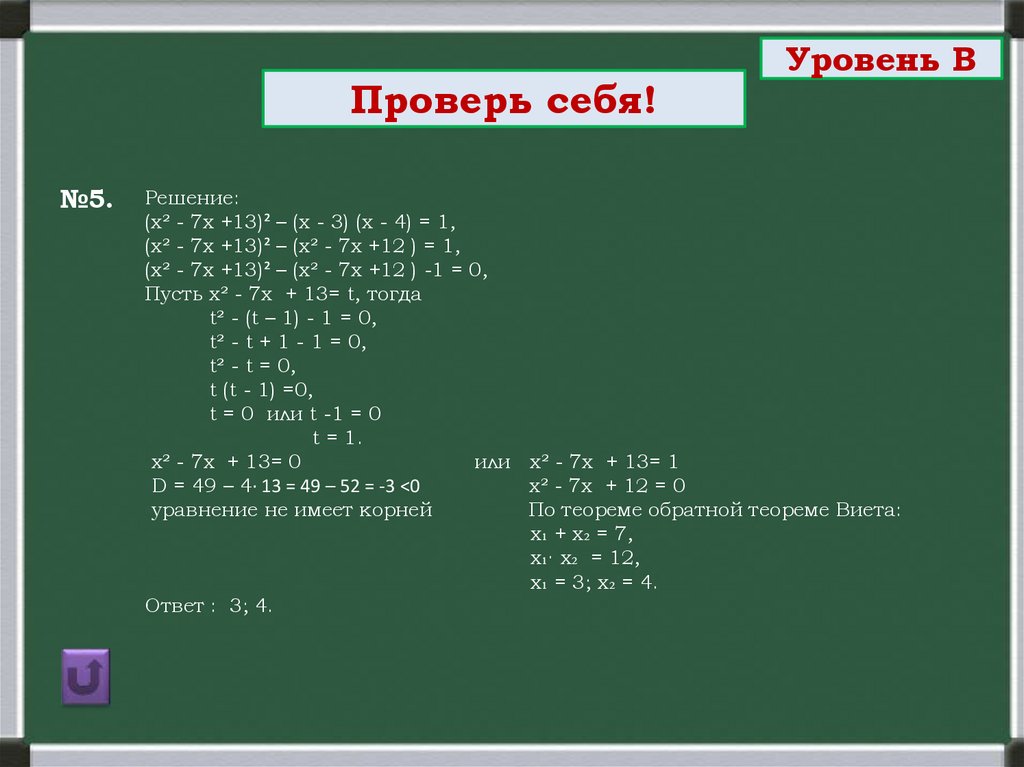
Проверь себя!
№5.
Уровень В
Решение:
(х² - 7х +13)² – (х - 3) (х - 4) = 1,
(х² - 7х +13)² – (х² - 7х +12 ) = 1,
(х² - 7х +13)² – (х² - 7х +12 ) -1 = 0,
Пусть х² - 7х + 13= t, тогда
t² - (t – 1) - 1 = 0,
t² - t + 1 - 1 = 0,
t² - t = 0,
t (t - 1) =0,
t = 0 или t -1 = 0
t = 1.
х² - 7х + 13= 0
или х² - 7х + 13= 1
D = 49 – 4∙ 13 = 49 – 52 = -3 <0
х² - 7х + 12 = 0
уравнение не имеет корней
По теореме обратной теореме Виета:
х₁ + х₂ = 7,
х₁∙ х₂ = 12,
х₁ = 3; х₂ = 4.
Ответ : 3; 4.

42.

Из истории решения
квадратных уравнений.
Уравнения 2-ой степени умели
решать еще в Древнем Вавилоне во
II тысячелетии до н.э. Математики
Древней Греции решали квадратные
уравнения
геометрически;
например, Евклид – при помощи
деления отрезка в среднем и
крайнем
отношениях.
Задачи,
приводящие
к
квадратным
уравнениям, рассматриваются во
многих
древних
математических
рукописях и трактатах.

43.

Из истории решения
квадратных уравнений.
Формула
корней
квадратного
уравнения
«переоткрывалась»
неоднократно.
Один
из
первых
дошедших до наших дней выводов этой
формулы
принадлежит
индийскому
математику Брахмагупте (около 598 г.).
Среднеазиатский ученый ал-Хорезми
(IX в.) в трактате «Китаб аль-джебр валь
-мукабала»
получил
эту
формулу
методом выделения полного квадрата с
помощью
геометрической
интерпретации.

44.

Брахмагупт
(около 598-660 г.г.)
Индийский математик и астроном.
Основное
сочинение
«Усовершенствованное учение Брахмы»
(«Брахмаспхутасиддханта»,
628
г.),
значительная часть которого посвящена
арифметике и алгебре. Брахмагупта,
изложил общее
правило решения
квадратных уравнений, приведенных к
единой канонической форме:
ax2 + bх = с, а> 0. (1)
В уравнении (1) коэффициенты, кроме
а, могут быть и отрицательными.
Правило Брахмагупты по существу
совпадает с нашим.

45.

Евклид
(3 в. До н.э.)
Древнегреческий математик, работал в
Александрии. Главный труд «Начала»(15
книг),
содержит
основы
античной
математики, элементарной геометрии,
теории чисел, общей теории отношений и
метода
определения
площадей
и
объемов, включавшего элементы теории
пределов, оказал огромное влияние на
развитие математики.

46.

Аль-Хорезми
Наибольших успехов в математике достиг
согдиец Мухаммед ибн Муса аль-Хорезми (то
есть, родом из Хорезма - с берегов Сыр-Дарьи).
Он работал в первой половине 9 века и был
любимцем ученейшего из халифов - Маамуна
(сына знаменитого Гаруна ар-Рашида). Главная
книга Хорезми названа скромно: "Учение о
переносах и сокращениях", то есть техника
решения алгебраических уравнений. По-арабски
это звучит "Ильм аль-джебр ва"ль-мукабала";
отсюда произошло наше слово "алгебра".
Другое известное слово - "алгоритм", то есть
четкое правило решения задач определенного
типа - произошло от прозвания "аль-Хорезми".

47.

Спасибо за работу с нашим
электронным справочником!
Содержание
справочника