Программирование в Mathcad. Численное интегрирование. Лабораторная работа №8

1.

Программирование в Mathcad. Численное
интегрирование
Лабораторная работа №8

2.

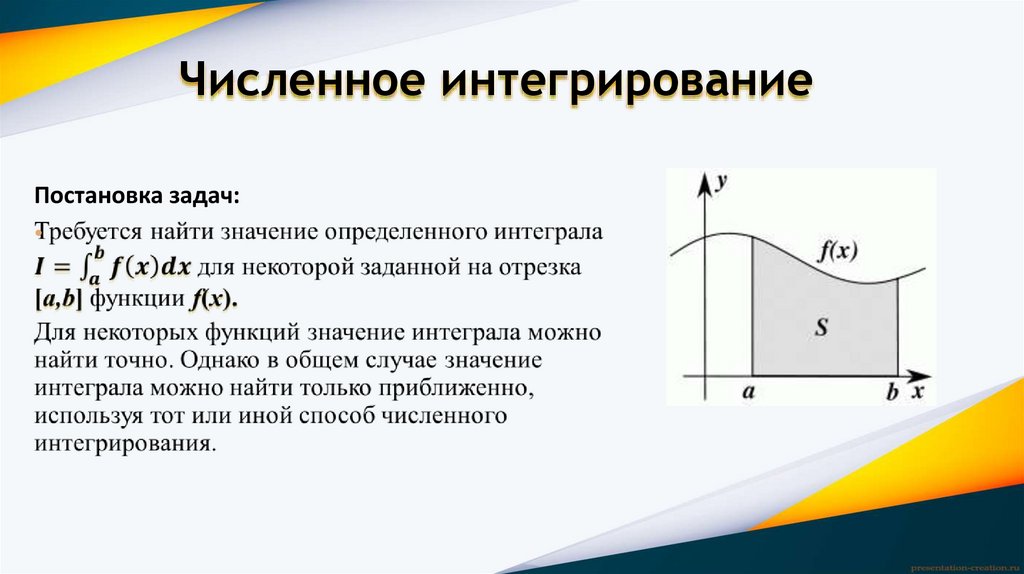
Численное интегрирование
Постановка задач:

3.

4.

5.

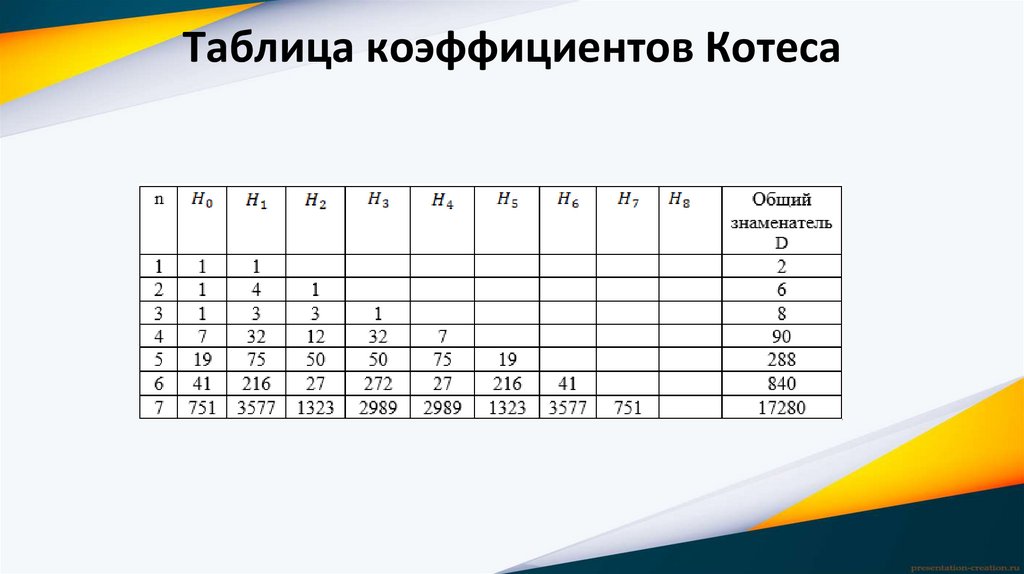
Таблица коэффициентов Котеса

6.

Cмысл квадратурных формул Гаусса состоит в
том, чтобы при наименьшем возможном числе
узлов точно интегрировать многочлены
наивысшей возможной степени
1
n
1
i 1
f
(
t
)
dt
A
f
(
t
)
i
i

7.

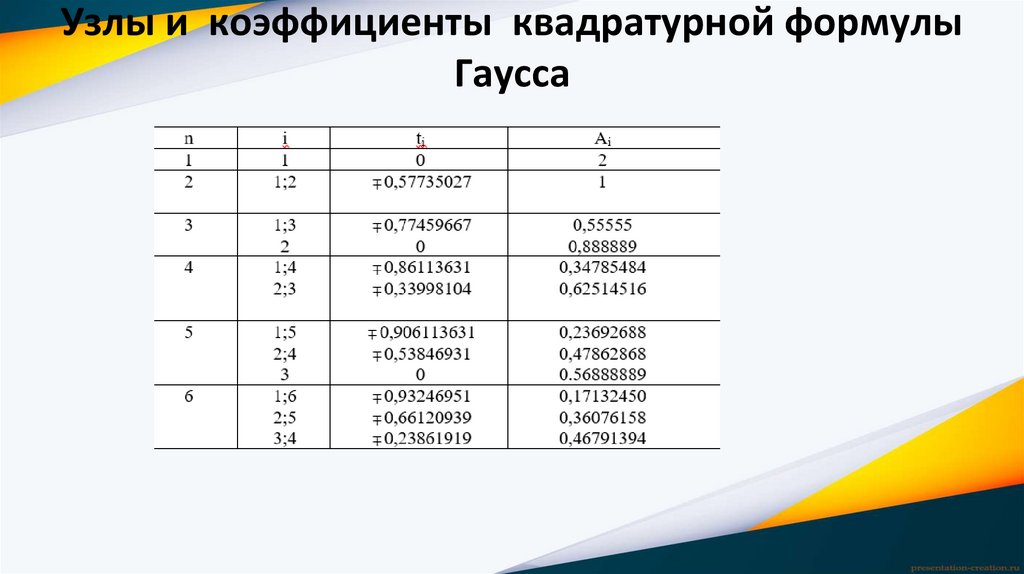
Узлы и коэффициенты квадратурной формулы
Гаусса

8.

Задание №1
Найти приближенное значение интеграла
заданной функции f(x) по формуле
трапеции.(N=2)
f(x)=sin(x)

9.

Решение:

10.

Задание №2
Найти приближенное значение интеграла
заданной функции f(x) по формуле
трапеции.(N=3)
f(x)=sin(x)

11.

Решение:

12.

Задание №3
Найти приближенное значение интеграла
заданной функции f(x) по формуле
прямоугольников (левых, правых, средних).
f(x)=sin(x)

13.

Решение:

14.

Решение:

15.

Решение:

16.

Задание №4
Найти приближенное значение интеграла
заданной функции f(x) по формуле
Гаусса.(N=2)
f(x)=sin(x)

17.

Решение:

18.

Задание №5
Найти приближенное значение интеграла
заданной функции f(x) по формуле Гаусса.(N=3)
f(x)=sin(x)

19.

Решение: