Похожие презентации:
Физические основы радиоэлектроники
1.
Лекция 22022
1
2.
23.
Самописец пишет сам3
4.
Песня появилась в XIII или XIV веке либо в Гейдельбергском, либо вПарижском университете (поэт Себастьян Брант упоминает
гимн 1267 года под названием «Gaudeamus igitur»).
4
5.
sin a sin b1
cos( a b) cos( a b)
2
!
0
Эффективным
значением
переменного
тока называется
значение
постоянного
тока, который
производит
одинаковое
тепловое
действие с
нашим
переменным.
0
5
6.
U0U эфф
0.7 U 0
2
6
7.
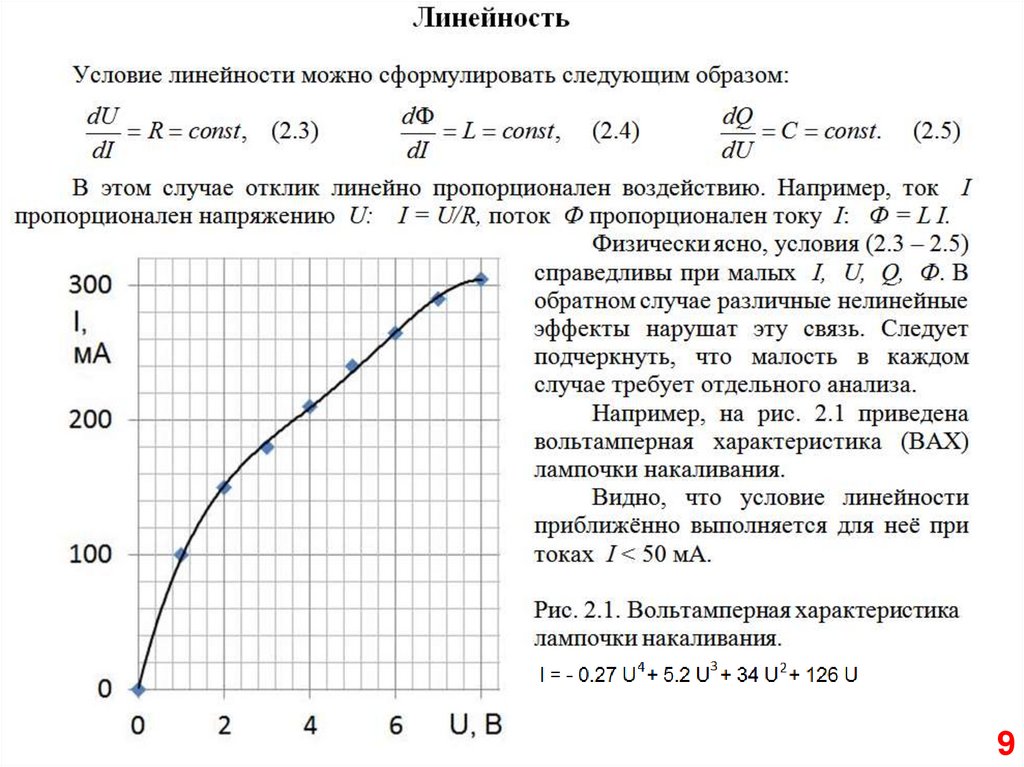
78.
89.
910.
Анализ линейных системВ общем случае анализ линейной стационарной системы
сводится к решению системы линейных дифференциальных
(или интегро-дифференциальных) уравнений с постоянными
коэффициентами.
Стационарная система - это система, в которой сдвиг
входного сигнала во времени приводит к такому же сдвигу
выходного сигнала.
Для получения этих уравнений используются известные
правила Кирхгофа.
10
11.
Первое правило Кирхгофа: алгебраическая сумма токов,сходящихся в узле, равна нулю.
Узлом называется точка, в которой сходится более чем два
проводника.
Это правило вытекает из закона сохранения заряда.
Число уравнений, составленных по первому правилу Кирхгофа,
должно быть на одно меньше, чем число узлов в исследуемой
цепи.
Этим обеспечивается линейная независимость получаемых
уравнений.
Второе правило Кирхгофа: для любого замкнутого контура
алгебраическая сумма всех падений напряжения равна сумме
всех ЭДС в этом контуре.
При составлении уравнений согласно второму правилу
Кирхгофа токам и ЭДС нужно приписывать знаки в
соответствии с выбранным направлением обхода.
11
12.
Правила Кирхгофа12
13.
Метод эквивалентного генератораДля анализа сложных линейных цепей иногда применяется метод эквивалентного
генератора, основанный на теореме об активном двухполюснике, называемой
также теоремой Гельмгольца-Тевенена, (H.Helmholtz, L.Thévenin), позволяющий
определить ток в одной ветви сложной линейной схемы, не находя токи в остальных
ветвях.
Рис. 2.6.
Выделенную часть схемы (А) заменяем
двухполюсником с той же буквой.
!
Любую линейную схему внутри двухполюсника А
можно заменить простой эквивалентной схемой с
генератором напряжения Eg и внутренним
сопротивлением Rg .
13
14.
Пользуясь этим методом, любой сколь угодно сложный активныйдвухполюсник можно представить эквивалентным генератором, ЭДС
которого равна напряжению холостого хода на зажимах двухполюсника.
1. Внутреннее сопротивление равно входному сопротивлению
пассивного двухполюсника со стороны тех же зажимов. При определении
внутреннего сопротивления все источники должны быть заменены
своими внутренними сопротивлениями, источники ЭДС
закорачиваются, а источники тока размыкаются.
2. Можно также найти внутреннее сопротивление, поделив эквивалентную
ЭДС на ток короткого замыкания
Аналогично находятся параметры активного двухполюсника и при
синусоидальном токе; только в этом случае необходимо заменить
сопротивления комплексными импедансами,
а Eg – комплексным Ẽg .
14
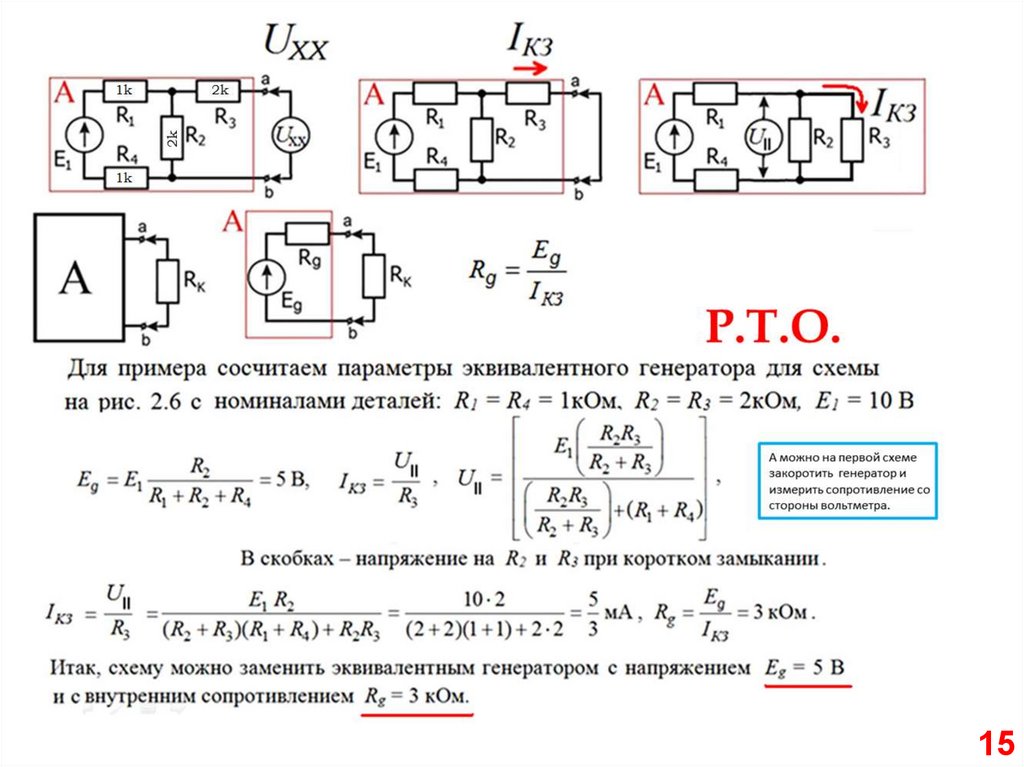
15.
1516.
Если воспользоваться первым способом, то этот же результатможно получить в уме.
16
17.
Принцип суперпозицииДля линейных стационарных систем справедлив
принцип суперпозиции:
если в цепи есть несколько источников тока или напряжения,
то можно рассчитать отклик системы на каждый источник
отдельно. Тогда отклик системы в целом будет просто равен
сумме отдельно рассчитанных откликов.
Каждый источник не влияет на другие, а работает независимо.
Хотелось бы подчеркнуть, что принцип суперпозиции
справедлив только в линейных системах.
Исключение источников выполняют следующим образом:
источники ЭДС заменяют идеальными проводниками,
источники тока – разрывами цепи.
17
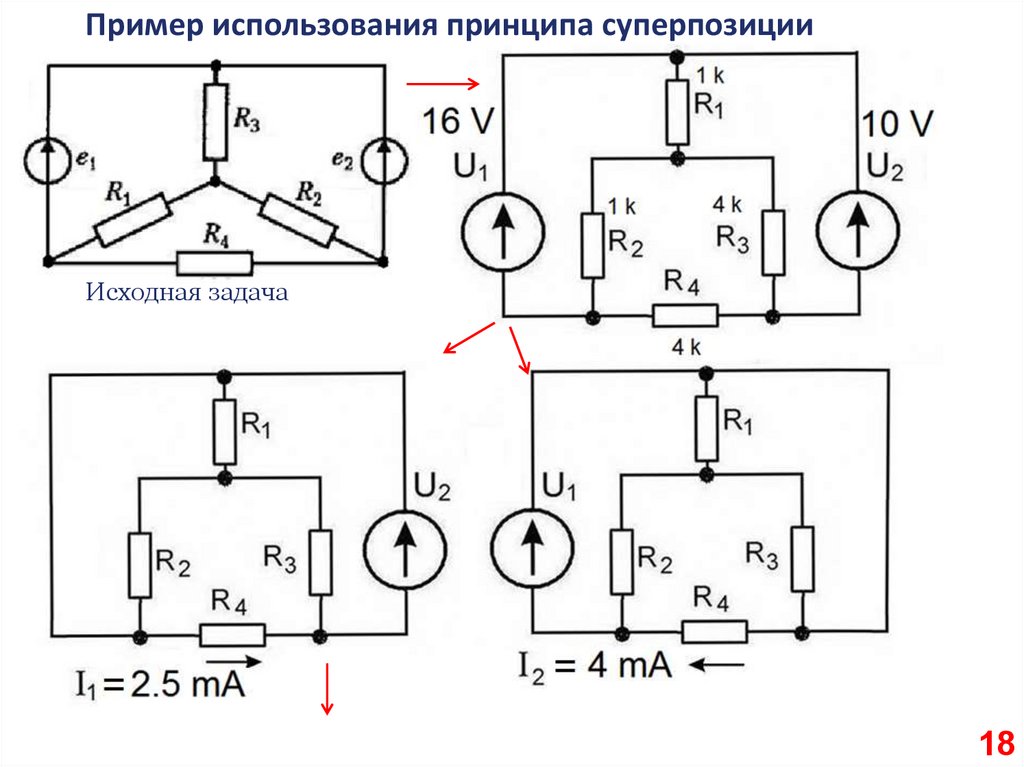
18.
Пример использования принципа суперпозицииИсходная задача
18
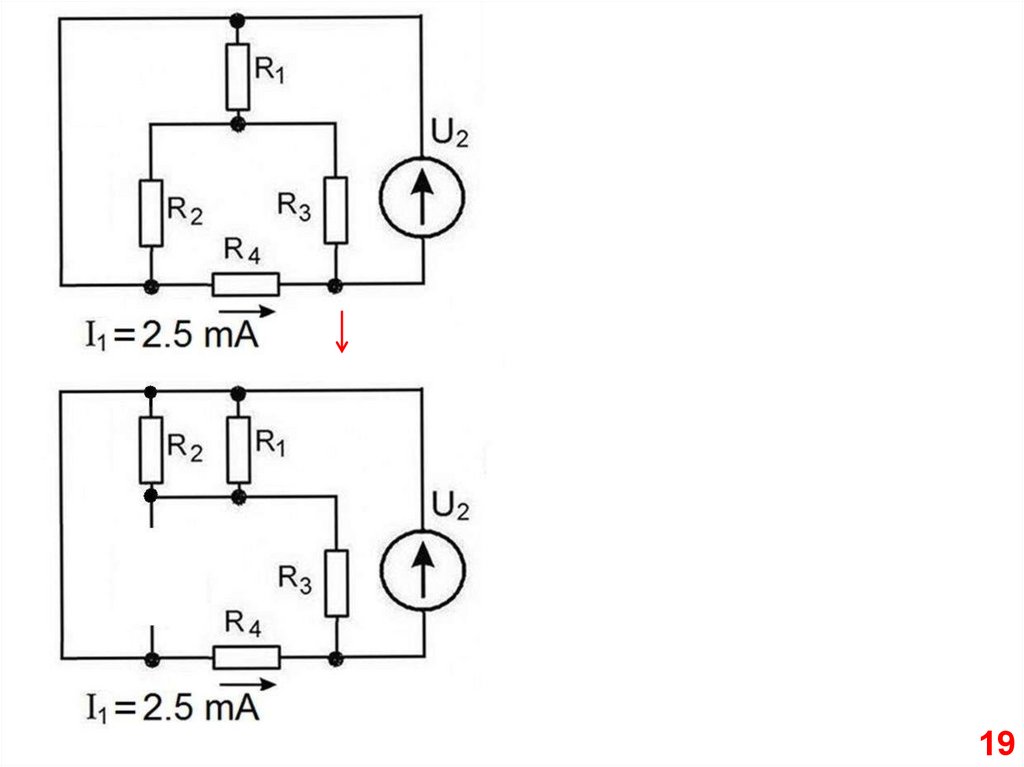
19.
1920.
!20
21.
2122.
1921Charles Proteus Steinmetz, Carl August Rudolph Steinmetz
John Carson
22
23.
a 2 +b2 = AРис. 2.8.
23
24.
2425.
Вращение можно увидеть воочию при помощи программки на Матлабе.clc; % чистит окно команд
FC=[1,1,1]; hFigure=gcf; set(hFigure, 'Color', FC) % удаляют рамку графика
title('exp(+ i \omega t)', 'FontName', 'Times New Roman', 'FontSize',
48,'FontAngle', 'italic'); % заголовок, omega – круговая частота
tic;pause(2);toc; % время для прочтения заголовка
for t = 0:0.04:2*pi; axis([-1.2 1.2 -1 1]) % границы области графика
x=-sin(t); y=cos(t);
h = plot(x,y,'b.'); hold on; pause(0.02)
end; pause(1)% 1 сек
clf; % чистит графическое окно
title('exp(- i \omega t)', 'FontName', 'Times New Roman', 'FontSize', 48,
'FontAngle', 'italic');
tic;pause(2);toc;
for t = 0:0.04:2*pi; axis([-1.2 1.2 -1 1]);
x=sin(t); y=cos(t); h = plot(x,y,'r.'); hold on; pause(0.02)
end; pause(1); clf;
25
26.
Tom Sawyer"Say - what is dead cats good for, Huck?“
Huck Finn
"Good for? Cure warts with.“
“Скажи, для чего нужно представление
синусоидального переменного тока
в комплексной форме?”
“Для чего? Упрощать решение уравнений.”
26
27.
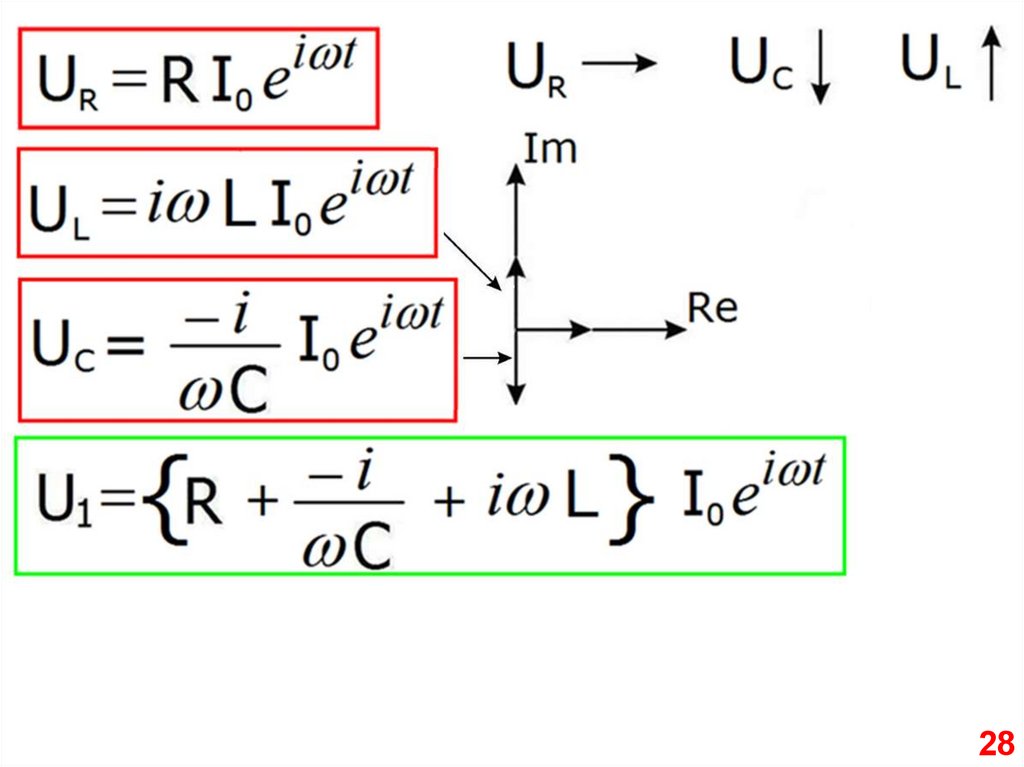
2728.
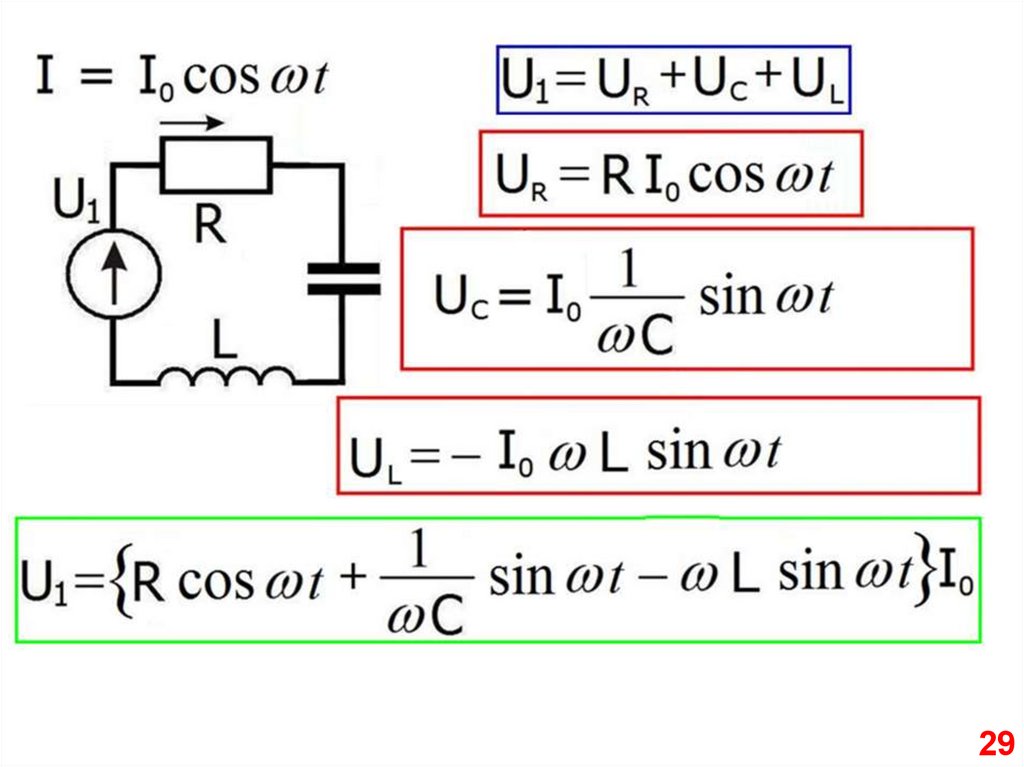
2829.
2930.
Этопроще!
30
31.
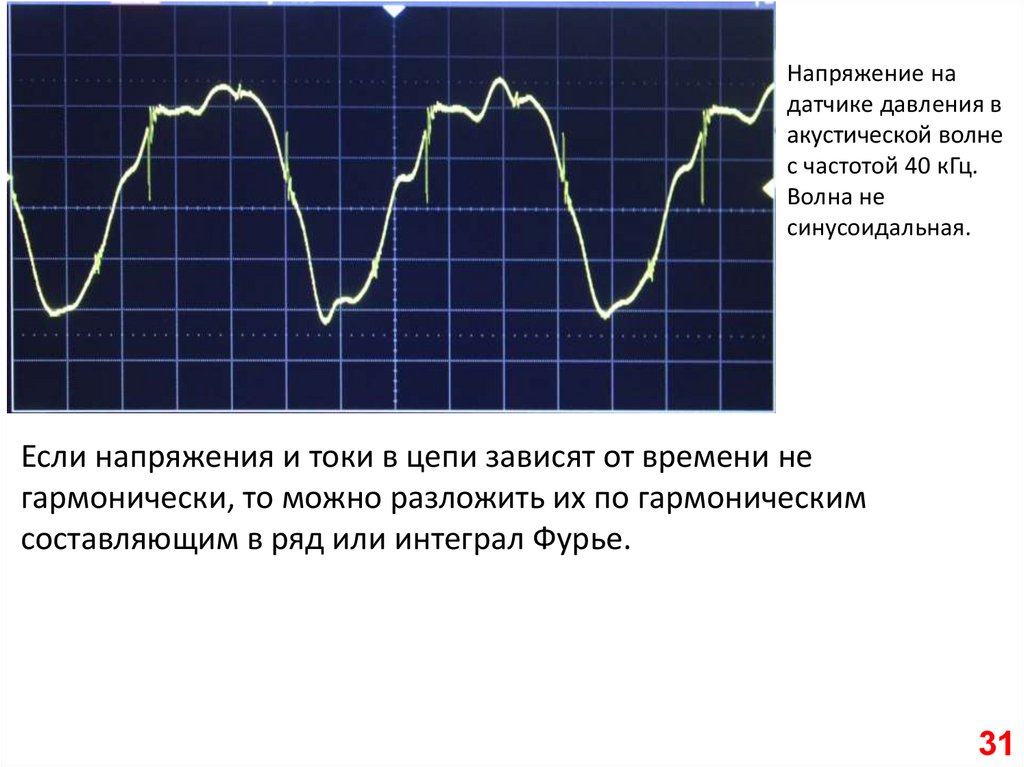
Напряжение надатчике давления в
акустической волне
с частотой 40 кГц.
Волна не
синусоидальная.
Если напряжения и токи в цепи зависят от времени не
гармонически, то можно разложить их по гармоническим
составляющим в ряд или интеграл Фурье.
31
32.
3233.
3334.
Oliver Heaviside Telegrapher's Equations.34
35.
3536.
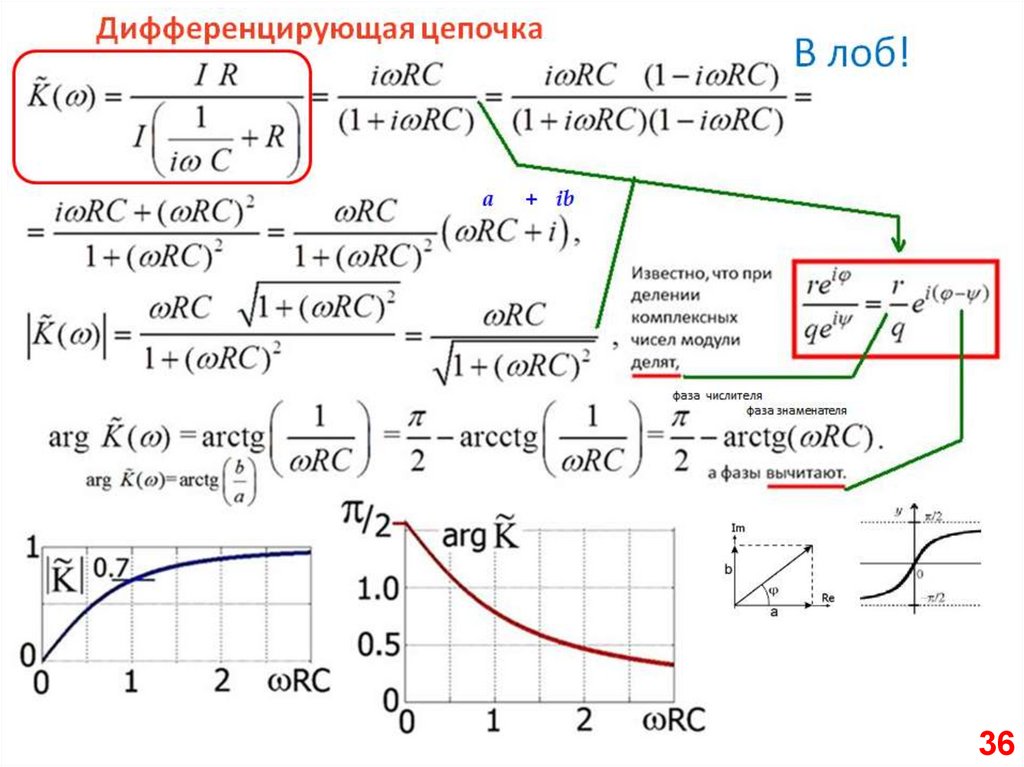
3637.
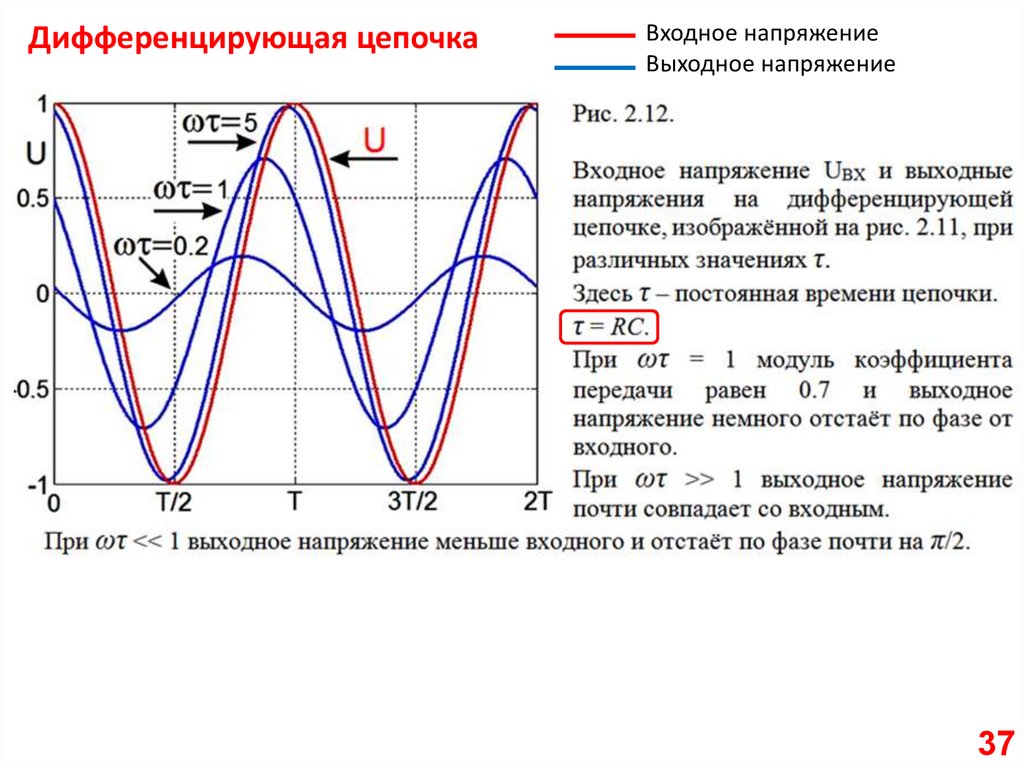
Дифференцирующая цепочкаВходное напряжение
Выходное напряжение
37
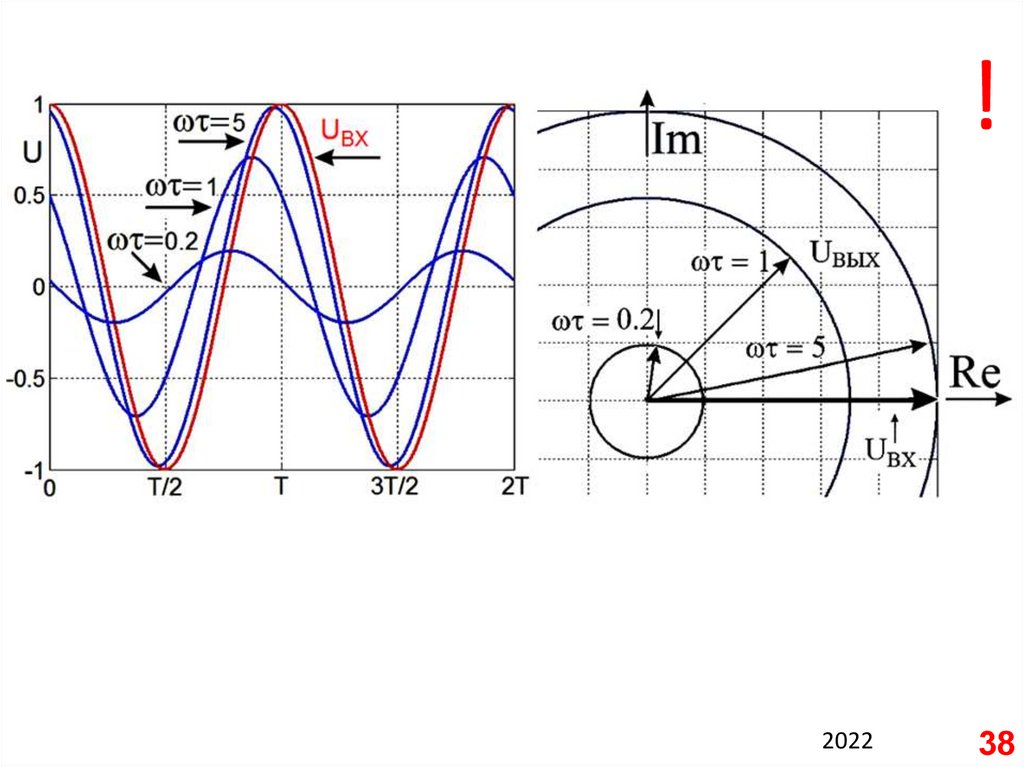
38.
!2022
38
39.
Программа TINA 9.0Toolkit for Interactive Network Analysis
Дифференцирующая цепочка
7.07 5.65 4.26
!
39
40.
4041.
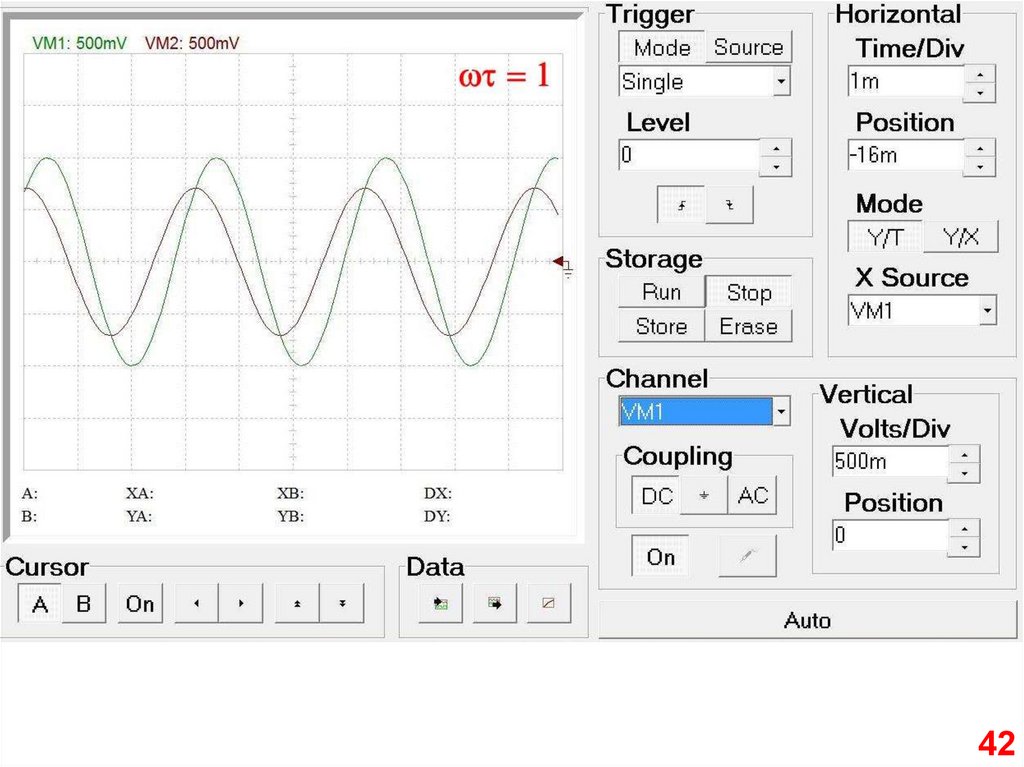
4142.
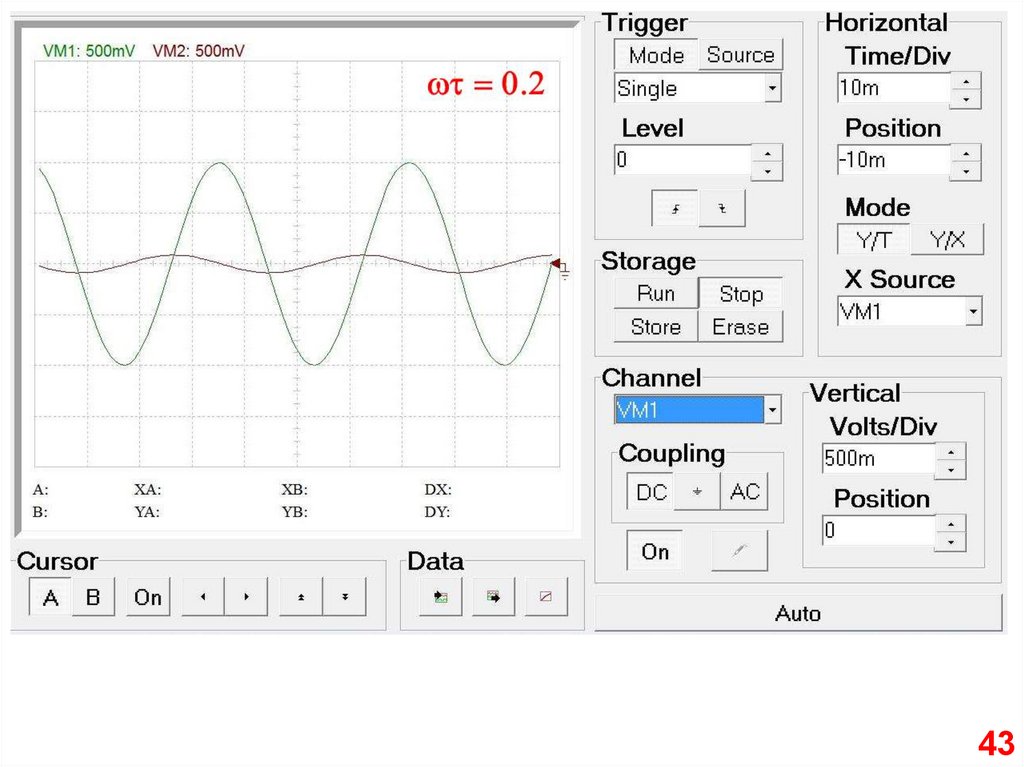
4243.
4344.
4445.
4546.
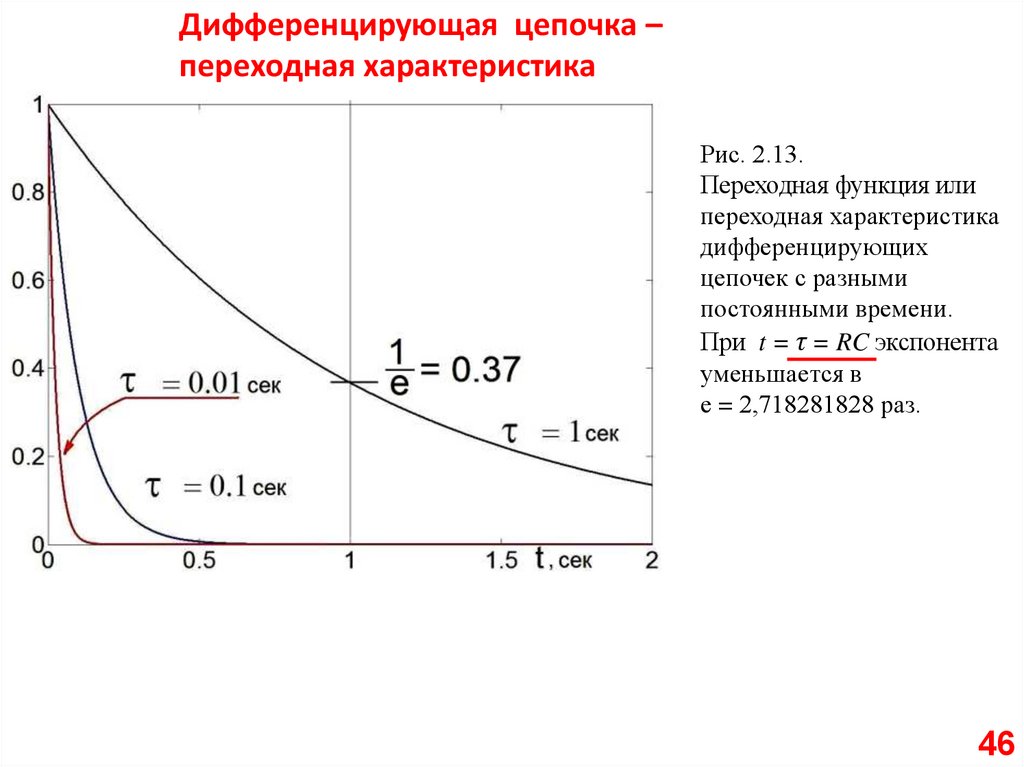
Дифференцирующая цепочка –переходная характеристика
Рис. 2.13.
Переходная функция или
переходная характеристика
дифференцирующих
цепочек с разными
постоянными времени.
При t = τ = RC экспонента
уменьшается в
е = 2,718281828 раз.
46
47.
Рис. 2.11.47
48.
4849.
4950.
The END50







































 Физика
Физика








