Основные способы преобразования графиков функций

1. Основные способы преобразования графиков функций

2. цели для выбора:

цели для выбора
:
- учиться иметь и высказывать собственное мнение;
- развивать умение учиться самостоятельно
- узнать что-то новое о графиках; мне это интересно;
- узнать что-то новое, потому что мне это пригодится
в дальнейшей учебе;
• - отрабатывать умение выполнять известные мне
математические операции.

3. Элементарные функции

• Основными элементарными
функциями называются следующие
функции:
степенная функция
y x , где а R
показательная функция
y a , где а 0; a 1
логарифмическая функция
x
,
y log a x, где а 0; a 1
тригонометрические функции
y sin x
21.01.2024
y cos x
y tg x
y ctg x

4.

• В чистом виде основные элементарные
функции встречаются, к сожалению, не так
часто. Гораздо чаще приходится иметь дело с
элементарными функциями, полученными из
основных элементарных при помощи
добавления констант и коэффициентов. Графики
таких функций можно строить, применяя
геометрические преобразования к графикам
соответствующих основных элементарных
функций (или переходить к новой системе
координат).

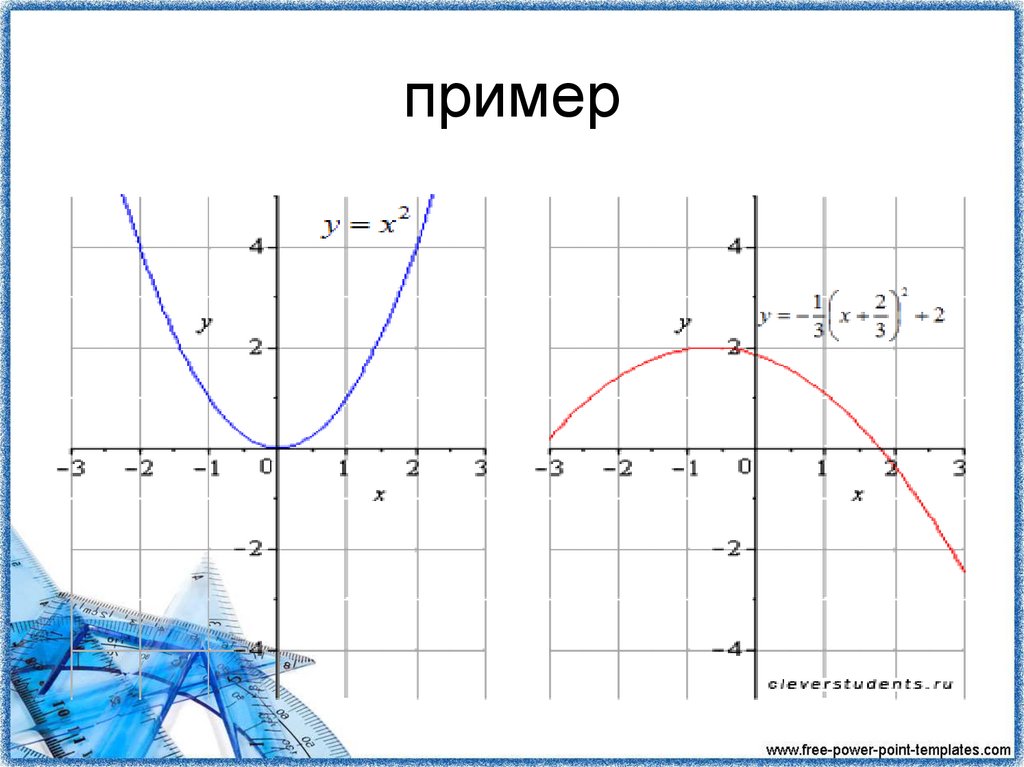
5. пример

6.

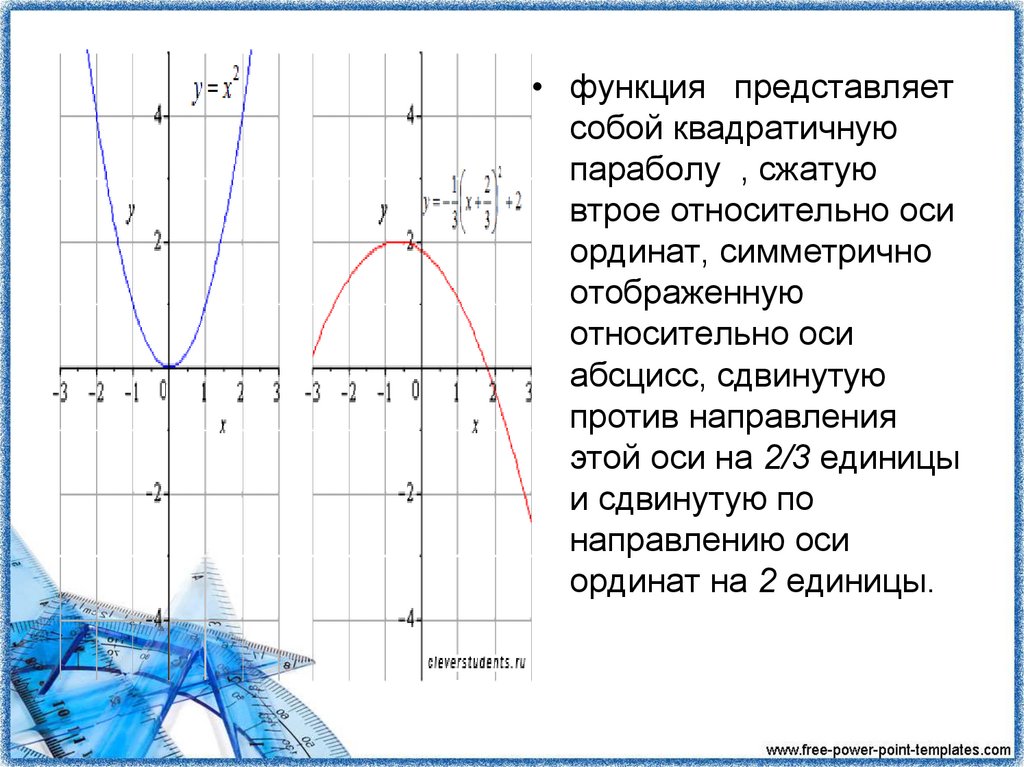
• функция представляет
собой квадратичную
параболу , сжатую
втрое относительно оси
ординат, симметрично
отображенную
относительно оси
абсцисс, сдвинутую
против направления
этой оси на 2/3 единицы
и сдвинутую по
направлению оси
ординат на 2 единицы.

7.

Давайте разберемся в
этих геометрических
преобразованиях графика функции
пошагово на конкретных примерах.

8. Практическая работа

– сдвигом вдоль осиOy на ______(a) единиц (вверх, еслиa >0, и вниз, еслиa <0;
– сдвигом вдоль осиOx на ____(b )единиц (вправо, еслиb >0 ,и влево,
если b <0 )
– растяжением вдоль осиOy в _____(k) раз;
– сжатием по осиOx в_____(m) раз;
– симметричным отражением относительно осиOx ;
– симметричным отражением относительно осиOy ;
- следующим образом: часть графика, расположенная нениже оси Ox ,
остается без изменений, а «нижняя» часть графика симметрично
отражается относительно оси Ox ;
- следующим образом: правая часть графика (приx ≥0 )
остается без изменений, а вместо «левой» строится симметричное отражение
«правой» относительно оси Oy .

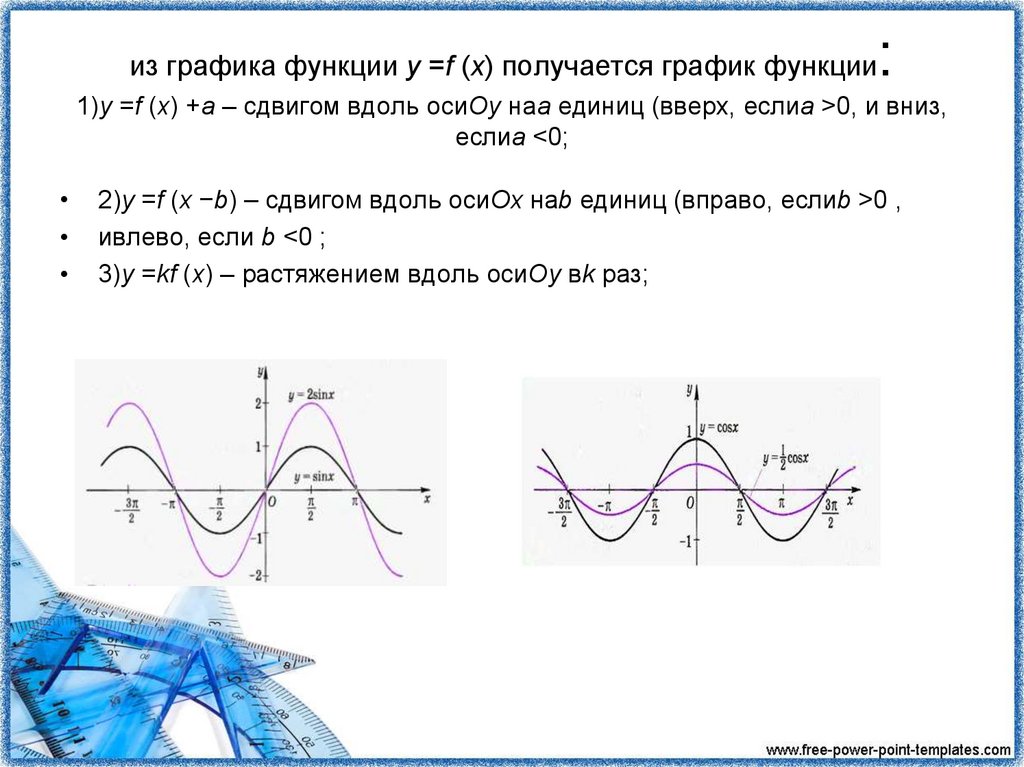
9. из графика функции y =f (x) получается график функции: 1)y =f (x) +a – сдвигом вдоль осиOy наa единиц (вверх, еслиa >0, и вниз,

:
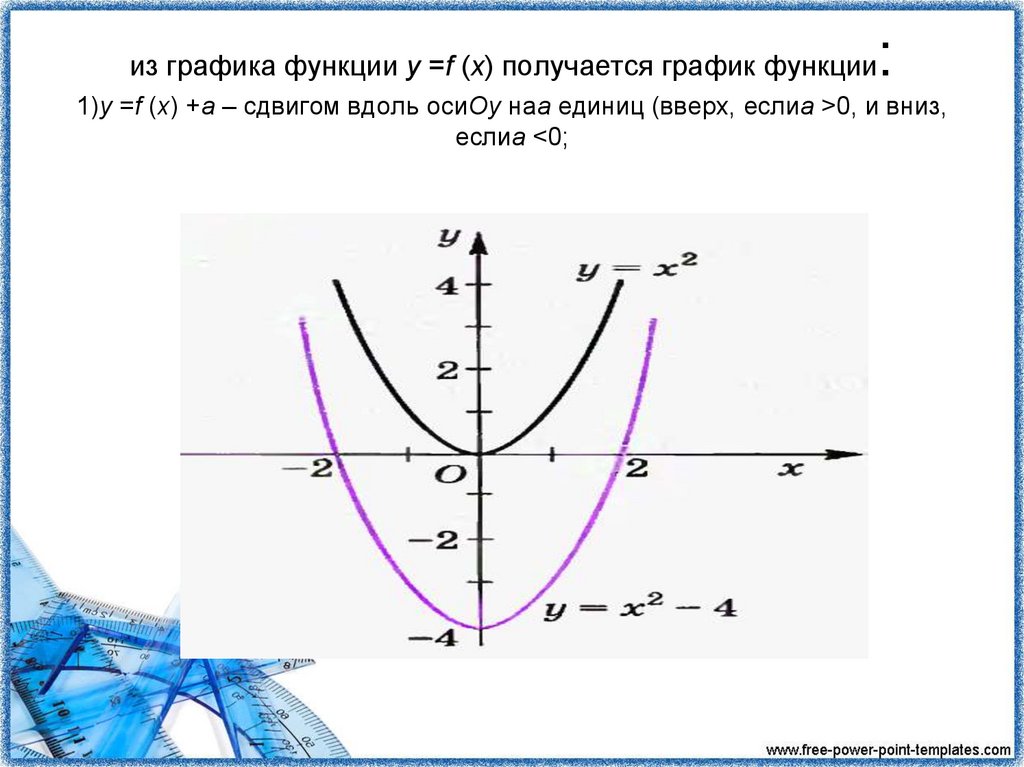
из графика функции y =f (x) получается график функции
1)y =f (x) +a – сдвигом вдоль осиOy наa единиц (вверх, еслиa >0, и вниз,
еслиa <0;

10. из графика функции y =f (x) получается график функции: 1)y =f (x) +a – сдвигом вдоль осиOy наa единиц (вверх, еслиa >0, и вниз,

:
из графика функции y =f (x) получается график функции
1)y =f (x) +a – сдвигом вдоль осиOy наa единиц (вверх, еслиa >0, и вниз,
еслиa <0;
2)y =f (x −b) – сдвигом вдоль осиOx наb единиц (вправо, еслиb >0 ,
ивлево, если b <0 ;

11. из графика функции y =f (x) получается график функции: 1)y =f (x) +a – сдвигом вдоль осиOy наa единиц (вверх, еслиa >0, и вниз,

:
из графика функции y =f (x) получается график функции
1)y =f (x) +a – сдвигом вдоль осиOy наa единиц (вверх, еслиa >0, и вниз,
еслиa <0;
2)y =f (x −b) – сдвигом вдоль осиOx наb единиц (вправо, еслиb >0 ,
ивлево, если b <0 ;
3)y =kf (x) – растяжением вдоль осиOy вk раз;

12. из графика функции y =f (x) получается график функции: 1)y =f (x) +a – сдвигом вдоль осиOy наa единиц (вверх, еслиa >0, и вниз,

:
из графика функции y =f (x) получается график функции
1)y =f (x) +a – сдвигом вдоль осиOy наa единиц (вверх, еслиa >0, и вниз,
еслиa <0;
2)y =f (x −b) – сдвигом вдоль осиOx наb единиц (вправо, еслиb >0 ,
ивлево, если b <0 ;
3)y =kf (x) – растяжением вдоль осиOy вk раз;
4)y =f (mx) – сжатием по осиOx вm раз;
.

13. из графика функции y =f (x) получается график функции: 1)y =f (x) +a – сдвигом вдоль осиOy наa единиц (вверх, еслиa >0, и вниз,

:
из графика функции y =f (x) получается график функции
1)y =f (x) +a – сдвигом вдоль осиOy наa единиц (вверх, еслиa >0, и вниз,
еслиa <0;
2)y =f (x −b) – сдвигом вдоль осиOx наb единиц (вправо, еслиb >0 ,
ивлево, если b <0 ;
3)y =kf (x) – растяжением вдоль осиOy вk раз;
4)y =f (mx) – сжатием по осиOx вm раз;
5)y = −f (x) – симметричным отражением относительно осиOx ;

14. из графика функции y =f (x) получается график функции: 1)y =f (x) +a – сдвигом вдоль осиOy наa единиц (вверх, еслиa >0, и вниз,

:
из графика функции y =f (x) получается график функции
1)y =f (x) +a – сдвигом вдоль осиOy наa единиц (вверх, еслиa >0, и вниз,
еслиa <0;
2)y =f (x −b) – сдвигом вдоль осиOx наb единиц (вправо, еслиb >0 ,
И влево, если b <0 ;
3)y =kf (x) – растяжением вдоль осиOy вk раз;
4)y =f (mx) – сжатием по осиOx вm раз;
5)y = −f (x) – симметричным отражением относительно осиOx ;
6)y =f (−x) – симметричным отражением относительно осиOy ;

15. из графика функции y =f (x) получается график функции: 1)y =f (x) +a – сдвигом вдоль осиOy наa единиц (вверх, еслиa >0, и вниз,

:
из графика функции y =f (x) получается график функции
1)y =f (x) +a – сдвигом вдоль осиOy наa единиц (вверх, еслиa >0, и вниз,
еслиa <0;
2)y =f (x −b) – сдвигом вдоль осиOx наb единиц (вправо, еслиb >0 ,
ивлево, если b <0 ;
3)y =kf (x) – растяжением вдоль осиOy вk раз;
4)y =f (mx) – сжатием по осиOx вm раз;
5)y = −f (x) – симметричным отражением относительно осиOx ;
6)y =f (−x) – симметричным отражением относительно осиOy ;
7)y =f (x) , следующим образом: часть графика, расположенная не
ниже оси Ox , остается без изменений, а «нижняя» часть графика
симметрично отражается относительно осиOx ;

16. из графика функции y =f (x) получается график функции: 1)y =f (x) +a – сдвигом вдоль осиOy наa единиц (вверх, еслиa >0, и вниз,

:
из графика функции y =f (x) получается график функции
1)y =f (x) +a – сдвигом вдоль осиOy наa единиц (вверх, еслиa >0, и вниз,
еслиa <0;
2)y =f (x −b) – сдвигом вдоль осиOx наb единиц (вправо, еслиb >0 ,
ивлево, если b <0 ;
3)y =kf (x) – растяжением вдоль осиOy вk раз;
4)y =f (mx) – сжатием по осиOx вm раз;
5)y = −f (x) – симметричным отражением относительно осиOx ;
6)y =f (−x) – симметричным отражением относительно осиOy ;
7)y =f (x) , следующим образом: часть графика, расположенная не
ниже оси Ox , остается без изменений, а «нижняя» часть графика
симметрично отражается относительно осиOx ;
8) y =|f ( x )|, следующим образом: правая часть графика (приx ≥0 )
остается без изменений, а вместо «левой» строится симметричное
отражение «правой» относительно оси Oy .

17. Этапы построения графика функции y = kf (m(x-b)) + a

y = f (x)
y = f (mx)
y = f (m(x-b))
y = kf (m(x-b))
y = kf (m(x-b)) + a

18. Построить графики функций

1) у = 1/2 sin (3x) – 2
2)
y = 2 3x+1 – 4
3)
y = 2 (x – 1)2 – 3
4) y = –3 log2(x + 1)

19. Итоги урока

Я знаю как……
Я умею ……..
Я смогу применить на практике……
Я достиг своей цели

20. Домашнее задание

• Стр. 28-30, разобрать п.5, № 1.70 (а-д).