Угол между прямой и плоскостью. Пирамида Хеопса

1. УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ

1

2. Пирамида Хеопса

2

3. Различаются тоннельные и поэтажные эскалаторы по углу наклона. Так, при требуемой высоте подъема до 6 метров угол наклона

эскалатора
составляет 30° или 35°,
при высоте подъема выше
6 метров — только 30°.
3

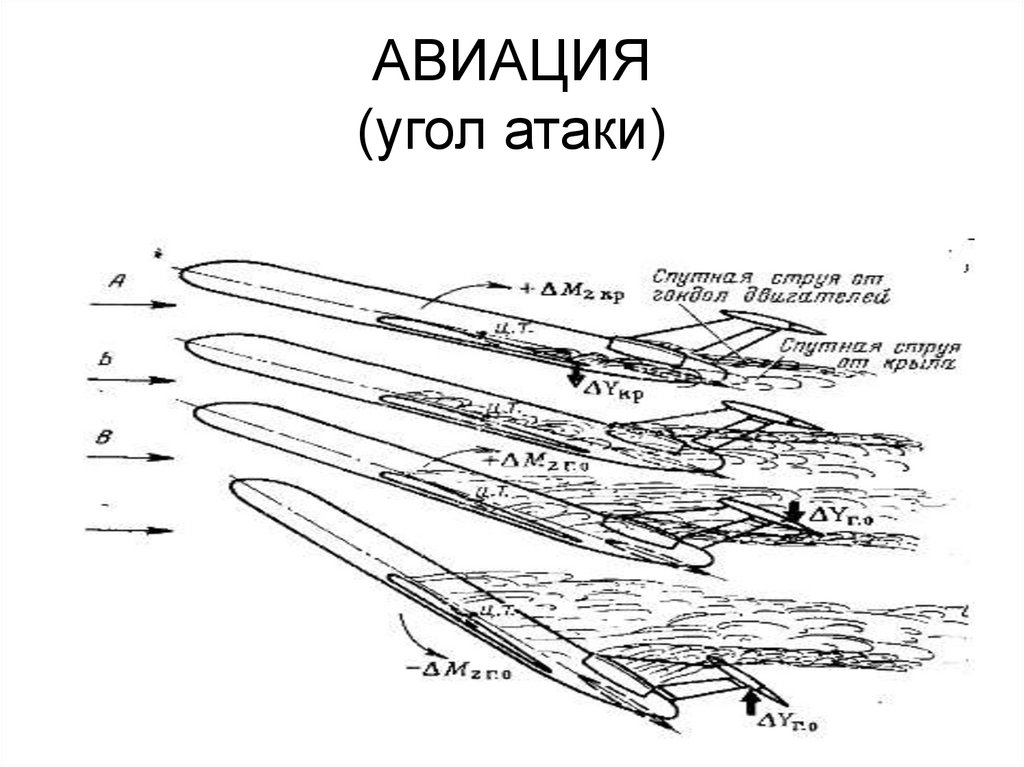
4. АВИАЦИЯ (угол атаки)

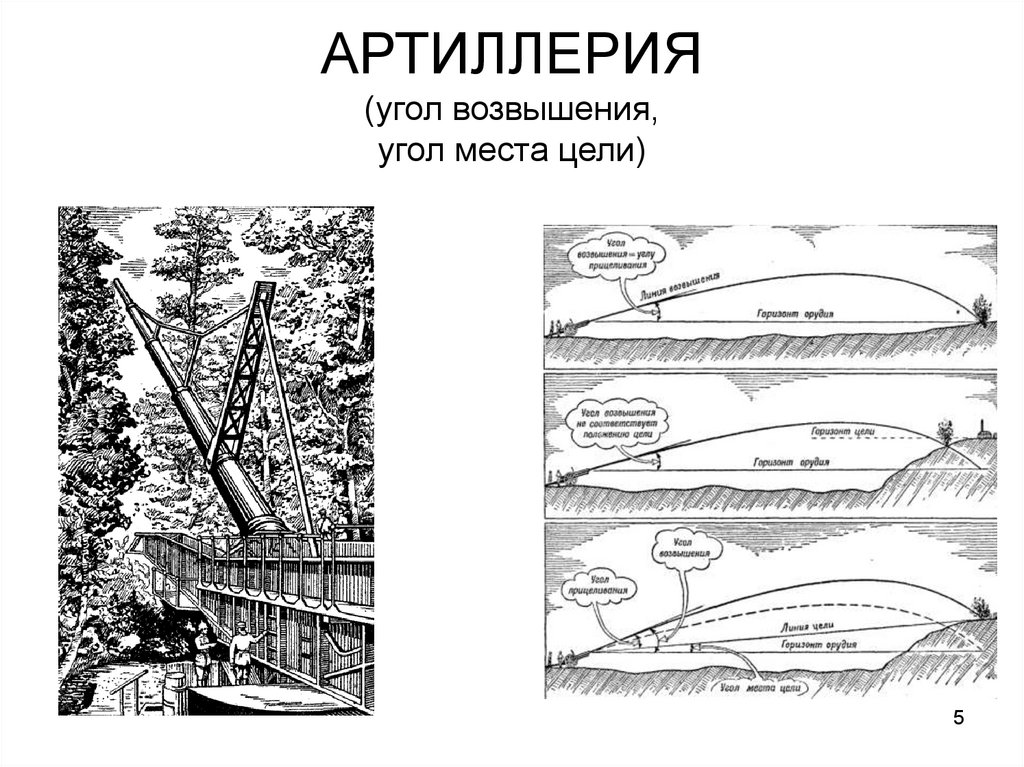
4

5. АРТИЛЛЕРИЯ (угол возвышения, угол места цели)

5

6. ЦЕЛЬ УРОКА

• Сформировать умение применять
понятие угла между прямой и
плоскостью к решению задач.
• Мы научимся строить такие углы и
решать вычислительные задачи,
используя данное понятие.
6

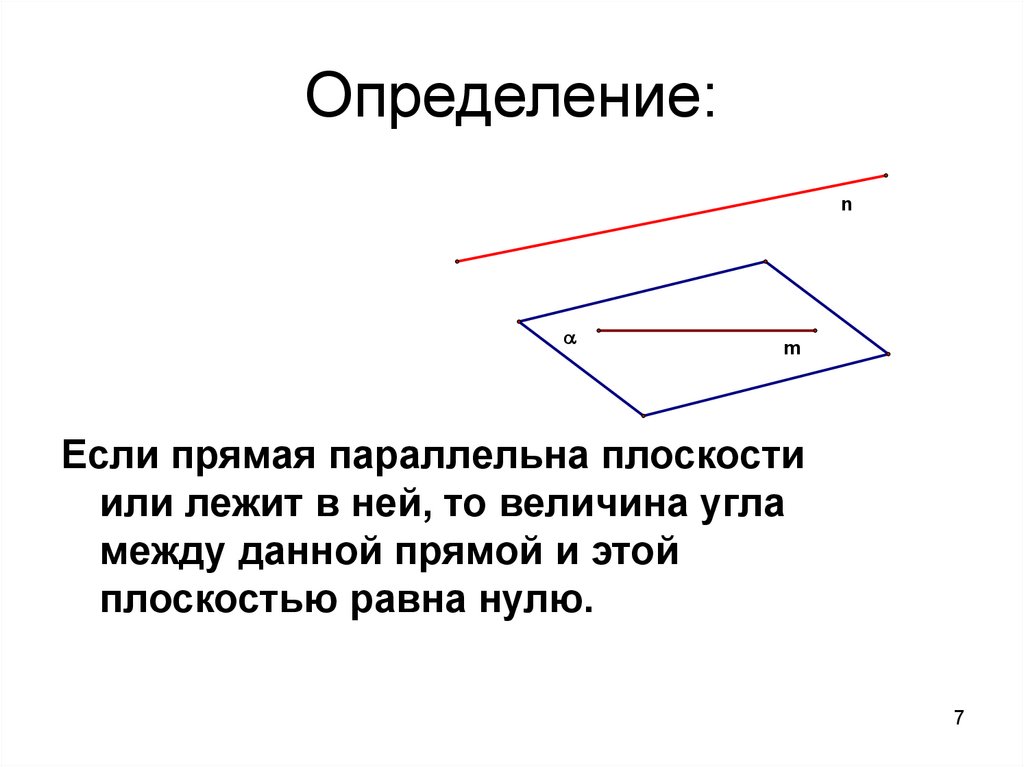
7. Определение:

n
m
Если прямая параллельна плоскости
или лежит в ней, то величина угла
между данной прямой и этой
плоскостью равна нулю.
7

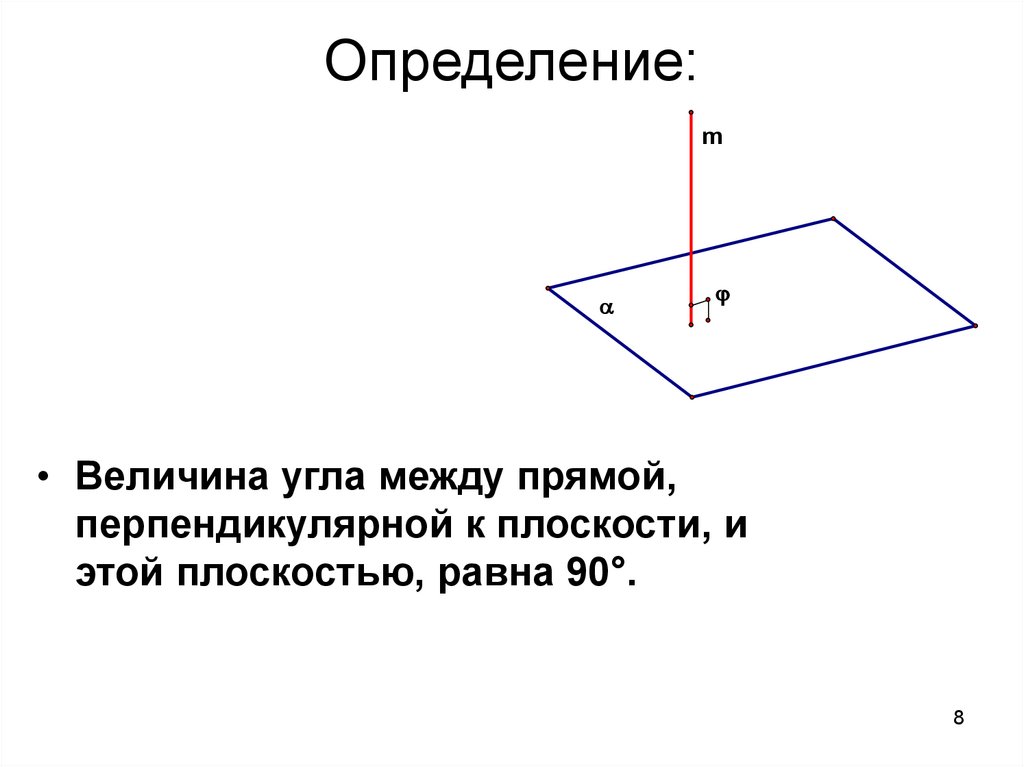
8. Определение:

m
• Величина угла между прямой,
перпендикулярной к плоскости, и
этой плоскостью, равна 90°.
8

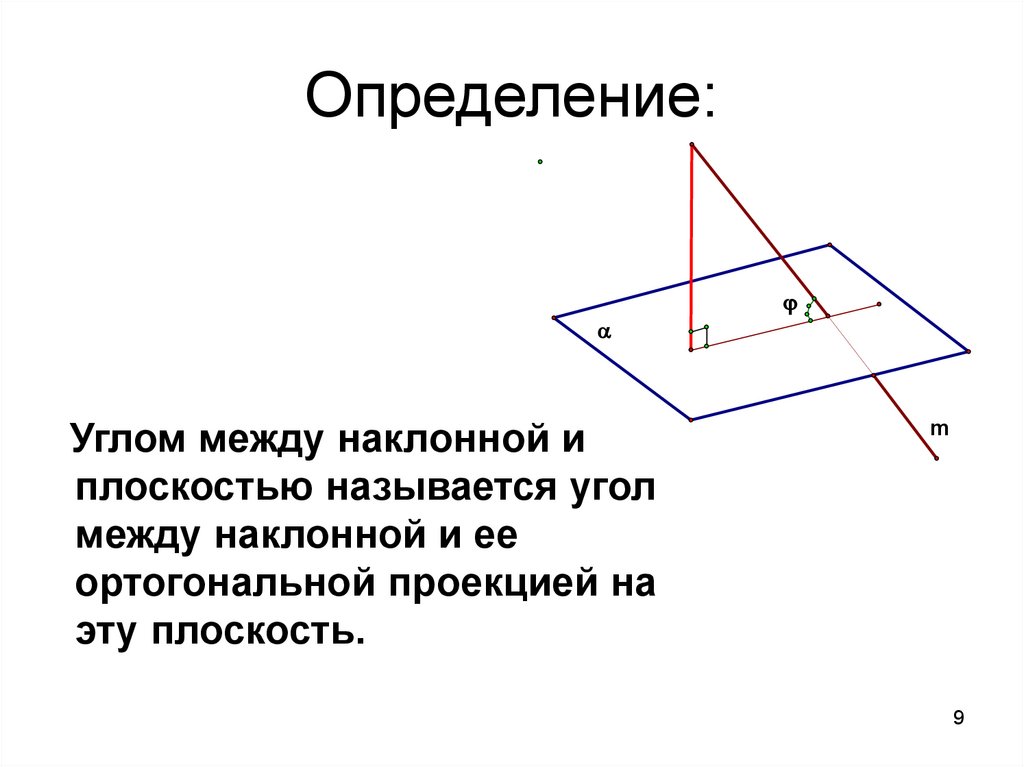
9. Определение:

Углом между наклонной и
плоскостью называется угол
между наклонной и ее
ортогональной проекцией на
эту плоскость.
m
9

10.

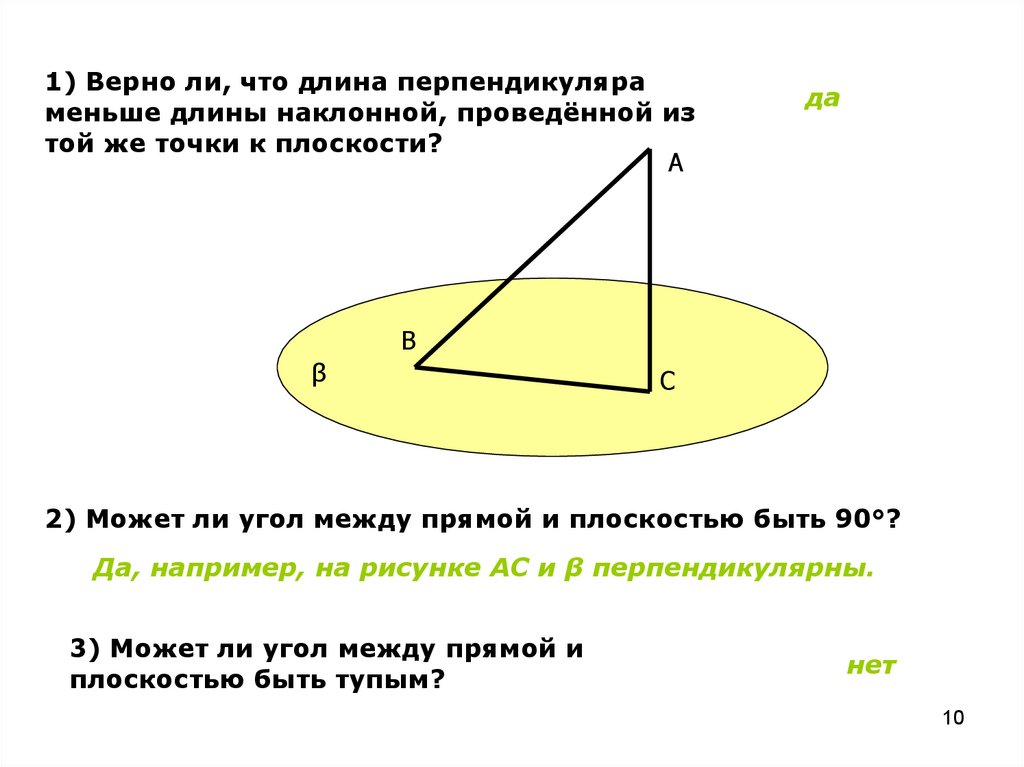
1) Верно ли, что длина перпендикуляра
меньше длины наклонной, проведённой из
той же точки к плоскости?
А
да
В
β
С
2) Может ли угол между прямой и плоскостью быть 90°?
Да, например, на рисунке АС и β перпендикулярны.
3) Может ли угол между прямой и
плоскостью быть тупым?
нет
10

11.

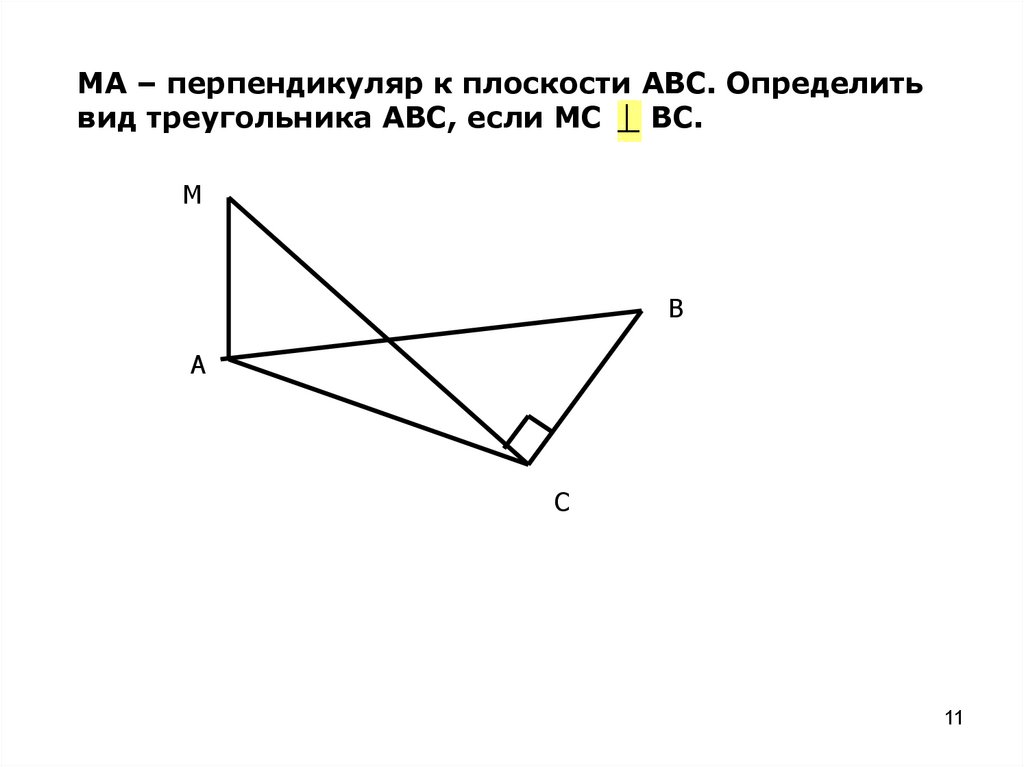
МА – перпендикуляр к плоскости АВС. Определить
вид треугольника АВС, если МС
ВС.
М
В
А
С
11

12.

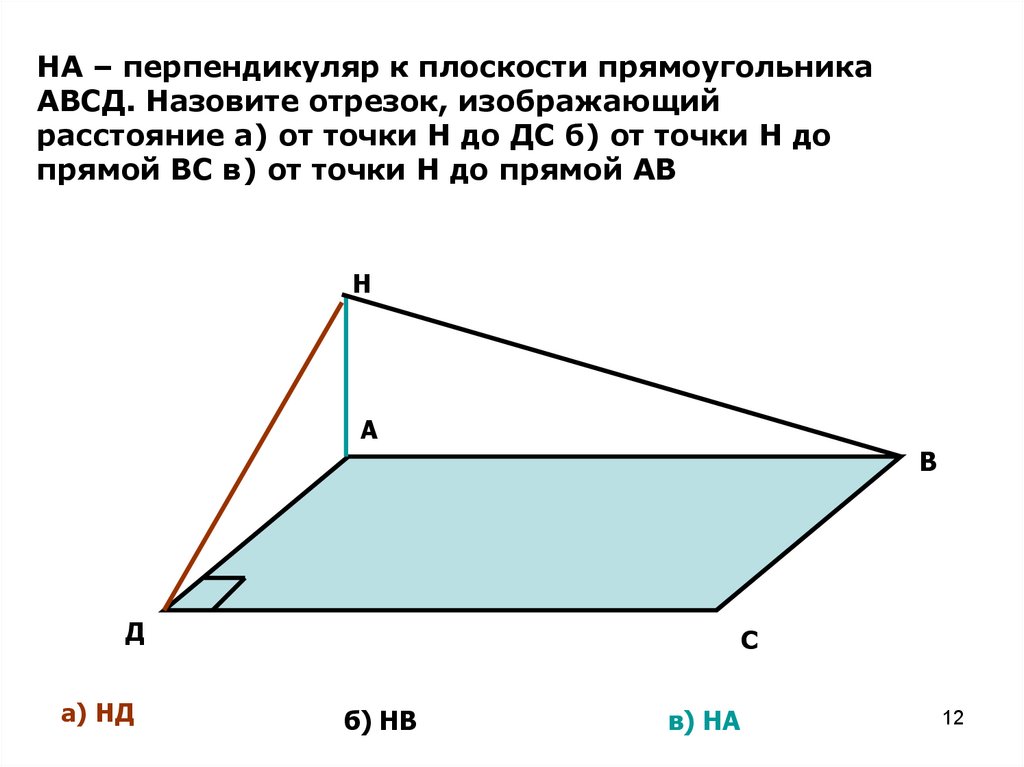
НА – перпендикуляр к плоскости прямоугольника
АВСД. Назовите отрезок, изображающий
расстояние а) от точки Н до ДС б) от точки Н до
прямой ВС в) от точки Н до прямой АВ
Н
А
В
Д
а) НД
С
б) НВ
в) НА
12

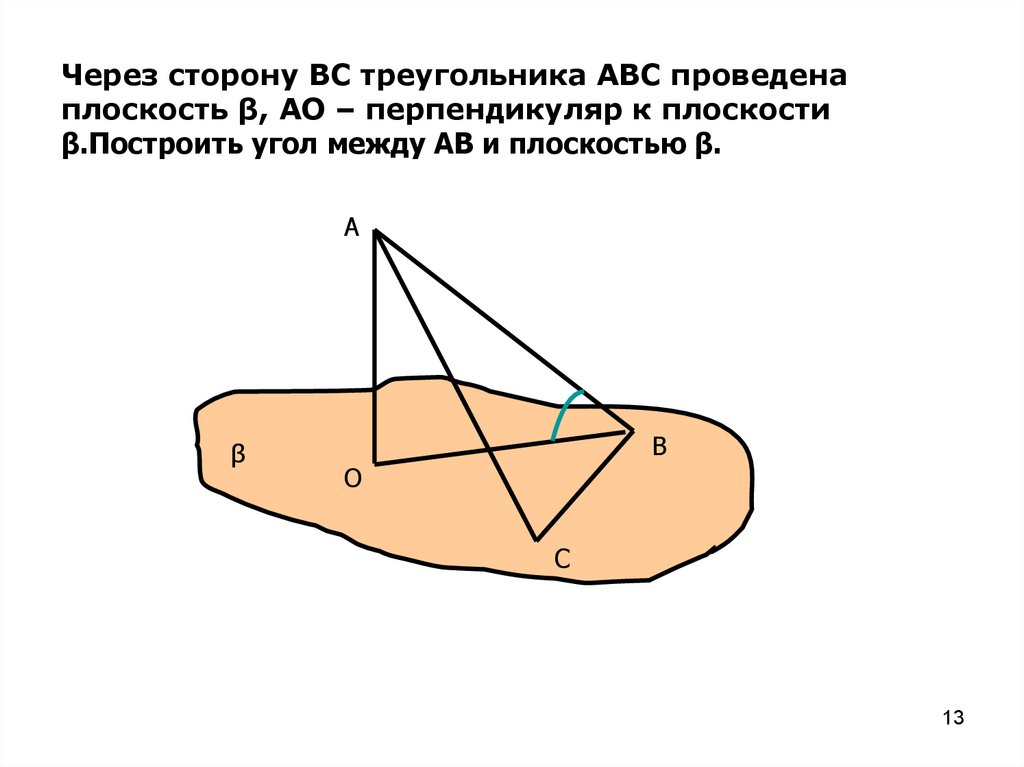
13.

Через сторону ВС треугольника АВС проведена
плоскость β, АО – перпендикуляр к плоскости
β.Построить угол между АВ и плоскостью β.
А
β
В
О
С
13

14.

Точка О – точка пересечения диагоналей ромба АВСД, КВ
– перпендикуляр к плоскости АВС. Построить отрезок,
изображающий расстояние от точки К до прямой АС.
К
С
В
О
А
Д
ВО
АС, ВО – проекция КО на АВС, значит КО
расстояние от К до АС.
АС, значит КО -
14

15.

ОПРОС
1. Сформулировать определение
перпендикулярных прямой и
плоскости.
15

16.

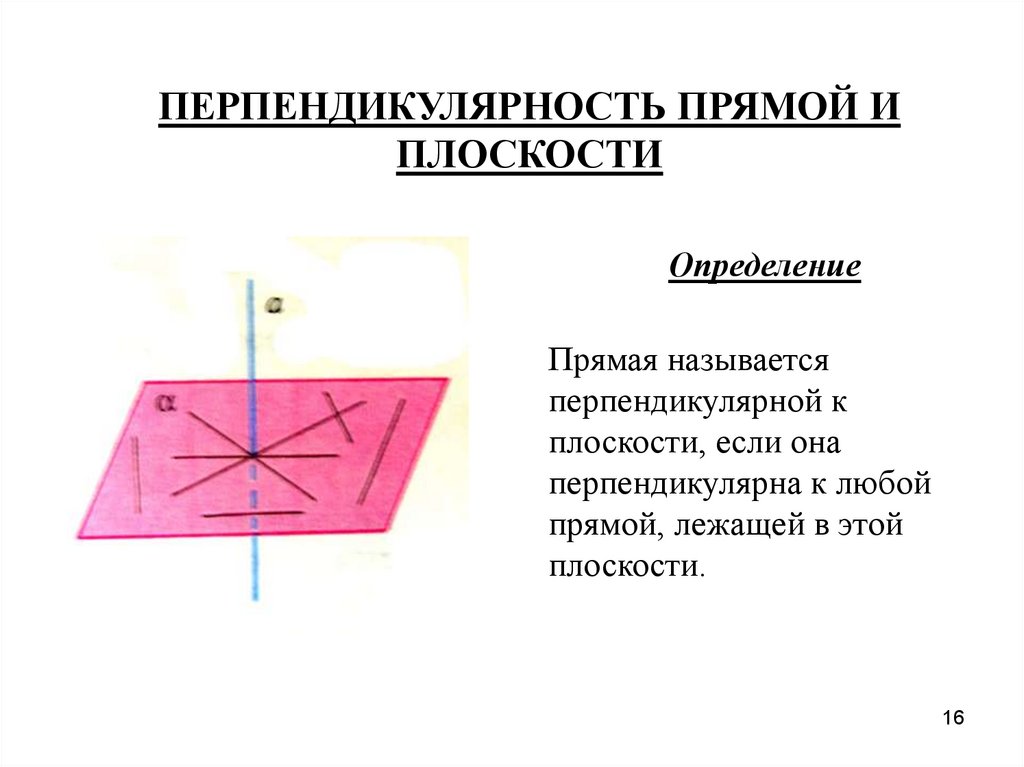
ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И
ПЛОСКОСТИ
Определение
Прямая называется
перпендикулярной к
плоскости, если она
перпендикулярна к любой
прямой, лежащей в этой
плоскости.
16

17.

ОПРОС
2. Сформулировать признак
перпендикулярности прямой и
плоскости.
17

18.

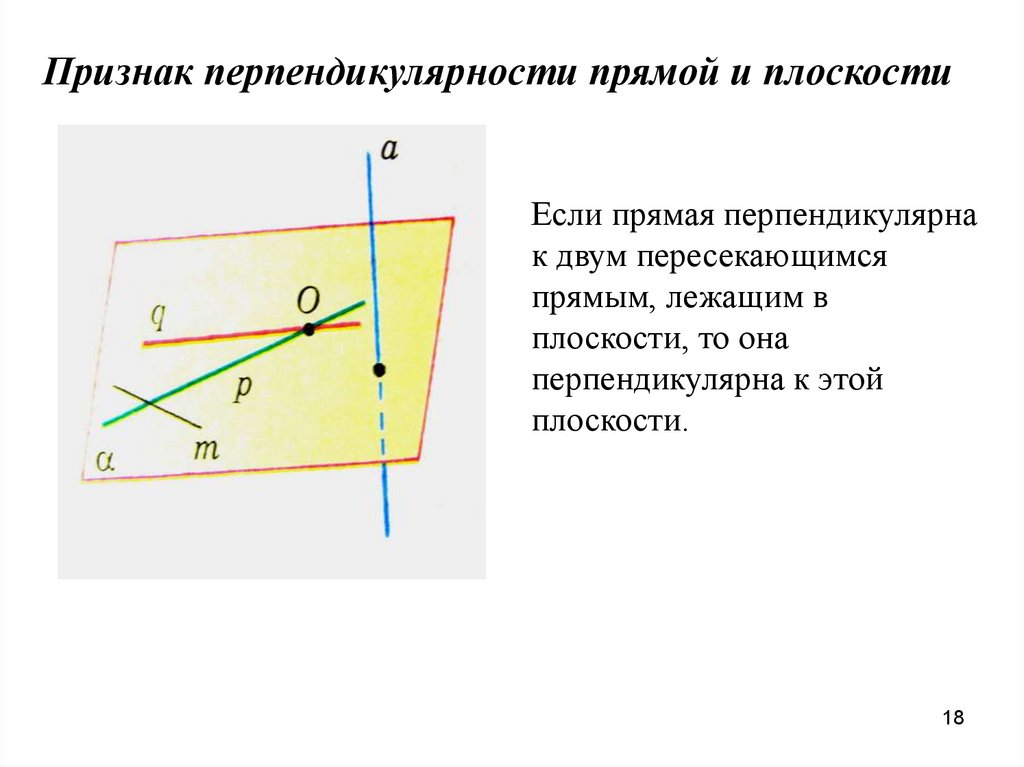
Признак перпендикулярности прямой и плоскости
Если прямая перпендикулярна
к двум пересекающимся
прямым, лежащим в
плоскости, то она
перпендикулярна к этой
плоскости.
18

19.

ОПРОС
3. Сформулировать теорему о трёх
перпендикулярах.
19

20.

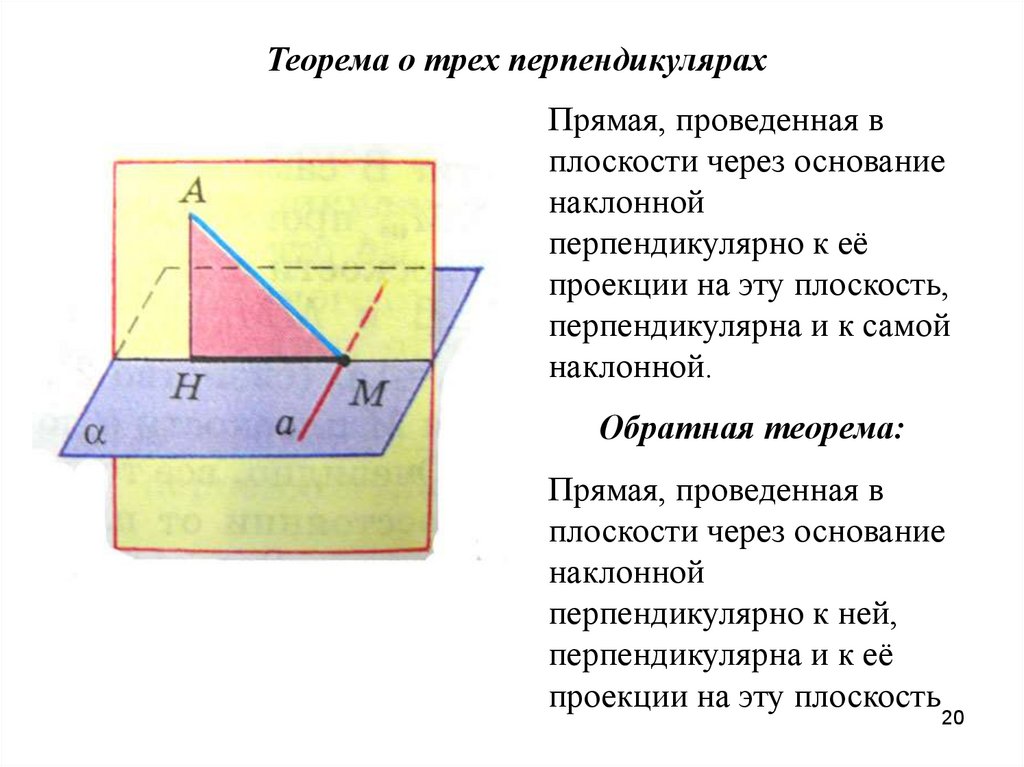
Теорема о трех перпендикулярах
Прямая, проведенная в
плоскости через основание
наклонной
перпендикулярно к её
проекции на эту плоскость,
перпендикулярна и к самой
наклонной.
Обратная теорема:
Прямая, проведенная в
плоскости через основание
наклонной
перпендикулярно к ней,
перпендикулярна и к её
проекции на эту плоскость
20

21.

ОПРОС
4. Дать определение угла
между прямой и плоскостью.
21

22.

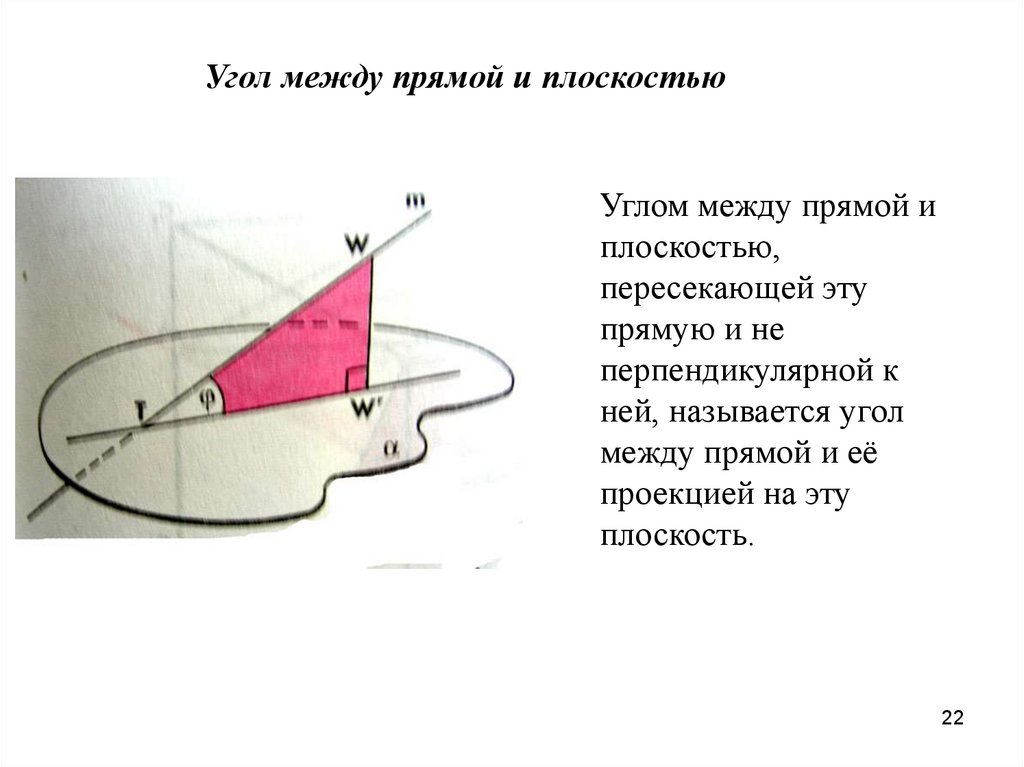
Угол между прямой и плоскостью
Углом между прямой и
плоскостью,
пересекающей эту
прямую и не
перпендикулярной к
ней, называется угол
между прямой и её
проекцией на эту
плоскость.
22

23.

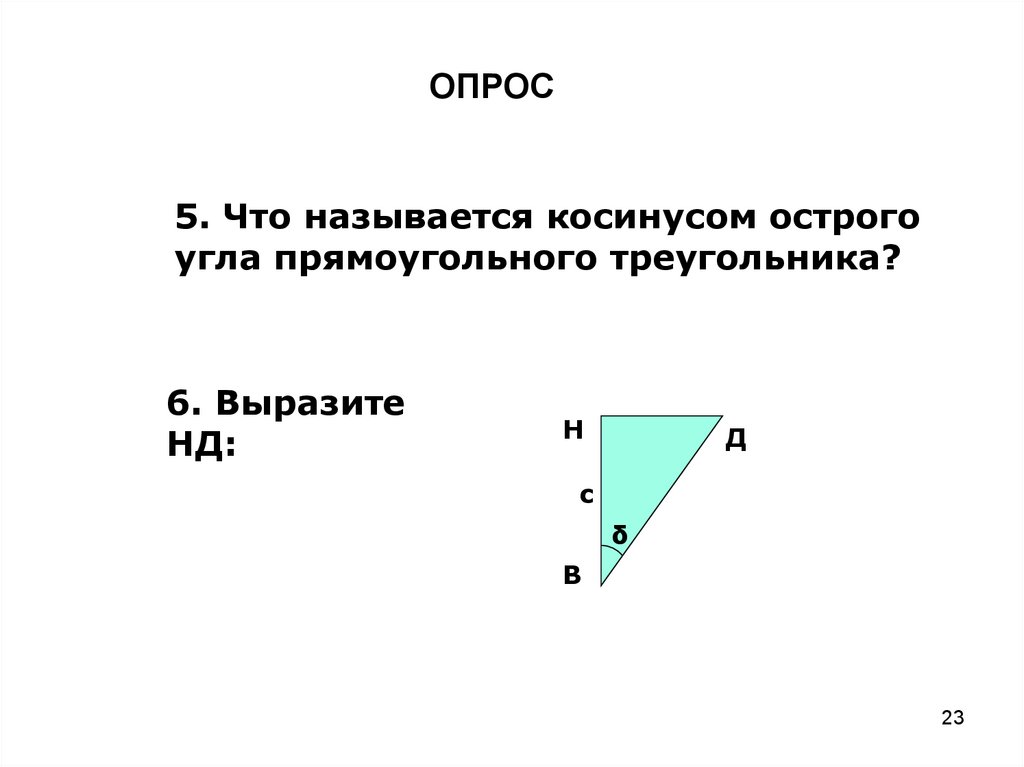
ОПРОС
5. Что называется косинусом острого
угла прямоугольного треугольника?
6. Выразите
НД:
Н
Д
с
δ
В
23

24.

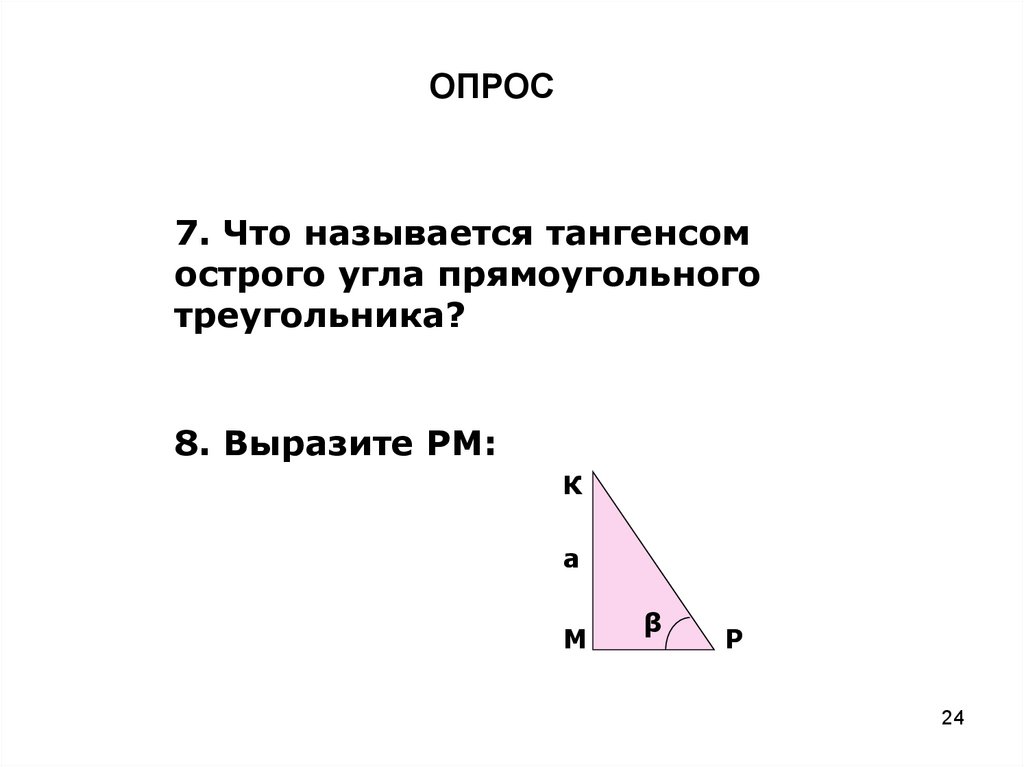
ОПРОС
7. Что называется тангенсом
острого угла прямоугольного
треугольника?
8. Выразите РМ:
К
а
М
β
Р
24

25. АЛГОРИТМ НАХОЖДЕНИЯ УГЛА

1. Построение проекции прямой на
плоскость.
• 2. Нахождение угла между прямой и ее
проекцией на плоскость.
25

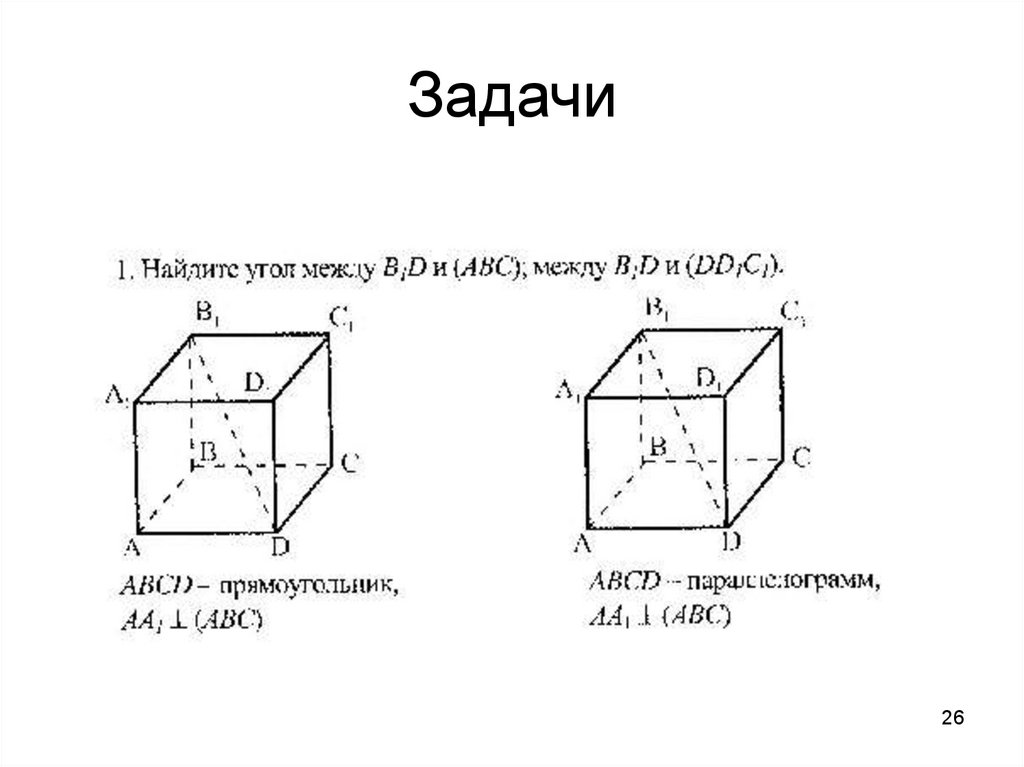
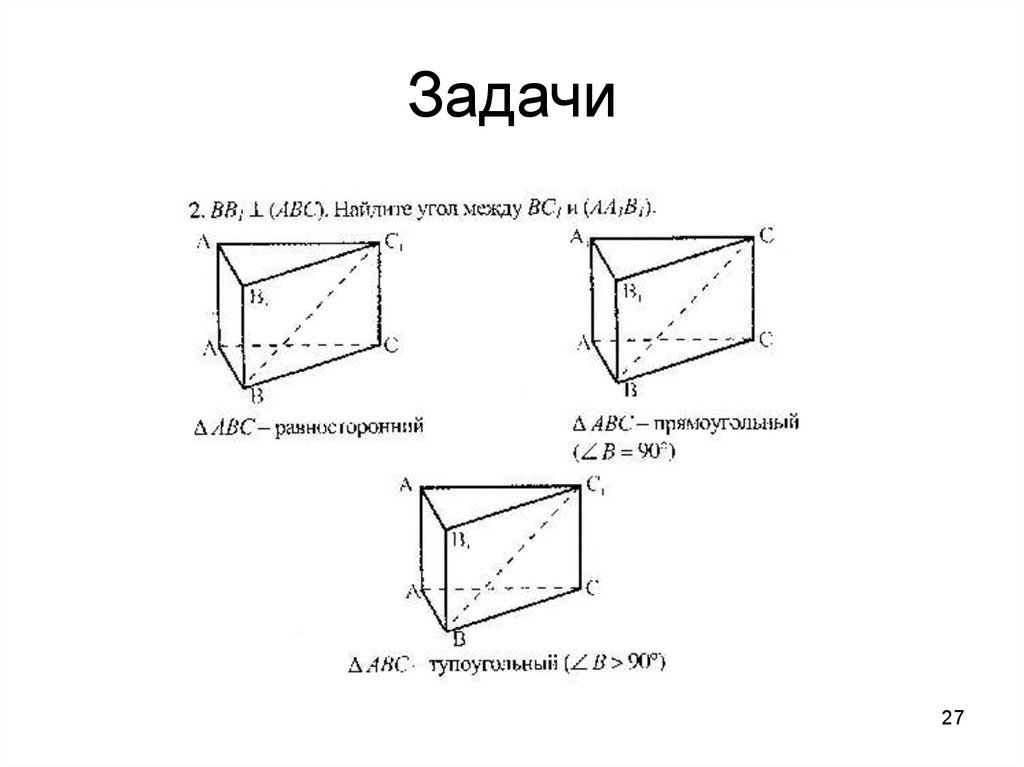
26. Задачи

26

27. Задачи

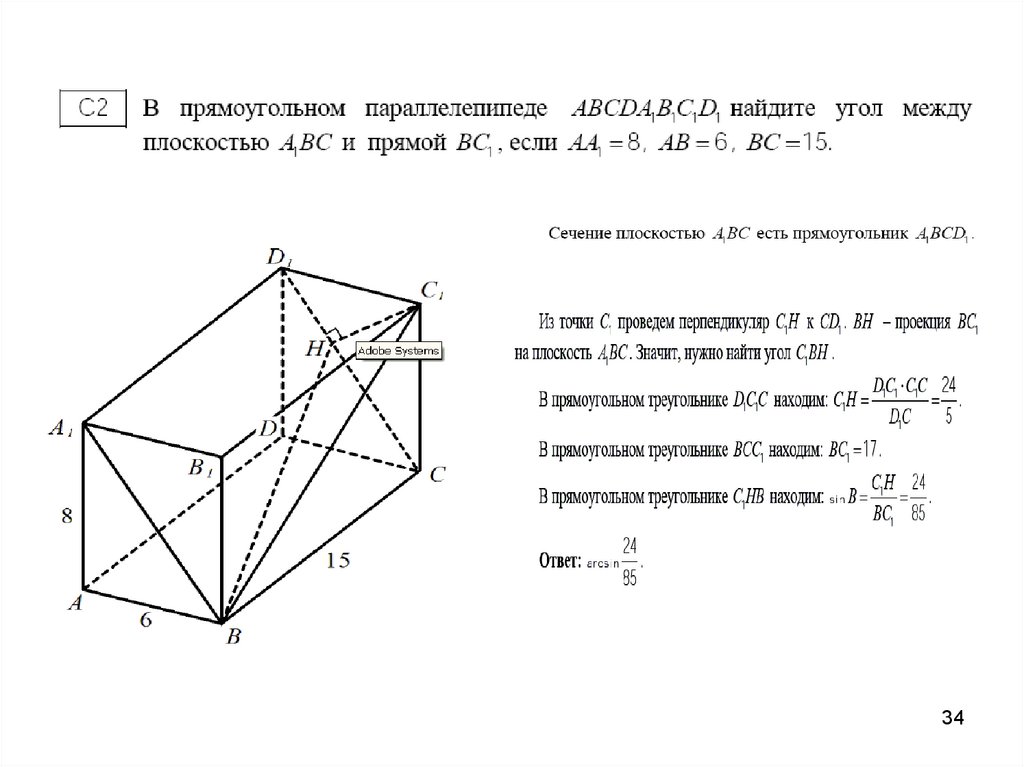
27

28. ЗАДАЧИ ИЗ ЕГЭ

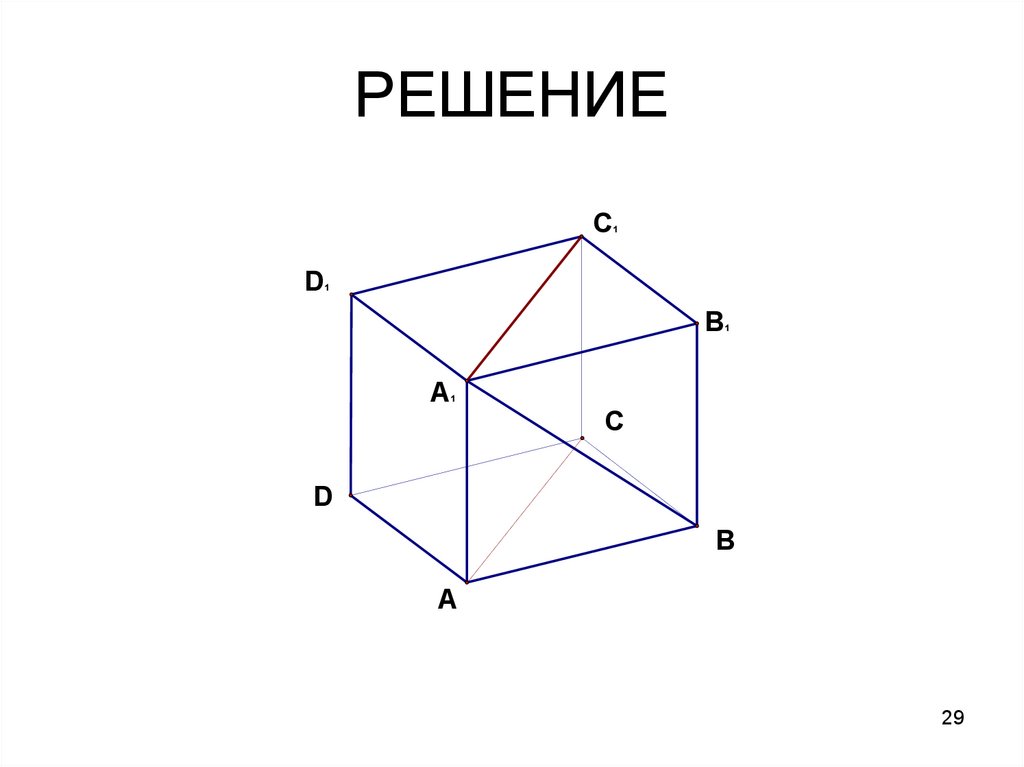
28

29. РЕШЕНИЕ

C
D
1
1
B
A
1
1
C
D
B
A
29

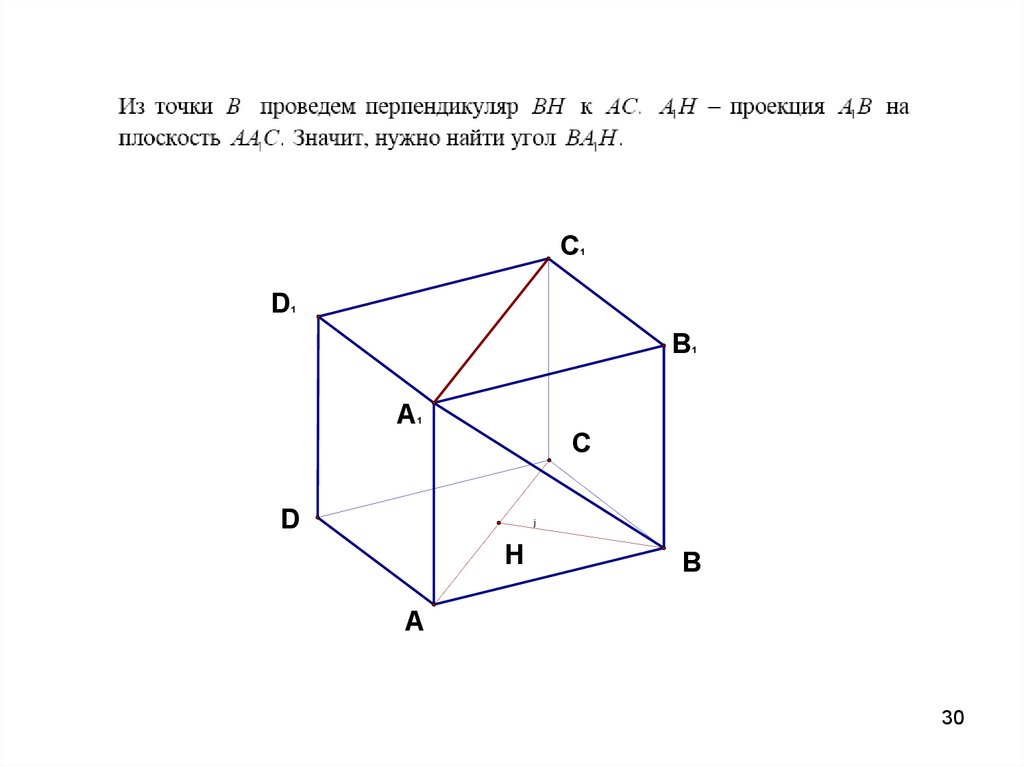
30.

C
D
1
1
B
A
1
1
C
D
j
H
B
A
30

31.

C
D
1
1
B
A
1
1
C
D
j
H
B
A
31

32. Задача 1:

Из точки проведены к плоскости две
наклонные, образующие с
плоскостью углы в 30°.
Найти расстояние между точками
пересечения наклонных с
плоскостью, если расстояние от
исходной точки до плоскости равно
10, а угол между проекциями
наклонных равен 120°.
32

33. Задача 2:

В треугольнике ABC угол C - прямой,
AB=36, гипотенуза составляет угол 60°
с плоскостью, содержащей AC. Какова
наибольшая возможная длина AC ?
33

34.

34